목차
이전까지 대표적인 생성모델인 AutoRegressive Models(ARMs), Flow-based models, Variational Auto-Encoders (VAEs), Generative Adversarial Networks(GANs)를 살펴보았다. 이번 글에서는 최근에 diffusion-based models와 함께 관심을 끌고 있는 score-based model에 대해 알아보려 한다.
사실 score-based model이 처음 제안된 시기는 2019년(Generative Modeling by Estimating Gradients of the Data Distribution, NeurIPS), 2021년(Score-based Generative Modeling through Stochastic Differential Equations, ICLR)으로 diffusion(2015년 Deep Unsupervised Learning using Nonequilibrium Thermodynamics, ICML, 2020년 Denoising Diffusion Probabilistic Models, NeurIPS)보다 늦지만, 개인적으로 diffusion에 가장 관심이 있기도 하고, diffusion을 이해하는 방법 중에 score-based model을 이해해야 하는 부분이 있어 먼저 다뤄보고, 마지막으로 diffusion을 다뤄볼 것이다.
참고한 블로그 글은 아래와 같다.
https://yang-song.net/blog/2021/score/
Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song
Generative Modeling by Estimating Gradients of the Data Distribution This blog post focuses on a promising new direction for generative modeling. We can learn score functions (gradients of log probability density functions) on a large number of noise-pertu
yang-song.net
Generative Modeling Techniques

이제까지 알아본 generative model 중, 최근까지도 자주 사용되는 모델은 Fig 1과 같다. 생성모델을 크게 나누면 likelihood를 사용하는지, 아닌지에 따라 다음과 같이 나눠볼 수 있다.
Likelihood-based models

Likelihood-based models는 Data의 distribution을 직접 모델링하여 학습한다. 이에는 ARMs(AutoRegressive Models), Normalizing flows(Flow-based models), EBMs(Energy-Based Models), 그리고 VAEs(Variational AutoEncoders)가 포함된다.
이러한 생성모델의 한계점은 엄격한 restriction이 필요하거나, likelihood를 근사하기 위한 objective에 의존적이라는 것이다.
Implicit models

Implicit models는 모델이 샘플링 과정에서 data의 probability distribution을 implicit하게 표현한다. 이에는 GANs (Generative Adversarial Networks)가 대표적이다.
이 모델은 Adversarial training으로 인해 학습이 불안정하고, mode collapse 문제가 발생하기 쉽다.
Score-based models
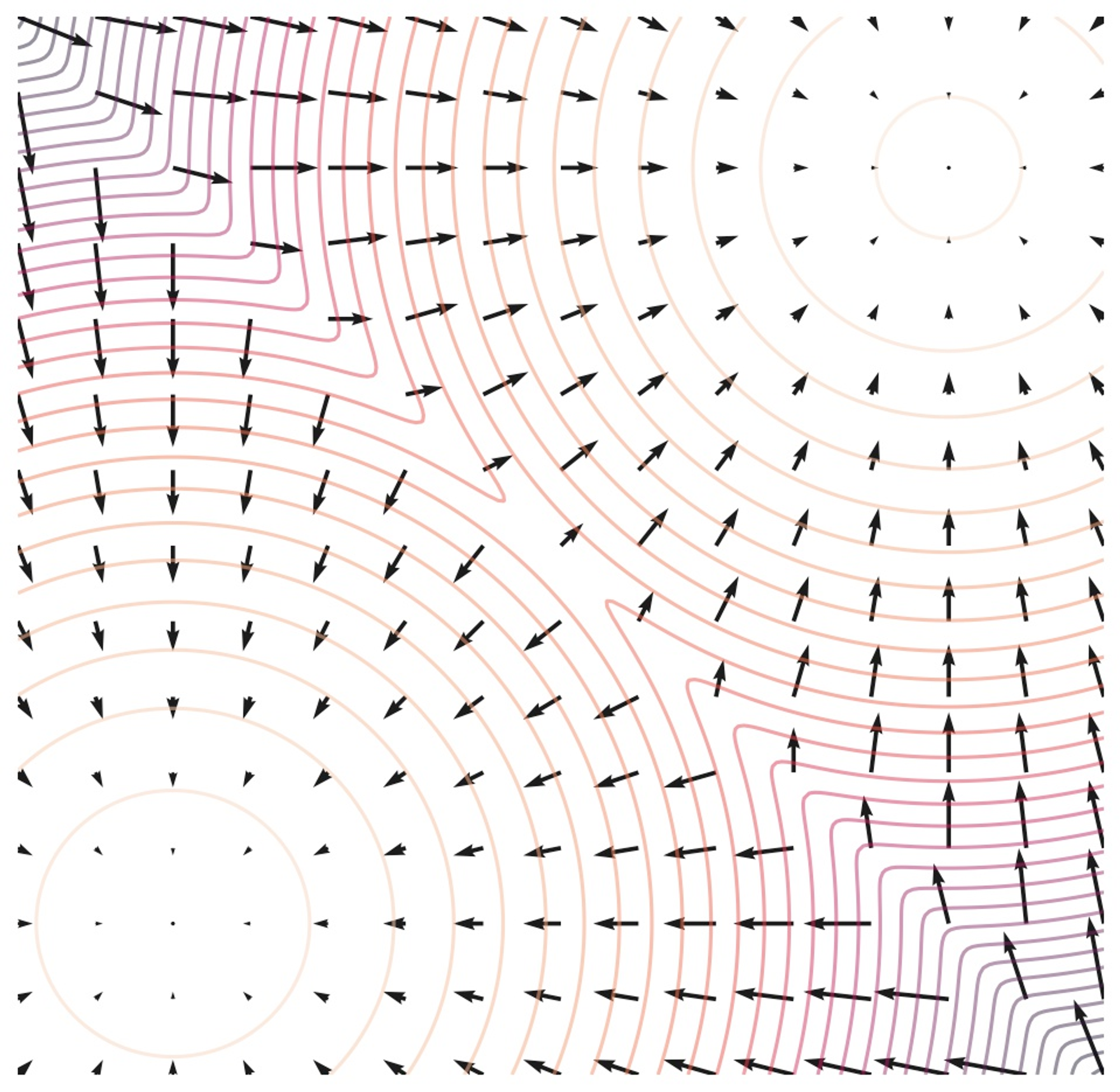
위 두 유형과 달리, 이번 글에서 다룰 score-based model은 score function을 modeling 및 estimating하면서 여러 generative task에 적용한다.
Likelihood 기반 모델과 달리 계산 가능한 normalizing constant가 필요 없으며, adversarial loss에 비해 안정적인 score matching이라는 방법으로 학습한다. 또한, Normalizing flow model과 연관이 있어 정확한 likelihood 계산과 representation learning이 가능하다.
Score Function, Score-based Models, and Score Matching
주어진 데이터셋
이때 probability density function (pdf)는 다음과 같이 정의한다.
- Unnormalized probabilistic model(energy-based model)
그리고 이러한 모델은 maximum log-likelihood로 학습한다.
이때, pdf curve 아래 면적의 합은 항상 1
Score-based model
이 모델의 objective는
PDF를 정의할 때 등장했던 energy-based model
이 과정에서 constant가 미분 과정에서 소거되므로, VAE 등에서 계산이 불가능했던 원흉인 normalizing constant
Score-based model을 학습할 때에는 model과 data distribution 사이의 Fisher divergence를 활용한다.
Fisher divergence는 GT data score와 score-based model의 예측 값 간의 L2 거리 개념이다.
Data score
Score matching object는 dataset 기반으로 추정이 가능하며 stochastic graident descent로 최적화할 수 있다. 이는 normalizing constant를 알고 있는 상태에서의 log-likelihood based model들의 objective와 같다.
Langevin Dynamics
Langevin Dynamics는 Fig 5와 같이 학습된 score-based model

이 방법은 iterative하게 작동하며, Markov Chain Monte Carlo (MCMC) procedure를 사용한다.
- Initialization
이 과정에서 Regularization을 적용하면, 과정이 반복될수록(
Score-based Generative Modeling
Naive (Unconditional) Score-based Generative Modeling
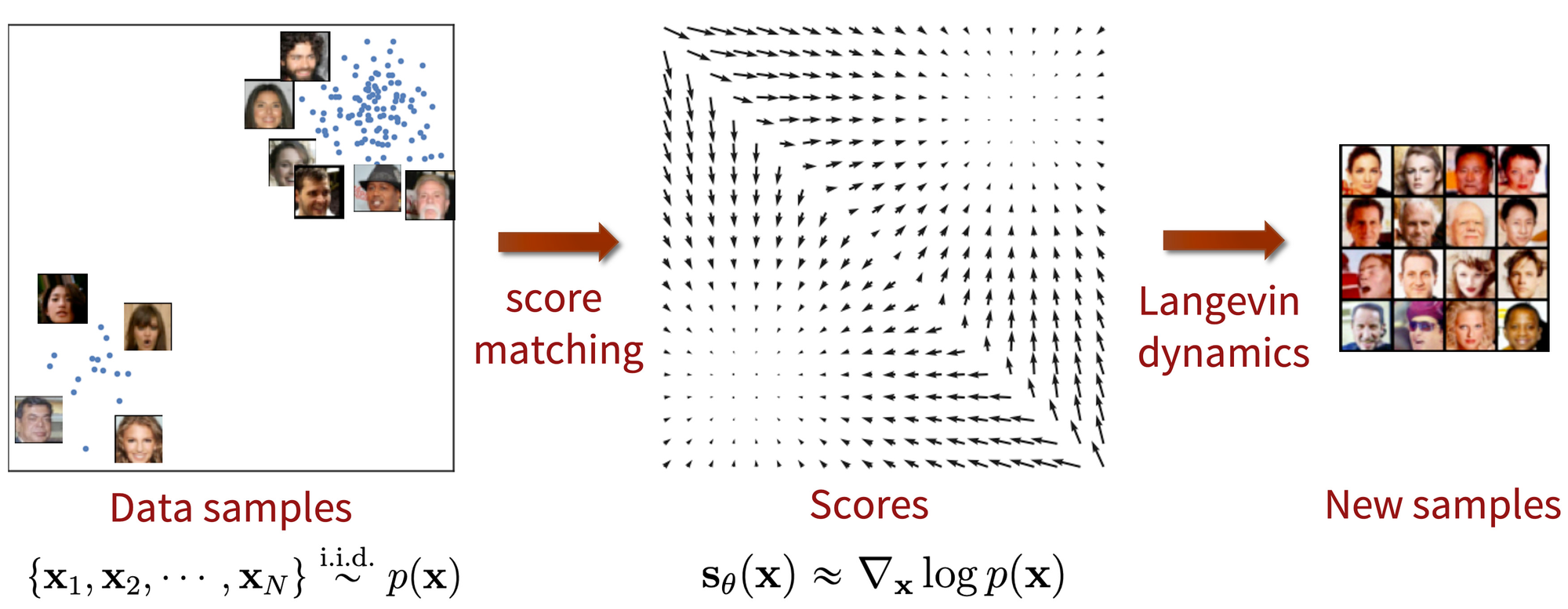
이 모델은 Fig 6과 같이 score matching으로 학습을, Langevin dynamics를 활용하여 샘플링을 수행한다.
그러나 한계점이 있는데, low density 지역(data point가 많이 없는 지역)에서 추정한 score function이 부정확하다는 것이다.
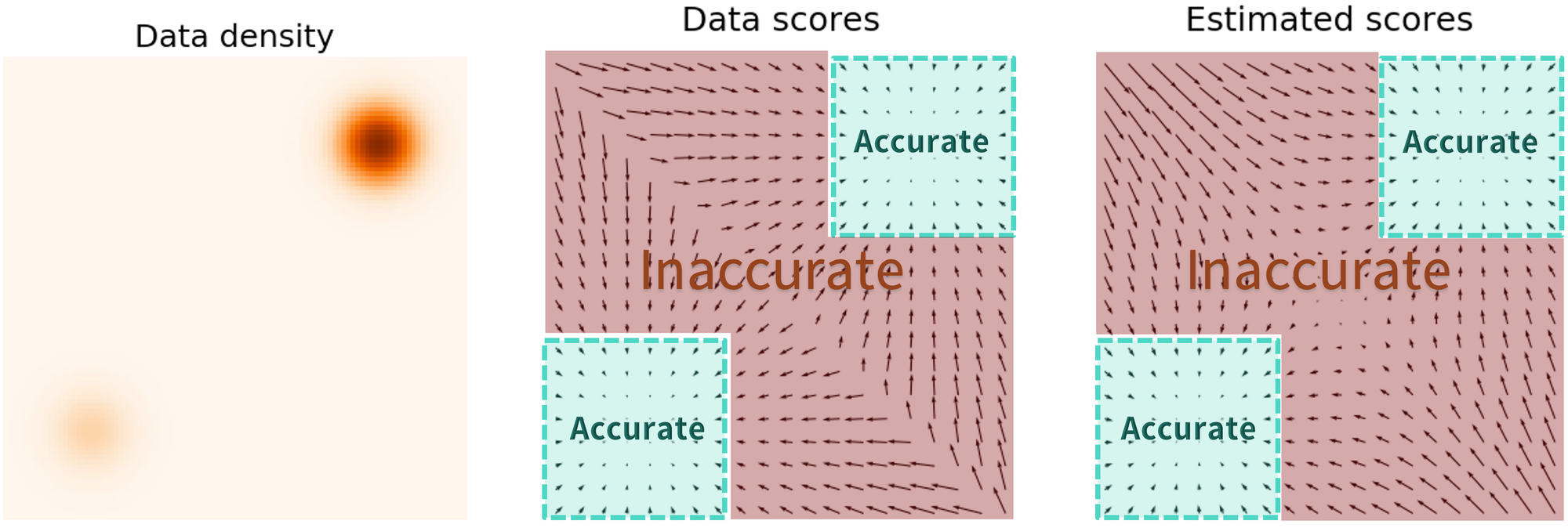
Objective를 보면 그 이유를 알 수 있다.
우변을 보면, L2 difference에
이 문제를 해결하기 위해 Noise perturbation을 사용한다.
Score-based Generative Modeling with Multiple Noise Perturbations
Noise perturbation이란, data point에 perturbation을 적용한 후 score-based model을 학습하는 방법이다. 이 방법을 사용한 score-based model을 noise conditional score-based model

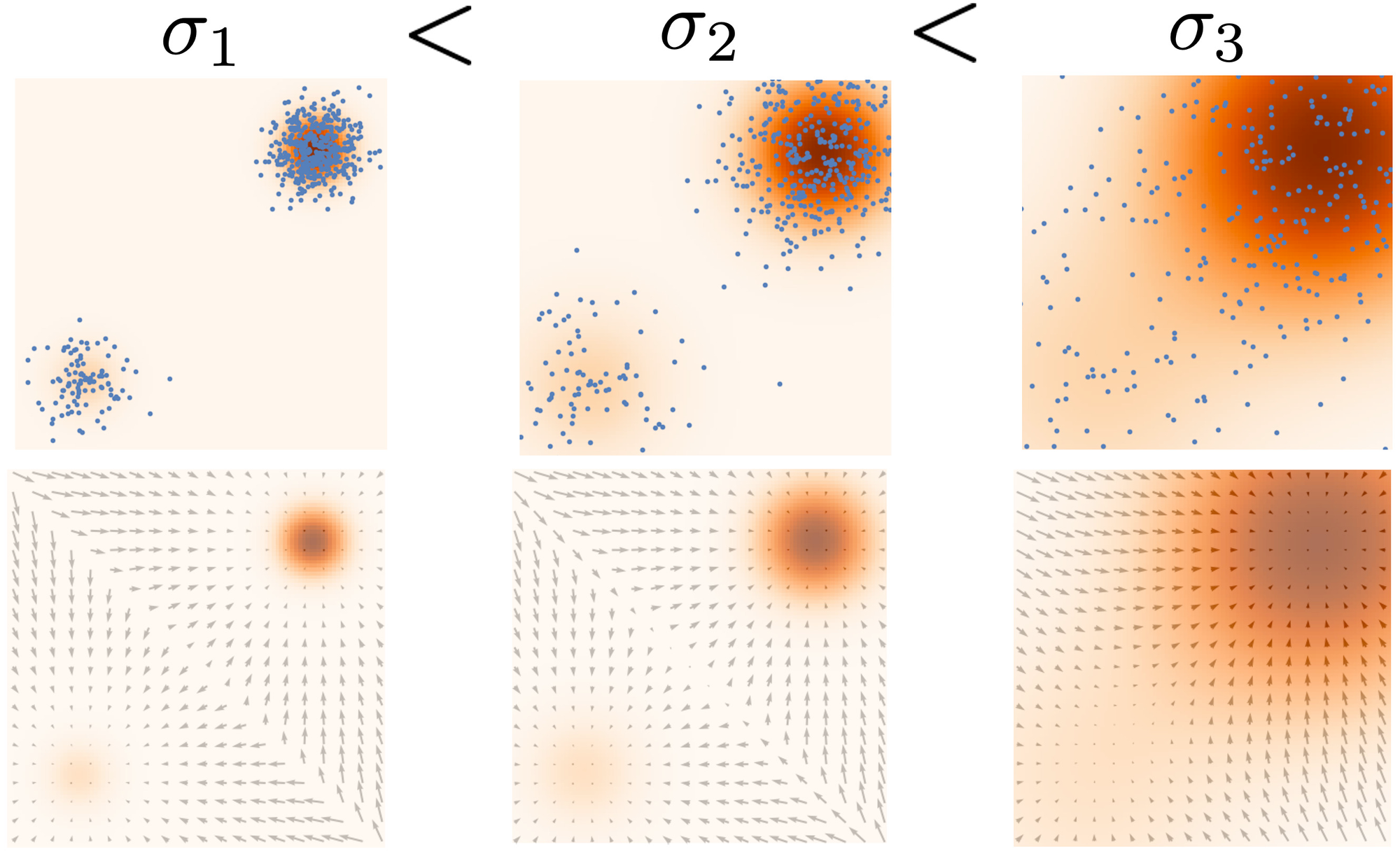
Fig 8에서와 같이, perturbation을 적용하면 data point의 분포가 더 퍼지게 되어 기존의 문제를 해결할 수 있게 된다. 하지만, perturbation을 얼마나 줄 것인가(noise의 scale)가 문제인데, 여러 scale의 noise를 동시에 적용하는 Multiple noise perturbation을 사용한다. (
- Multiple Gaussian noise
샘플링 할 때는
Score matching (Training) of noise conditional score-based model
이 모델의 training objective는 모든 noise
Annealed Langevin dynamics (Sampling) of noise conditional score-based model
샘플링 할 때에는 noise-conditional score-based model

Fig 10과 같이, 샘플링을 진행할수록 점점 noise가 사라진다. (이는 diffusion에서 time step에 따라 denoising되는 것과 비슷하다!)
NCSN Implementation
- Score-based model
- Test 시 model의 weight에 exponential moving average를 적용한다.
Score-based generative modeling with Stochastic Differential Equations (SDEs)
Multiple noise를 일반화하여 scale 개수를 무한히 늘린다. 이러한 모델을 time-dependent score-based model
이를 통해 샘플 퀄리티를 높이고, 정확한 log-likelihood를 계산할 수 있으며, controllable generation이 가능하다. 이는 diffusion의 forward process 및 reverse process와 같은 개념이 된다. Diffusion 내용은다음 글에서 따로 다룰 것이다.
Perturbing data with an SDE (Training)
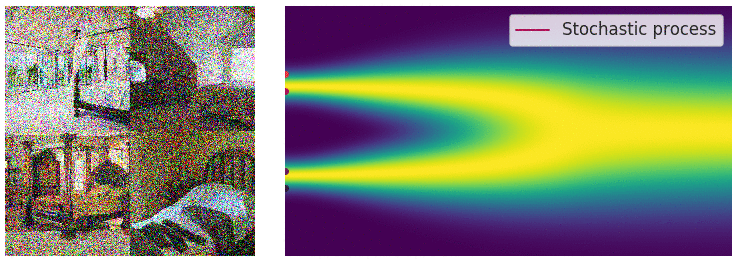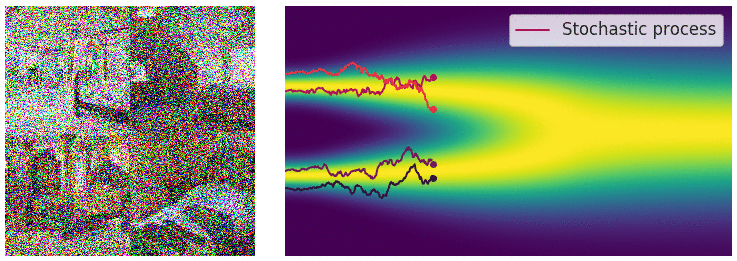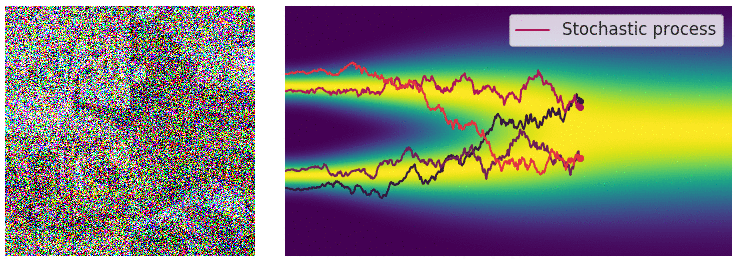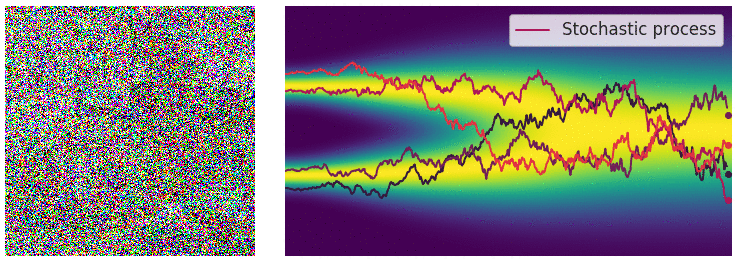
Data에 무수히 많은 noise를 가하는 과정을 SDE process라 하고, SDE의 해를 구하는 과정이다. 이는 Fig 11과 같이 diffusion process를 연상시킨다.
- 해 : Random variables의 continuous collection
- Random variable
- Random variable
SDE는 다양하게 설정할 수 있다. 예를 들어,
Training objective는 다음과 같이 Fisher divergence에 time step
- 보통
- 보통
이전에 알아본 noise scale 개수가 유한할 때와 비교해보자면,
Reversing the SDE for sample generation
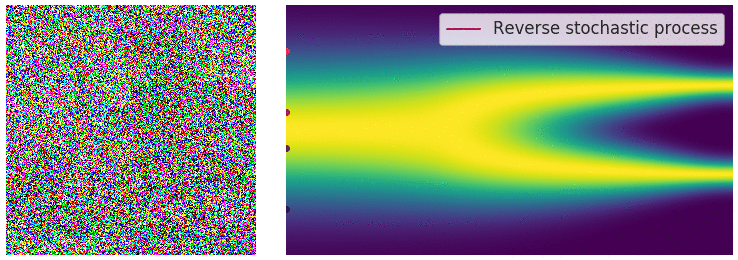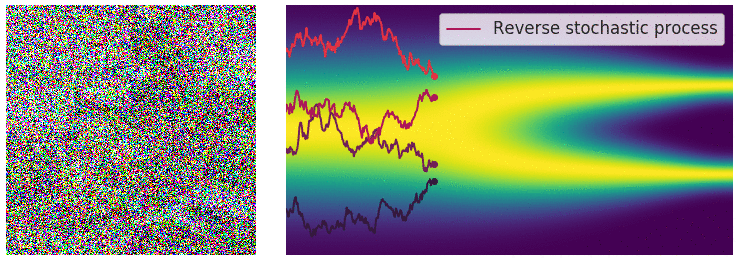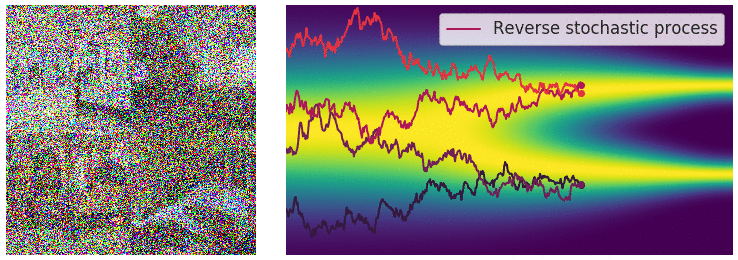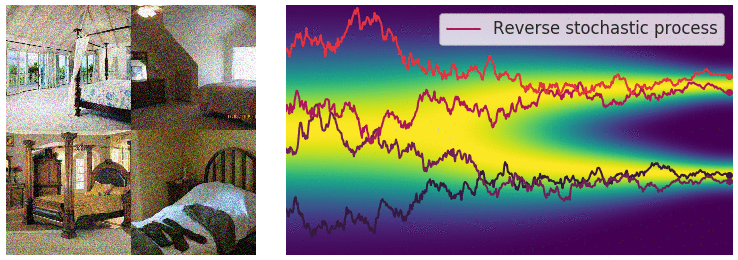
샘플링 과정은 Fig 12에서 보는 바와 같이, diffusion 모델의 reverse process와 같다. SDE도 time step
학습된 score-based model
Score-based model
Forward SDE, reverse SDE 전체 과정은 다음과 같이 그림으로 나타낼 수 있다.
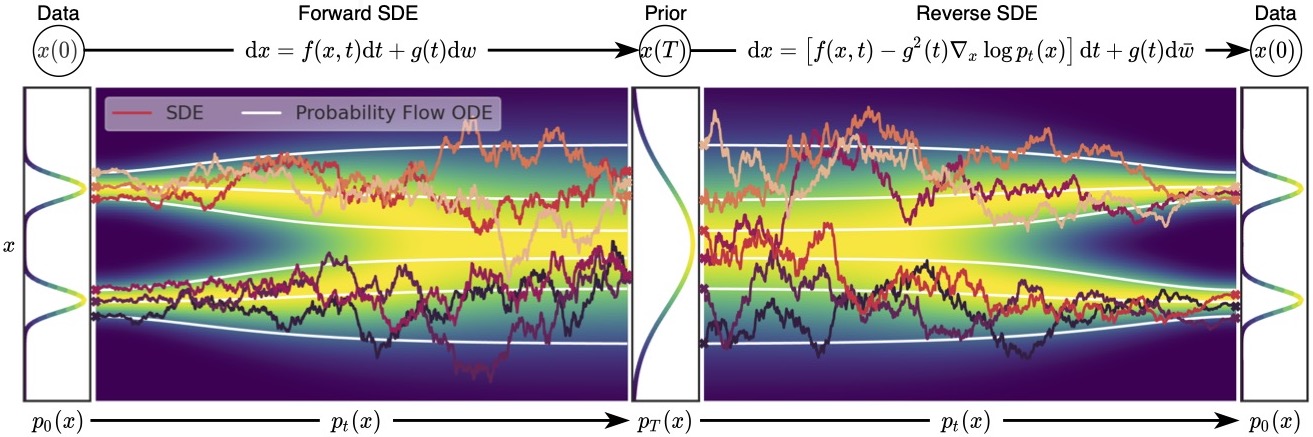
Fig 13에서 흰색 선은 ODE(ordinary differential equation, 상미분방정식 )를 활용해서, 즉 forward process와 reverse process를 deterministic하게 모델링한 경우이다. Continuous한 normalizing flow로 해석해볼 수 있는데, 여기서는 자세히 다루지 않겠다. 더 자세한 내용은 링크를 참조하자.








최근댓글