목차
앞서 대표적인 심층 생성 모델인 AutoRegressive Models (ARMs), Flow-based Models 두 가지를 살펴보았다. 하지만, (적어도 내가 연구하고 있는 분야에서는) 최근에는 VAE, Diffusion, GAN 기반의 모델이 활발하게 이용된다. 특히 diffusion의 우수한 성능은 따로 설명이 필요 없을 정도로 유명하고(실제로 세계적인 학회에 가면 과장 조금 보태서 30~40% 정도는 diffusion 관련 논문이 쏟아지고 있다.), VAE와 GAN을 기반으로 하는 다양한 우수한 성능을 보이는 모델이 나오고 있다.
VAE는 latent variable을 다룰 수 있다는 점에서 최근에는 생성모델 자체로 쓰이기 보다는 다양한 아키텍쳐들의 기반(base)으로 많이 사용되고 있다. 또한, diffusion은 다양한 관점에서 설명이 가능한데, VAE에서 활용되는 이론이 diffusion에서도 활용되며, 아예 diffusion을 hierarchical VAE로 보기도 한다. 따라서 책 'Deep Generative Modeling'을 참고하여 VAE에 대해 자세하게 공부하고, 정리해보려 한다.
Autoregressive Models(ARMs), Flow-based Models, and Latent Variable Models
먼저, 앞에서도 계속 살펴봤던 deep generative models의 분류 그림과 비교 표를 한 번 살펴보고 넘어가자.


ARMs and Flow-based Models
ARM과 flow-based model은 Likelihood를 직접적으로 모델링(cf. implicit → GAN, approximation → VAE)하므로, 학습(train)과 평가(eval)가 쉽고 안정적이라는 특징이 있다.
ARM은 Chain rule을 기반으로
하지만 sequential하게 생성할 수밖에 없고, unsupervised 방식으로 feature를 학습하지 못한다.
Flow-based model은 invertible transformation function을 사용하여 간단한 distribution을 복잡한 distribution으로 변형하는 방식으로 생성한다. Change of variables 식을 사용하여 marginal likelihood를 얻을 수 있으며, 일종의 directed latent variable model로 볼 수 있다.
하지만 triangular Jacobian 계산이 가능해야 하며, log-likelihood의 평가(eval)가 효율적이어야 한다.
Latent Variable Models
이미지의 생성 과정을 예로 들어보자. 어떤 이미지 데이터가 있을 때 새로운 이미지를 생성하는
어떤 물체를 사람에게 그리라고 지시하면, 실루엣을 먼저 그린 후 크기나 형상을 그리고, 그 다음에 디테일을 추가하고, 마지막으로 배경을 그릴 것이다. 이처럼 인공지능 모델이 다룰 데이터에도 실루엣, 크기, 디테일, 배경 등의 factor가 존재할 것이다.
Generative process

활용할 용어(변수)를 살펴보자.
생성이 이루어지는 과정은 다음과 같다.
- Latent variable
- Latent variable
확률 개념(probability distribution)을 사용하기 때문에 완벽하게 같은 이미지를 생성하는 것은 거의 불가능하며, 이는 생성모델의 diversity 특성과 연관이 있다.
Latent Variable Models
Latent variable
모델을 학습할 때에는 data
좀 더 구체적으로 살펴보자.
목표는 주어진 data(observations)

Latent variable model에서는 Fig 4와 같이 latent variable
위 식을 Fig 4의 오른쪽 그림처럼
Probabilistic Principal Component Analysis (pPCA)
probabilistic Principal Component Analysis (pPCA)는 latent variable model을 확률로 가장 간단하게 모델링할 수 있는 이론이다.
먼저, 모델링에 필요한 가정을 살펴보자.
- Continuous random variables
Gaussian distribution의 성질과 세 번째 가정에 따라 conditional probabiliaty
이어서, normal distribution을 따르는 두 벡터의 선형 결합 성질에 따라
이제 log-likelihood function
그리고 Gaussian 성질을 활용하여
여기서 matrix
따라서, log-likelihood function을 최대화하는 계산 가능한
하지만, pPCA를 활용한 모델링에는 치명적인 한계가 있다. 가정에서 linear dependency 대신 non-linear dependency를 가지거나, Gaussian 외의 다른 distribution을 사용하면 integral을 계산할 수 없다. 따라서 좀 더 일반적인 상황에서는 log-likelihood에 대한 근사(approximation)가 필요하다.
Variational Auto-Encoders (VAEs)
다음으로, VAE를 이해하는 데 필요한 핵심 내용인 variational inference와 ELBO 유도 과정을 살펴보자. VAE는 nonlinear latent variable model을 모델링하기 위해 variational inference 개념을 활용한다.
먼저 Monte Carlo approximation을 알아보자. MC approximation은 계산이 불가능한 기댓값 계산을 근사하는 가장 간단한 방법이다.
Latent prior
기존
Variational inference and ELBO
먼저 용어를 정의하자.
Marginal distribution에 log를 취하여 log likelihood
Jensen’s inequality에 따라 기댓값과 log 자리가 바뀌면 부등호가 생긴다.
여기서
Amortization이란 우리말로 분할 상환이라는 뜻을 갖는다. 모델 학습 시 주어진 input에 대한 distribution의 parameter를 반환하는데, stochastic한 방법으로(batch에 따라 나누어서) 진행한다고 해석해볼 수 있다.
이에 따라 VAE는 Stochastic encoder
Log-likelihood의 lower bound는 Evidence Lower BOund (ELBO)로 표현하며, 다음과 같이 구성된다.
- VAE를 학습한다. → ELBO를 maximize한다. → VAE decoder가 latent variable
- VAE를 학습한다. → ELBO를 maximize한다. → VAE decoder가 latent variable
- VAE를 학습한다. → ELBO를 maximize한다. → VAE encoder의 output distribution이 prior(보통 standard Gaussian)와 가까워 지도록 한다. (너무 간단해지면 오히려 posterior collapse 문제를 야기한다. Posterior collapse는 다음 글에서 간단히 다뤄볼 것이다.)
Different Perspective on the ELBO
마지막 KL divergence term은 항상 0보다 크거나 같으므로, 위에서 유도한 ELBO와 동일한 term을 얻을 수 있다.
유도 과정을 통해 VAE의 문제점을 알아볼 수 있다.
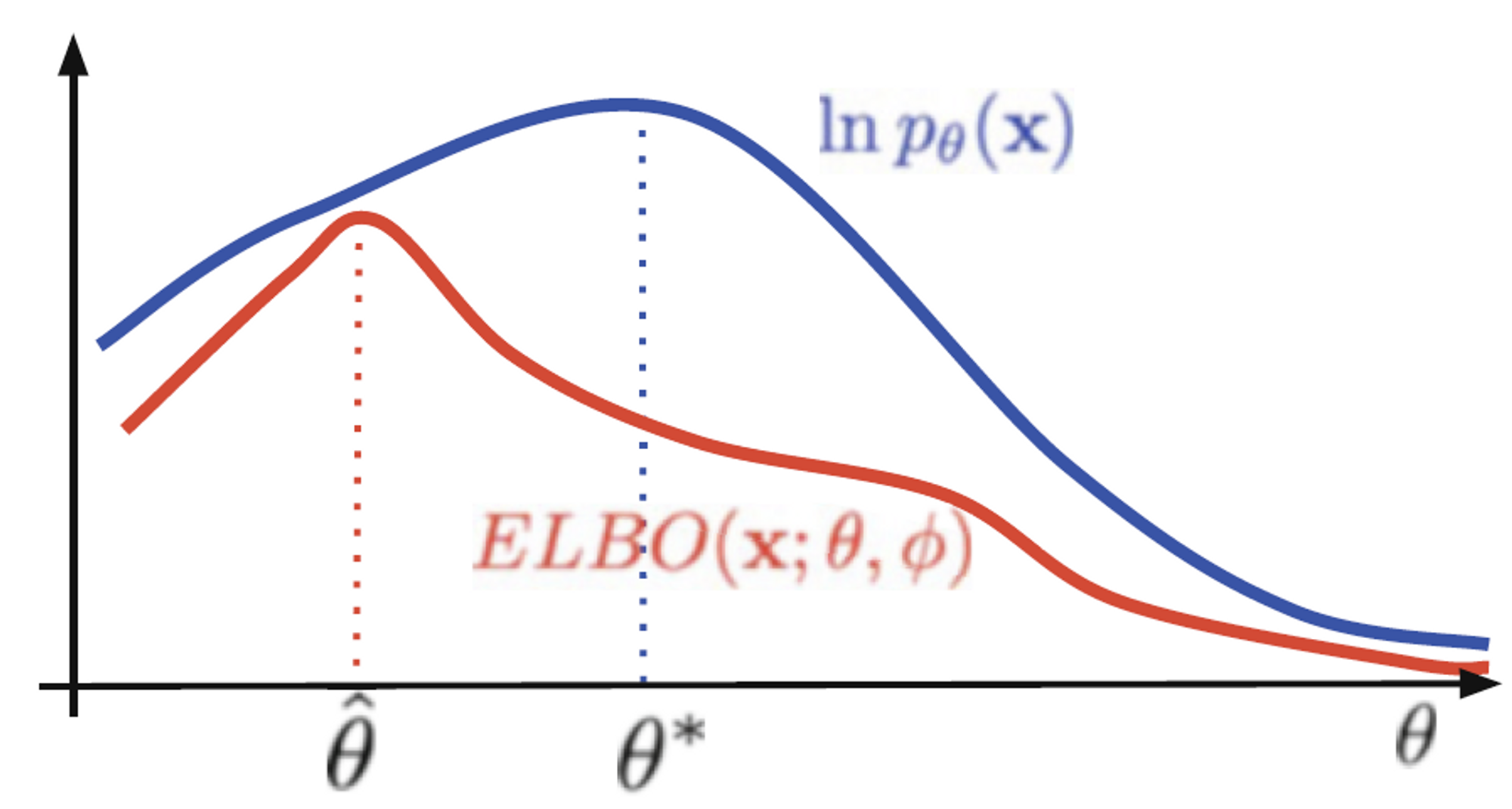
실제 posterior를 알 수 없지만, KL divergence의 성질에 따라 항상 0보다 크거나 같으므로 해당 값을 무시하는데, 값이 너무 커진다면 (즉 variational posterior








최근댓글