Graph Neural Networks (3) - Implementation, Stacking Layers, Graph Manipulation

연구를 하면서 머신러닝에 사용되는 Graph에 관해 알아둘 필요가 있어, 관련 기초 내용을 알차게 다루는 Stanford CS224W 강의를 수강하고, 내용을 정리하려 한다.

 

유튜브 강의 링크는 다음과 같다.

 

https://www.youtube.com/playlist?list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn 

Stanford CS224W: Machine Learning with Graphs

 

 

목차

 

 

이제까지 single GNN layer가 어떻게 동작하는지와 GCN, GraphSAGE, GAT 모델에 대해 자세히 알아보았다.

https://jjuke-brain.tistory.com/entry/Graph-Neural-Networks-1-Deep-Learning-for-Graphs-GCN-GraphSAGE

Graph Neural Networks (1) - Deep Learning for Graphs, Message and Aggregation

 

https://jjuke-brain.tistory.com/entry/Graph-Neural-Networks-2-GNN-Framework

Graph Neural Networks (2) - GNN Framework, GraphSAGE, GAT

 

 

전체 GNN의 동작 과정을 다시 한 번 살펴보자.

 

General GNN Framework

 

여기서 (1), (2)까지 이전 글에서 상세하게 다루었다.

이번에는 (3), (4) 과정을 알아볼 것이다.

 

 

 

 

Implementation of Single GNN Layer

 

먼저, 이전 글에 이어 single GNN layer를 실제 구현할 때 적용하는 유용한 trick을 소개해보려 한다.

 

GNN Layer in practice

 

GNN을 구현하여 사용할 때, single GNN layer는 위와 같이 다양한 deep learning module을 포함시킬 수 있다.

• Batch normalization
  • Node embedding들을 normalize(zero mean, unit variance)하는 trainable parameter \(\boldsymbol{\gamma, \beta}\)를 사용하여 안정적인 training을 할 수 있게 해준다.
• Dropout
  • Training 중에 layer의 node를 제외시킴으로써 Overfitting을 막아준다.
  • GNN에서는 message computation 과정에 적용된다.
• Activation
  • Rectified linear unit(ReLU), Sigmoid, Parametric ReLU 등을 사용하여 nonlinearity를 부여한다.
• Attention/Gating : Message의 importance를 반영해준다.
• etc...

 

Model Design 과정에 필요한 모듈은 'GraphGym'이라는 패키지에서 제공한다.

 

 

 

 

 

 

 

Layer Connectivity

 

GNN Layer를 연결할 때에는 각 layer를 순서대로 쌓고, skip connection을 적용한다.

 

 

 

 

Stacking GNN Layers

 

GNN을 구성하는 가장 간단한 방법은 순서대로 GNN layer를 쌓는 것이다.

 

Simply Stacking GNN Layers

 

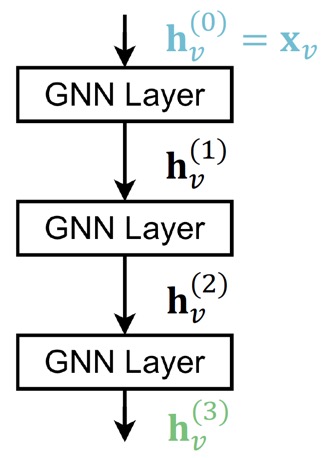
Input은 initial raw node feature \(\mathbf{x}_v\)이고, output은 \(L\)개의 GNN layer를 거친 후의 node embedding \(\mathbf{h}_v^{(L)}\)이다.

 

 

 

Over-smoothing Problem

 

하지만 이렇게 단순히 많은 layer를 쌓게 되면 over-smoothing problem이 발생한다.

Over-smoothing problem이란, 모든 node embedding이 같은 값으로 수렴되어버리는 현상을 말한다. 이렇게 되면 node embedding을 통해 서로 다른 노드를 구별하려고 하는 본래 목적을 잃게 된다.

왜 이러한 현상이 발생하는지 알기 위해서는 GNN에서의 receptive field를 이해해야 한다.

Receptive field는 관심있는 node의 embedding을 결정하는 node set을 말한다. 쉽게 말해, target node의 embedding에 영향을 주는 node의 범위의 개념이다.

K개 layer의 GNN에서 각 노드는 아래와 같이 K-hop neighborhood만큼의 receptive field를 갖는다.

 

Receptive field of K-layer GNN (for one node)

 

위와 같이 layer가 깊어질수록 receptive field가 기하급수적으로 늘어난다. ('7다리만 건너면 지구 상의 모든 사람과 친구이다.'라는 말이 떠오른다.)

 

Receptive field overlapping

 

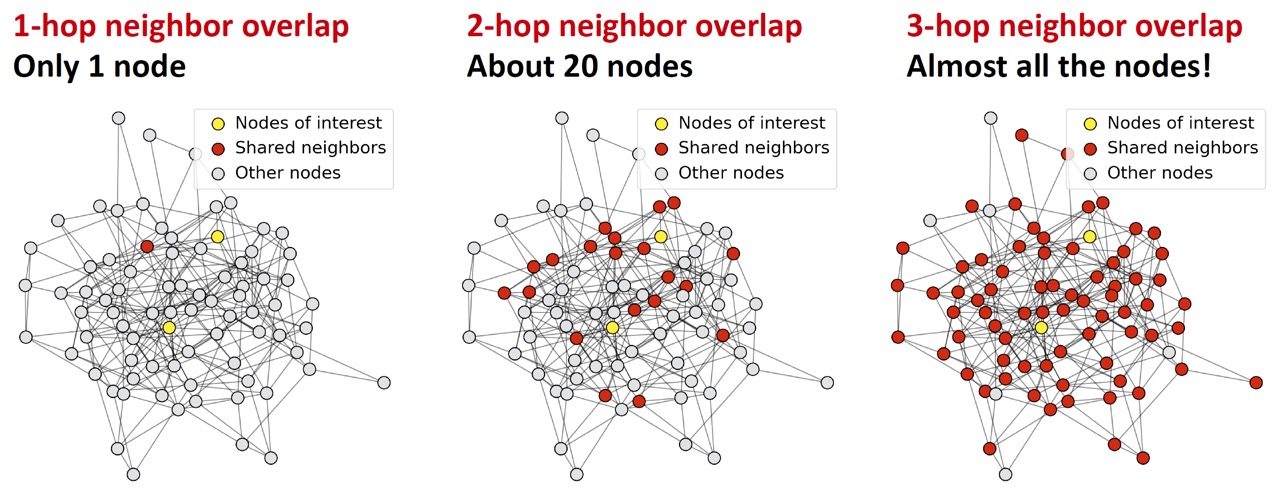
이때문에 위와 같이 layer가 깊어질수록 서로 다른 두 노드에 대한 receptive field(k-hop neighbor)가 많이 겹치게 되고, 이로 인해 모든 node embedding이 같은 값을 갖게 되는 것이다.

 

 

 

GNN Layer Connectivity

 

따라서 over-smoothing problem 때문에 이미지를 다루는 CNN 등의 domain에서와는 달리, layer를 깊게 쌓는다고 해서 성능이 좋아지지 않는다. 이를 방지하기 위해서는 GNN layer를 추가할 때 아래와 같은 요건을 확인해보아야 한다.

1. Graph의 diameter를 계산해보는 등 필요한 receptive field를 확인해본다.
2. GNN layer의 수 \(L\)을 위에서 분석한 receptive field보다 약간 더 크게 세팅한다.

 

그렇다면 GNN에서 layer가 적을 때(=shallow할 때) expressive power를 강화하려면 어떻게 해야할까?

 

 

Solution 1. 각 GNN layer 내에서의 expressive power를 증가시킨다.

이전에 transformation(message computation)과 aggregation function에 간단히 single linear layer를 사용했다.

대신 aggregation/transformation에 deep neural network(MLP 등)를 적용한다면, GNN layer 내에서의 expressive power가 증가할 것이다.

 

 

Solution 2. Message passing을 하지 않는 layer를 추가한다.

GNN에서 꼭 GNN layer만 추가되어야 하는 것은 아니다. 아래와 같이 pre-process layer와 post-process layer로 MLP layer를 추가해줄 수 있다.

 

Added MLP layers for pre-process layer and post-process layer

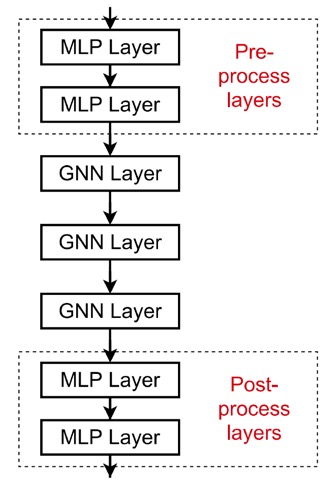
• Pre-processing layers : Node feature를 인코딩해야할 때 사용한다. 예를 들어, node가 image 또는 text를 표현하는 경우가 있다.
• Post-processing layers : Node embedding들에 대한 reasoning, transformation 등이 필요할 때 사용한다. 예를 들어, graph classification이나 knowledge graph 등에 활용된다.

 

 

 

 

Skip Connections in GNN

 

위와 같은 방법으로도 expressive power가 부족하여, layer를 더 쌓아야 할 때에는 skip connection을 활용한다.

 

Skip Connection

 

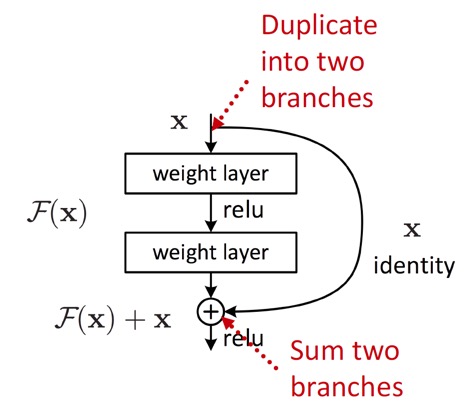
Skip connection이란, 위와 같이 layer의 input을 두 branch로 나누어 하나는 layer를 거치고, 하나는 입력 상태 그대로 더해주는 방법이다. (ResNet에서의 그 skip connection 개념이다.)

Over-smoothing problem이 발생할 때에는 이전 layer가 노드를 더 잘 구별하는데, skip connection을 통해 최종 node embedding 결과에 이전 layer의 영향을 높여줄 수 있다.

 

GNN with Skip Connection

 

예를 들어, 일반적인 GCN layer의 aggregation은 다음과 같다.

\( \mathbf{h}_v^{(l)} = \sigma \left( \sum_{u \in N(v)} \mathbf{W}^{(l)} \cfrac{\mathbf{h}_u^{(l-1)}}{\lvert N(v) \rvert} \right) \)

 

Skip connection을 적용한 GCN layer는 다음과 같이 표현할 수 있다.

\( \mathbf{h}_v^{(l)} = \sigma \left( \sum_{u \in N(v)} \mathbf{W}^{(l)} \cfrac{\mathbf{h}_u^{(l-1)}}{\lvert N(v) \rvert} + \mathbf{h}_v^{(l-1)} \right) \)

• \(\mathcal{F}(\mathbf{x})\) \(\Rightarrow\) \( \sum_{u \in N(v)} \mathbf{W}^{(l)} \cfrac{\mathbf{h}_u^{(l-1)}}{\lvert N(v) \rvert} \)
• \( \mathbf{x} \) \(\Rightarrow\) \( \mathbf{h}_v^{(l-1)} \)

 

Skip connection을 다음과 같이 적용할 수도 있다.

 

Directly skip to the last layer

 

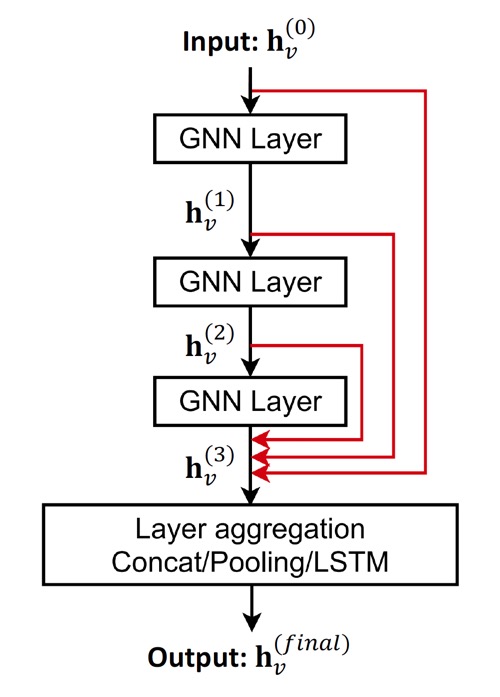
처음 layer의 input부터 모든 layer의 input을 마지막 layer 결과와 더해주어서 모든 이전 layer의 node embedding들을 종합하는 것이다.

 

 

 

 

 

Graph Manipulation in GNNs

 

다음으로, GNN framework의 4번째 과정인 graph manipulation을 살펴보자.

 

General GNN Framework

 

실제로 input graph와 computation graph는 다르다. GNN 과정에서 graph에 feature augmentation이나 structure augmentation을 적용해주기 때문이다.

 

이전까지는 raw input graph와 computational graph가 같다고 가정했으나, 이 경우 다음과 같은 문제가 발생한다.

• Feature level
  • Input graph의 feature가 부족한 경우
    • Feature augmentation으로 해결한다.
• Structure level
  • Input graph가 너무 sparse한 경우 → Message passing 과정 자체가 비효율적이다.
    • Virtual node/edge를 추가하여 해결한다.
  • Input graph가 너무 dense한 경우 → Message passing의 비용(cost)이 너무 많이 든다.
    • Message passing 시 이웃 노드를 샘플링하여 해결한다.
  • Input graph의 size가 너무 큰 경우 → GPU에 computational graph를 맞출 수 없다.
    • Embedding 계산 시 subgraph를 샘플링하여 해결한다.

 

각 경우에 대한 해결 방법을 좀 더 자세히 알아보자.

 

 

 

 

Feature Augmentation

 

실제로 input graph가 node feature를 가지지 않는 경우, 즉 adjacency matrix만 갖고 있는 경우가 많다.

이때 node에 상수 값을 할당하거나, node의 id(index)에 따른 one-hot vector를 할당하여 GNN을 적용한다.

두 방법의 특징을 표로 비교해보자.

	Constant node feature	One-hot node feature
Expressive Power	보통 - 모든 노드가 동일한 값을 갖는다.	높음 - 각 노드는 유일한 id를 가지므로 각 노드의 특정한 정보를 담을 수 있다.
Inductive Learning (Generalize to unseen nodes)	높음 - 새로운 노드에 간단히 적용할 수 있다. (간단히 상수를 할당해주어서 GNN을 적용하면 된다.)	낮음 - 새로운 노드는 새로운 id를 갖기 때문에 GNN이 본 적 없는 id를 임베딩할 수 없다.
Computational Cost	낮음 - 1차원 feature	높음 - O(|V|) 차원의 feature large graph에 적용 불가
Use Cases	Inductive setting을 갖는 graph	size가 작고, transductive setting을 갖는 graph

 

그리고, 그래프의 구조 중에 GNN이 학습하기 어려운 구조도 있다.

예를 들어, GNN은 cycle의 길이를 알 수 없다.

 

GNN can't recognize cycles

 

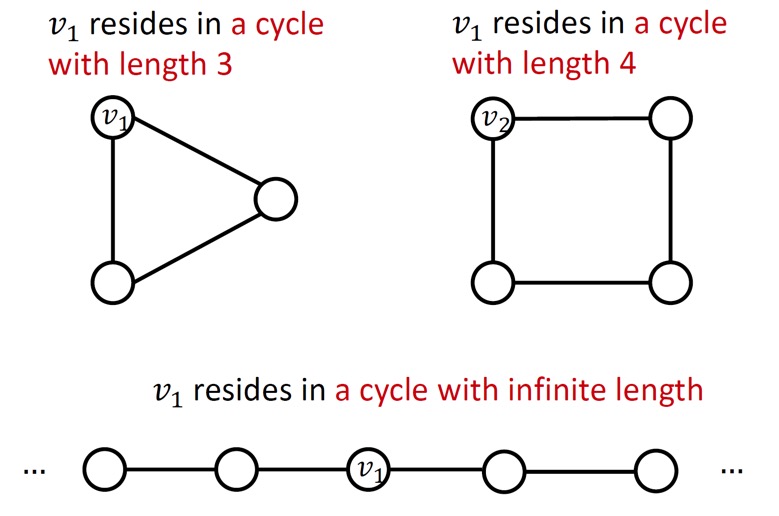
위 그림에서의 노드 \(v\)는 분명 세 경우 다 다른 graph 구조를 갖지만, 모두 degree가 2이기 때문에 computation graph는 다음과 같은 binary tree 구조로 이루어지게 된다.

 

All input graphs have same computation graphs

 

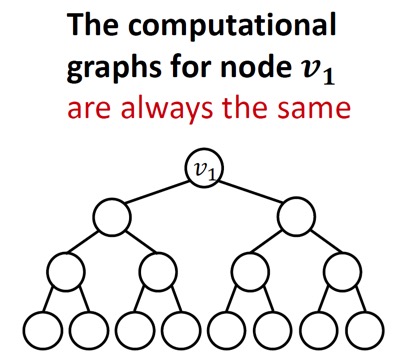
이를 해결하는 방법은 cycle을 세는 feature를 node feature에 추가해주는(augment)것이다.

예시에서 \(v_1\)의 node feature에는 cycle length가 3인 augmented node feature \(\left[ 0, 0, 0, 1, 0, 0 \right]\)를, \(v_2\)의 node feature에는 cycle length가 4인 augmented node feature \(\left[ 0, 0, 0, 0, 1, 0 \right]\)를 할당해준다.

 

이외에도 augmented feature로 Clustering coefficient, PageRank, Centrality 등 다양한 feature를 활용할 수 있다. (앞서 graph feature representation에서 알아봤던 어떤 feature든 사용 가능하다.)

 

 

 

 

Adding Virtual Nodes/Edges

 

Input graph가 너무 sparse한 경우에는 가상의 엣지나 노드를 추가한다.

 

 

Add virtual edges

가상의 edge를 만들어 2-hop neighbor까지 연결시킨다. 이는 간단히 GNN 계산에 adjacency matrix \(\mathbf{A}\) 대신 \(\mathbf{A} + \mathbf{A}^2\)를 사용하는 것이다.

주로 bipartite graph에서 많이 사용한다.

예를 들어, author-to-papers 관계를 갖는 bipartite graph가 있다고 하면, 2-hop virtual edge를 통해 저자 간의 collaboration graph를 생성할 수 있다.

 

 

Add virtual nodes

Virtual node는 그래프의 모든 노드에 연결되는 가상의 노드이다.

 

Adding virtual node

 

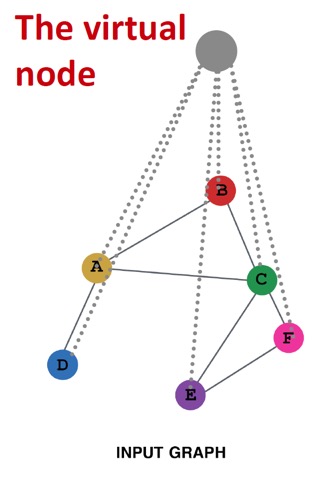
Sparse한 graph(즉, edge가 많이 없는 graph)에서는 두 노드간의 최단경로가 비효율적으로 큰 경우가 있는데, virtual node를 추가하면 모든 노드간의 최단 경로가 2가 된다.

이를 통해 message passing의 효율성을 향상시킨다.

 

 

 

 

Node Neighborhood Sampling

 

이제까지는 모든 이웃노드를 message passing에 사용했다.

하지만, input graph가 dense한 경우에는 message passing의 계산 과정이 오래 걸릴 수 있다.

이를 해결하기 위해 message passing을 적용할 때마다 이웃 노드를 랜덤으로 샘플링한다.

이를 여러 번 반복하는 경우, 모든 이웃 노드를 사용할 때와 비슷한 embedding을 얻을 수 있고, 동시에 computational cost는 낮춰 효율적으로 학습을 진행할 수 있다. (실제로도 잘 동작한다고 한다.)