연구를 하면서 머신러닝에 사용되는 Graph에 관해 알아둘 필요가 있어, 관련 기초 내용을 알차게 다루는 Stanford CS224W 강의를 수강하고, 내용을 정리하려 한다.
유튜브 강의 링크는 다음과 같다.
https://www.youtube.com/playlist?list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn
Stanford CS224W: Machine Learning with Graphs
This course covers important research on the structure and analysis of such large social and information networks and on models and algorithms that abstract ...
www.youtube.com
목차
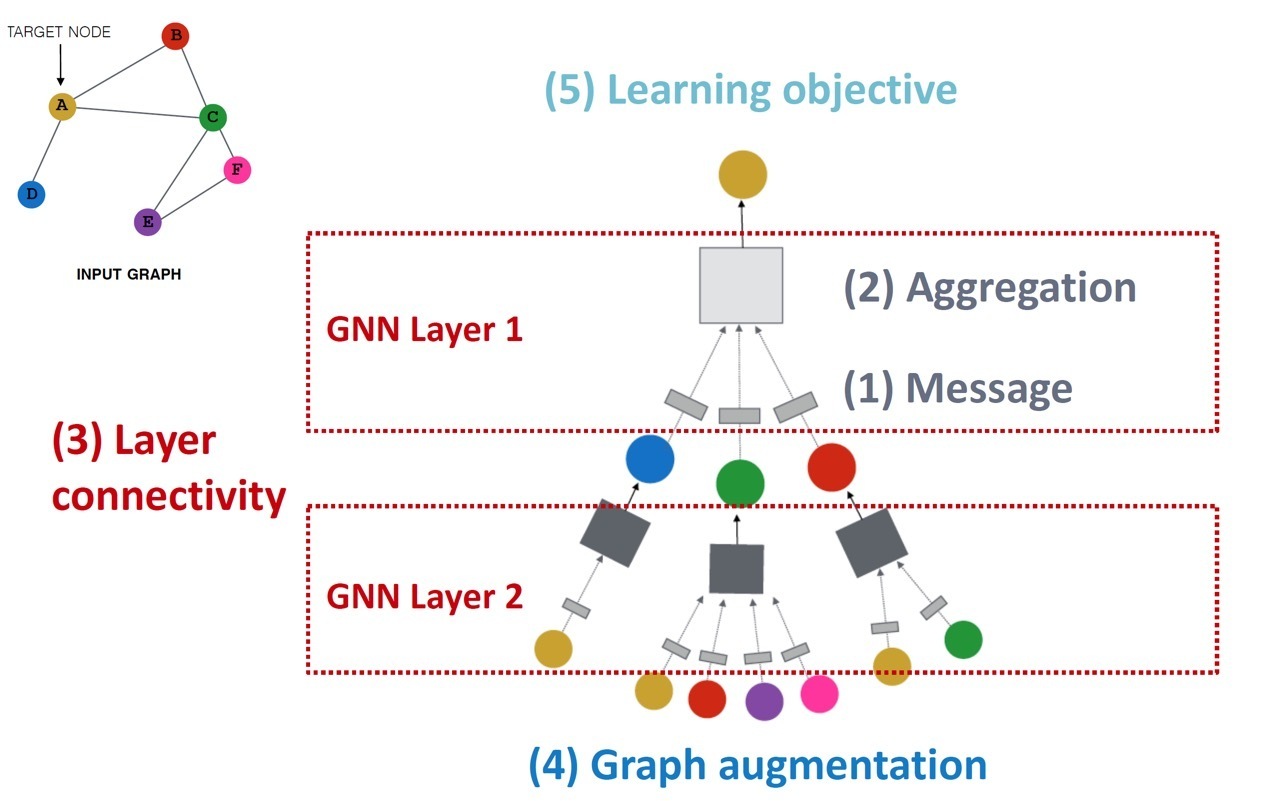
3개의 글에 걸쳐 GNN의 일반적인 동작 과정을 따라 (1) Message computation, (2) Aggregation, (3) Layer connection, (4) Graph augmentation(manipulation) 까지 알아보았다.
https://jjuke-brain.tistory.com/entry/Graph-Neural-Networks-1-Deep-Learning-for-Graphs-GCN-GraphSAGE
Graph Neural Networks (1) - Deep Learning for Graphs, Message and Aggregation
연구를 하면서 머신러닝에 사용되는 Graph에 관해 알아둘 필요가 있어, 관련 기초 내용을 알차게 다루는 Stanford CS224W 강의를 수강하고, 내용을 정리하려 한다. 유튜브 강의 링크는 다음과 같다. htt
jjuke-brain.tistory.com
https://jjuke-brain.tistory.com/entry/Graph-Neural-Networks-2-GNN-Framework
Graph Neural Networks (2) - GNN Framework, GraphSAGE, GAT
연구를 하면서 머신러닝에 사용되는 Graph에 관해 알아둘 필요가 있어, 관련 기초 내용을 알차게 다루는 Stanford CS224W 강의를 수강하고, 내용을 정리하려 한다. 유튜브 강의 링크는 다음과 같다. htt
jjuke-brain.tistory.com
Graph Neural Networks (3) - Implementation, Stacking Layers, Graph Manipulation
연구를 하면서 머신러닝에 사용되는 Graph에 관해 알아둘 필요가 있어, 관련 기초 내용을 알차게 다루는 Stanford CS224W 강의를 수강하고, 내용을 정리하려 한다. 유튜브 강의 링크는 다음과 같다. htt
jjuke-brain.tistory.com
이 글에서는 마지막으로 GNN을 training하는 과정, (5) Learning objective 부분을 알아볼 것이다.
Training은 어떻게 진행하며, output은 어떻게 다루고, loss fuction은 무엇인지 등을 자세하게 알아보자.
Training GNN - Prediction
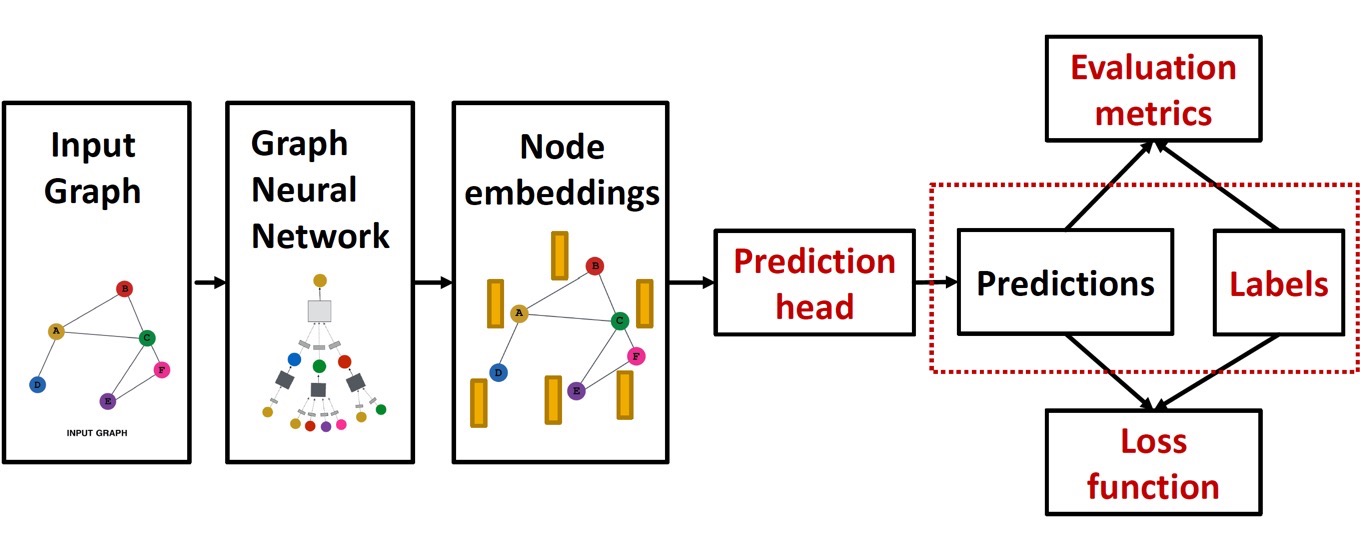
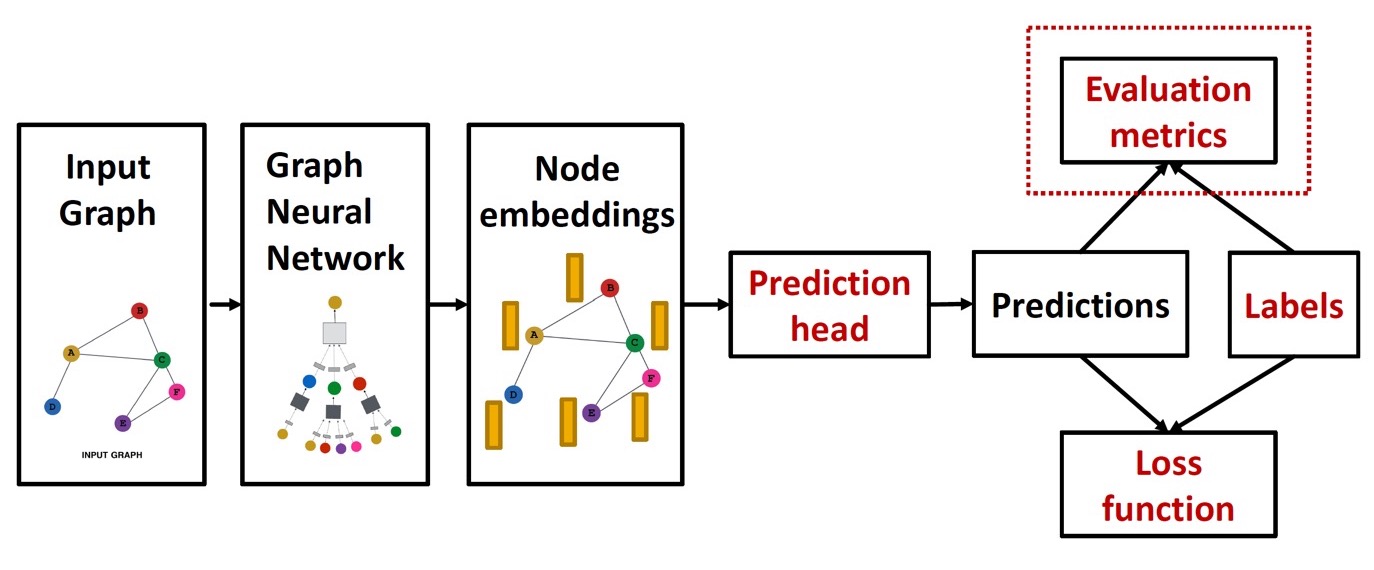
GNN을 training하는 pipeline은 다음과 같다.
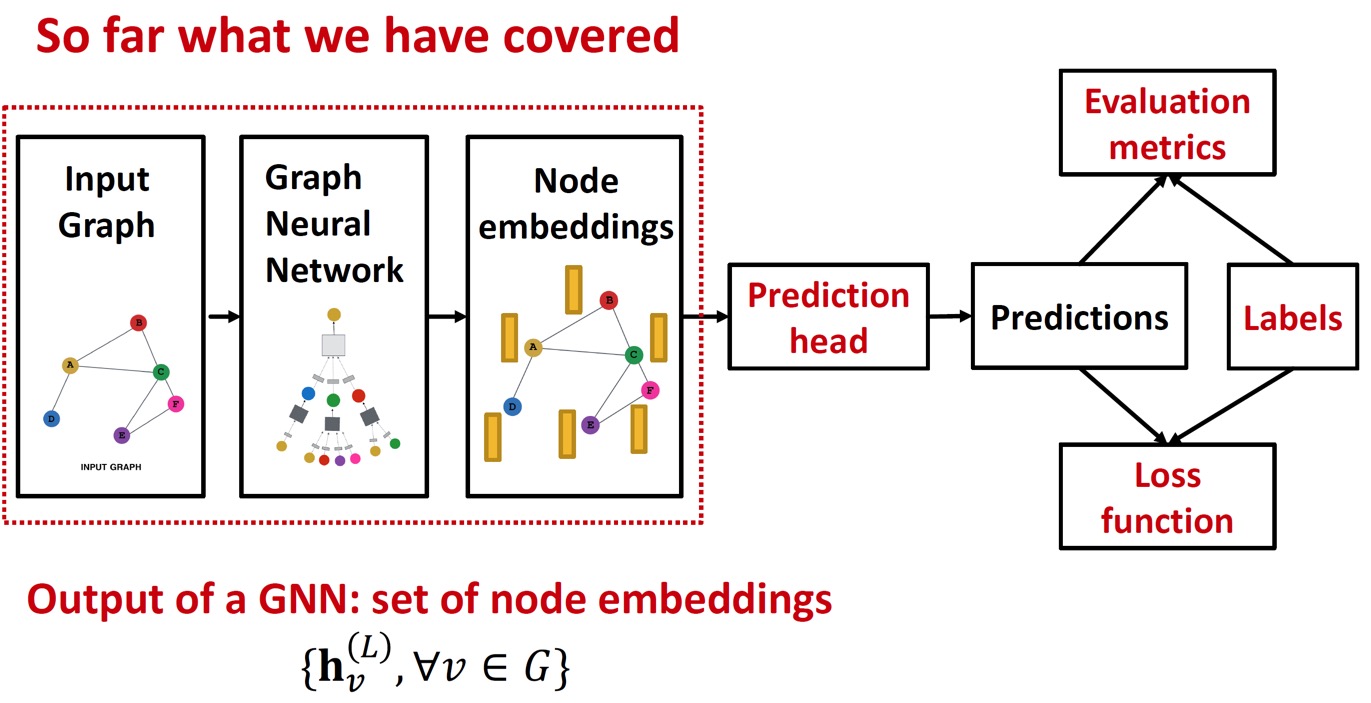
이제까지 node embedding 과정을 배웠고, 이제 GNN의 output으로 prediction을 어떻게 진행하는지(예측값을 어떻게 구할 것인지) 알아보자.
Prediction head는 task에 따라 다음과 같이 나뉜다.
- Node-level tasks → node-level prediction 필요
- Edge-level tasks → edge-level prediction 필요
- Graph-level tasks → graph-level prediction 필요
Node-level Prediction
Node-level prediction은 GNN의 output인 node embedding을 직접적으로 사용한다.
GNN 결과 \(d\)차원의 node embedding \(\left\{\mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G\right\}\) 을 얻는다.
k-way prediction을 한다고 가정하자. k-way prediction이란, k개 카테고리 중에서 분류(classify)하거나 k개 target에 대해 regression하는 것을 말한다.
이때, 예측값은 다음과 같이 표현할 수 있다.
\( \hat{\mathbf{y}}_v = \text{Head}_{\text{node}} \left( \mathbf{h}_v^{(L)} \right) = \mathbf{W}^{(H)} \mathbf{h}_v^{(L)} \)
- \(\mathbf{W}^{(H)} \in \mathbb{R}^{k \times d}\) : Node embedding \(\mathbf{h}_v^{(L)} \in \mathbb{R}^d\)을 예측값 \(\hat{\mathbf{y}}_v \in \mathbb{R}^k\)으로 mapping하는 weight matrix이다. 이를 통해 loss를 계산한다.
Edge-level Prediction
Edge-level prediction은 node embedding 쌍을 이용한다.
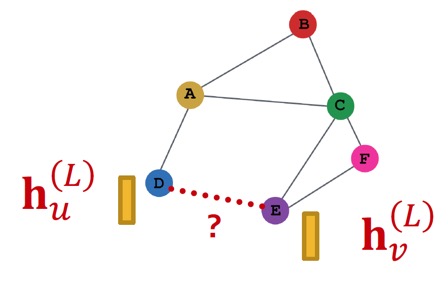
Edge-level에서의 prediction은 두 노드간에 연결이 되었는지 아닌지를 예측하는 것이다.
K-way prediction을 한다고 가정할 때, 예측값은 다음과 같다.
\( \hat{\mathbf{y}}_{uv} = \text{Head}_{\text{edge}} \left( \mathbf{h}_u^{(L)}, \mathbf{h}_v^{(L)} \right) \)
수식에서 \(\text{Head}_{\text{edge}}\)에 사용할 수 있는 함수는 다음과 같다.
(1) Concatenation + Linear
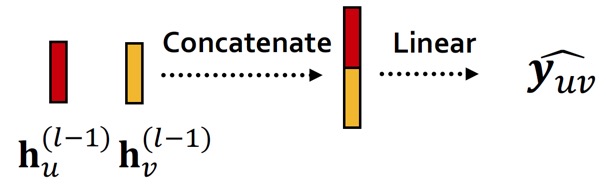
Graph attention에서 소개한 방법으로, 두 embedding을 연결한 후에 single linear layer를 거치는 방법이다.
\( \hat{\mathbf{y}}_{uv} = \text{Linear}\left( \text{Concat} \left(\mathbf{h}_u^{(L)}, \mathbf{h}_v^{(L)} \right) \right) \)
여기서 \(\text{Linear}\)함수는 연결된(concatenated) 2-dimensional embedding을 \(k\)-dimensional embedding(k-way prediction)로 맵핑한다.
(2) Dot Product
일반적인 dot product는 아래와 같다.
\( \hat{y}_{uv} = \left( \mathbf{h}_u^{(L)} \right)^\top \mathbf{h}_v^{(L)} \)
하지만 이 경우, 1-way prediction만 가능하다. 결과값이 scalar, 즉 1차원 embedding이기 때문이다.
Edge-level prediction에서 1-way prediction은 두 노드 사이에 edge가 존재하는지 아닌지를 판단하는 경우에만 활용이 가능하다.
이를 k-way prediction으로 확장하기 위해서는 아래와 같이 multi-head attention과 비슷한 방법으로 진행한다.
\( \hat{\mathbf{y}}_{uv}^{(1)} = \left( \mathbf{h}_u^{(L)} \right)^\top \mathbf{W}^{(1)} \mathbf{h}_v^{(L)} \)
\( \cdots \)
\( \hat{\mathbf{y}}_{uv}^{(k)} = \left( \mathbf{h}_u^{(L)} \right)^\top \mathbf{W}^{(k)} \mathbf{h}_v^{(L)} \)
\( \hat{\mathbf{y}}_{uv} = \text{Concat} \left( \hat{\mathbf{y}}_{uv}^{(1)}, \dots, \hat{\mathbf{y}}_{uv}^{(k)} \right) \in \mathbb{R}^k \)
Class마다 trainable weight \(\mathbf{W}\)가 존재하고, product 결과에 이를 반영하여 최종적으로 연결해주는 것이다.
Graph-level prediction
Graph-level prediction은 그래프 내의 모든 노드의 embedding을 활용하여 prediction을 진행하는 것이다.
k-way predicgtion을 진행한다고 했을 때, graph-level prediction은 아래 수식을 통해 이루어진다.
\( \hat{\mathbf{y}_G} = \text{Head}_{\text{graph}} \left( \left\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \right\} \right) \)
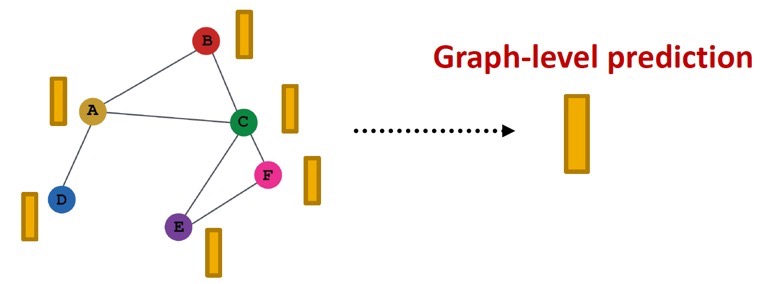
\(\text{Head}_{\text{graph}} (\cdot)\)는 노드 전체의 정보를 하나로 나타내는 개념이기 때문에 GNN layer의 \(\text{AGG} (\cdot)\)과 비슷하다.
\(\text{Head}_{\text{graph}}\)에는 다음과 같은 함수를 사용할 수 있다.
(1) Global mean pooling
\( \hat{\mathbf{y}}_G \text{Mean} \left( \left\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \right\} \right) \)
(2) Global max pooling
\( \hat{\mathbf{y}}_G \text{Max} \left( \left\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \right\} \right) \)
(3) Global sum pooling
\( \hat{\mathbf{y}}_G \text{Sum} \left( \left\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \right\} \right) \)
이 함수들은 작은 graph에서는 잘 동작하지만, 큰 graph에서는 잘 동작하지 못한다. Global pooling은 큰 graph의 경우, 정보를 잃기 때문이다.
예를 들어, 다음과 같은 1차원 node embedding이 있다고 하자.
\(G_1 : \left\{ -1, -2, 0, 1, 2 \right\}, \quad \quad G_2 : \left\{ -10, -20, 0, 10, 20 \right\}\)
분명히 두 그래프는 다른 node embedding들을 갖는다. (즉, structure가 서로 확실히 다르다.)
하지만, sum pooling을 진행하게 되면, \(G_1\)과 \(G_2\)에 대한 prediction 값이 똑같다.
\( G_1 : \hat{\mathbf{y}}_G = \text{Sum} \left( \left\{ -1, -2, 0, 1, 2 \right\} \right) = 0 \)
\( G_2 : \hat{\mathbf{y}}_G = \text{Sum} \left( \left\{ -10, -20, 0, 10, 20 \right\} \right) = 0 \)
즉, 이 경우 global sum pooling으로는 (그리고 mean pooling으로도) \(G_1\)과 \(G_2\)를 구별할 수 없다.
(4) Hierarchical Global Pooling
이를 해결하기 위해 Hierarchical Global Pooling을 사용한다. Hierarchical global pooling에서는 모든 node embedding들을 hierarchical하게 합친다.(aggregation)
예를 들어, non linear function \(\text{ReLU} \left( \text{Sum} (\cdot) \right) \)를 활용한 aggregation 과정을 살펴보자. 5개 노드 중에서 처음 2개 먼저 aggregate한 후, 나머지 3개를 aggregate하고, 최종 prediction을 위해 마지막으로 aggregate할 것이다.
\( G_1 : \left\{ -1, -2, 0, 1, 2 \right\} \)
\( \hat{\mathbf{y}}_a = \text{ReLU} \left( \text{Sum} \left( \left\{ -1, -2 \right\} \right) \right) = 0, \)
\( \hat{\mathbf{y}}_b = \text{ReLU} \left( \text{Sum} \left( \left\{ 0, 1, 2 \right\} \right) \right) = 3 \)
\( \therefore \hat{\mathbf{y}}_G = \text{ReLU} \left( \text{Sum} \left( \left\{ \hat{\mathbf{y}}_a , \hat{\mathbf{y}}_b \right\} \right) \right) = 3 \)
\( G_2 : \left\{ -10, -20, 0, 10, 20 \right\} \)
\( \hat{\mathbf{y}}_a = \text{ReLU} \left( \text{Sum} \left( \left\{ -10, -20 \right\} \right) \right) = 0, \)
\( \hat{\mathbf{y}}_b = \text{ReLU} \left( \text{Sum} \left( \left\{ 0, 10, 20 \right\} \right) \right) = 30 \)
\( \therefore \hat{\mathbf{y}}_G = \text{ReLU} \left( \text{Sum} \left( \left\{ \hat{\mathbf{y}}_a , \hat{\mathbf{y}}_b \right\} \right) \right) = 30 \)
이제는 \(G_1\)과 \(G_2\)를 구분할 수 있게 된다!
실제로는 이러한 hierarchically pooling 방법을 아래와 같은 방법으로 사용한다.
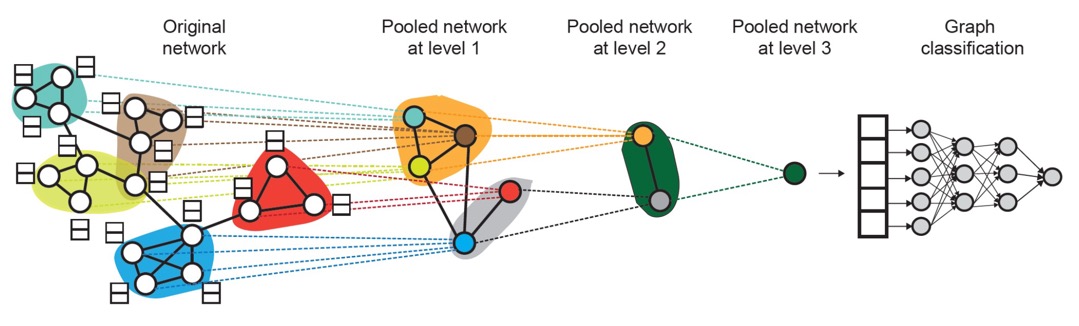
Graph에는 node들의 cluster(community) sturcture가 존재한다. 따라서 2 종류의 독립적인 GNN을 계층적으로(level에 따라) 사용한다.
- GNN A : Node embedding 계산
- GNN B : Node가 속한 cluster 계산
두 GNN은 각 level에서 병렬적으로 적용될 수있다.
각 pooling layer에서 GNN A를 통해 생성한 node embedding들을 합쳐(aggregate) GNN B를 통해 배정한 cluster를 사용한다. 각 cluster에는 새로운 노드 하나를 생성하고, 다음 pooled network를 생성하기 위해 cluster 간의 edge는 그대로 유지한다.
또한, GNN A와 GNN B는 jointly training이 가능하다.
Training GNN - GT(Ground Truth)
위에서 예측값을 구하는 과정을 알아보았다. 이제 정답값을 알면 Loss function을 구할 수 있고, 이를 optimize하여 학습을 진행할 수 있다.
GT(정답값)는 supervised labels 혹은 unsupervised signals로 구분된다.
Supervised vs Unsupervised(Self-supervised)
Graph에서 supervised learning은 label이 외부로부터 주어지는 경우이고, unsupervised learning은 graph 자체에서 얻는 signal을 활용하는 경우이다.
하지만, 둘의 차이가 불명확한 경우가 종종 있다. 즉 supervision을 활용하는 unsupervised learning이 있다.
따라서, unsupervised라는 용어보다는 self-supervised라는 용어를 많이 사용한다.
Supervised label은 node의 label \(\mathbf{y}_v\), edge의 label \(\mathbf{y}_{uv}\), graph의 label \(\mathbf{y}_G\)를 말한다. 앞서 언급했던 node의 cluster도 node의 label의 일종으로 볼 수 있다.
각각의 예시는 다음과 같다.
- Node labels \(\mathbf{y}_v\) : citation network에서, paper(node)가 속한 subject area
- Edge laebls \(\mathbf{y}_{uv}\) : transaction network에서, 거래(edge)가 사기인지 아닌지
- Graph labels \(\mathbf{y}_G\) : 여러 분자 graph들 중에서, 약과 비슷한 graphs
하지만 graph에서 얻는 unsupervised signal은 좀 복잡하다. 외부에서 주어진 값이 아니므로, self-supervised learning을 통해 graph가 내포하는 supervision signal을 찾아야 한다.
예를 들어,
- Node-level \(\mathbf{y}_v\) : clustering coefficient, PageRank 등의 Node statistics
- Edge-level \(\mathbf{y}_{uv}\) : Edge가 존재하는지 예측하는 등의 Link prediction
- Graph-level \(\mathbf{y}_G\) : 두 graph가 isomorphic한지 예측하는 등의 Graph statistics
위와 같은 값들을 예측하는 데에는 label이 따로 필요가 없다.
Training GNN - Loss Function
이제 예측값(prediction)과 정답값(label)을 구했으면, loss function을 수립하는 과정을 알아보자.
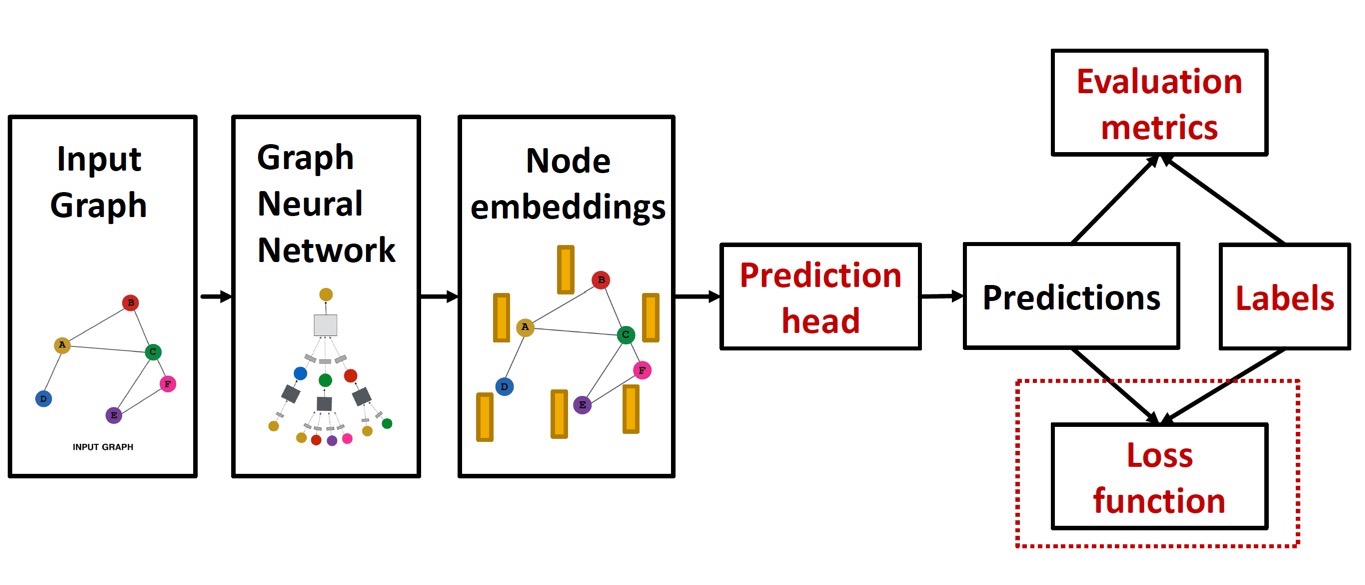
Loss를 계산하기 위해서는 크게 두 가지 방법이 있다.
- Classification Loss
- Regression Loss
우선, \(N\)개의 data point를 갖고 있다고 하자. 각 data point는 node, edge, graph가 될 수 있다. 세 가지 경우에 대한 prediction, label은 다음과 같이 표시한다.
| Prediction | Label | |
| Node-level | \(\hat{\mathbf{y}}_v^{(i)}\) | \(\mathbf{y}_v^{(i)}\) |
| Edge-level | \(\hat{\mathbf{y}}_{uv}^{(i)}\) | \(\mathbf{y}_{uv}^{(i)}\) |
| Graph-level | \(\hat{\mathbf{y}}_G^{(i)}\) | \(\mathbf{y}_G^{(i)}\) |
이때 Classification labels \(\mathbf{y}^{(i)}\)는 discrete value(category, class 등), Regresion labels \(\mathbf{y}^{(i)}\)는 continuous value(likeness 등)를 갖는다.
GNN은 두 경우 모두에 적용이 가능한데, 각각에서의 loss function과 evaluation metric이 달라진다.
Classification Loss
Classification task에서는 보통 cross entropy(CE)를 많이 사용한다.
i번째 data point에 대한 k-way prediction(k개 category 중 어디에 속하는지 예측)에서는 다음과 같은 cross entropy loss를 사용한다.
\( \text{CE} \left( \mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)} \right) = - \sum\limits_{j=1}^K \mathbf{y}_j^{(i)} \log (\hat{\mathbf{y}}_j^{(i)}) \)
- \(i\) : index of data point
- \(j\) : index of class
- \(\mathbf{y}^{(i)} \in \mathbb{R}^K\) : one-hot label encoding
- K개 요소를 갖는 벡터에서, 해당하는 index만 1, 나머지는 0
- \(\hat{\mathbf{y}}^{(i)} \in \mathbb{R}^K\) : prediction after \(\text{Softmax} (\cdot)\)
- K개 요소는 각 index에 해당할 확률을 나타냄
\(N\)개 training examples 모두에 대한 total loss는 다음과 같이 나타낸다.
\( \text{Loss} = \sum\limits_{i = 1}^N \text{CE} \left( \mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)} \right) \)
Regression Loss
Regression task에서는 보통 Mean Squared Error(MSE), 즉 L2 loss를 많이 사용한다.
i번째 data point에 대한 k-way regression은 MSE를 사용하여 다음과 같이 나타낸다.
\( \text{MSE} \left( \mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)} \right) = \sum\limits_{j=1}^K \left( \mathbf{y}_j^{(i)} - \hat{\mathbf{y}}_j^{(i)} \right)^2 \)
- \(i\) : index of data point
- \(j\) : index of target
- \(\mathbf{y}^{(i)} \in \mathbb{R}^K\) : one-hot label encoding
- K개 요소는 각 index에 해당하는 target 값(real value)을 나타냄
- \(\hat{\mathbf{y}}^{(i)} \in \mathbb{R}^K\) : prediction after \(\text{Softmax} (\cdot)\)
- K개 요소는 각 index에 해당하는 prediction 값(real value)을 나타냄
\(N\)개 training examples 모두에 대한 total loss는 다음과 같이 나타낸다.
\( \text{Loss} = \sum\limits_{i=1}^N \text{MSE} \left( \mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)} \right) \)
Training GNN - Evaluation Metrics
마지막으로, evaluation metric을 살펴보자.
Evaluation metric은 GNN이 잘 동작하는지를 측정하는 지표이다.
보통 regression에서는 accuracy, classification에서는 ROC, AUC 등이 사용된다.
Evaluation Metrics for Classification
Classification task를 평가할 때에는 보통 두 가지 경우로 나누어 평가한다.
먼저, multi-class classification의 경우에는 다음 식으로 간단히 accuracy를 계산할 수 있다. 하지만 data가 imbalance할 경우, accuracy가 높다고 무조건 좋은 것은 아니므로 주의해야 한다.
\( \cfrac{1 \left[ \text{argmax}(\hat{\mathbf{y}}^{(i)} = \mathbf{y}^{(i)} \right]}{N} \)
다음으로, class가 두 개인 binary classification의 경우에는 다음과 같은 metric이 있다.
- Classification threshold에 영향을 받는 metrics → prediction 값 결과의 범위가 \([0, 1]\)인 경우, 0.5를 threshold로 사용한다.
- Accuracy
- Precision/Recall
- Classification threshold에 영향을 받지 않는 metrics
- ROC AUC
Binary Classification에 사용되는 metric들을 각각 자세히 살펴보자.
(1) Accuracy, Precision(P), Recall(R), F1 Score
Binary classification 결과 다음과 같은 confusion matrix를 얻었다고 해보자.

여기서 accuracy, precision, recall, f1 score는 각각 다음과 같이 구한다.
- Accuracy : 일반적인 정확도이다. 전체 데이터 중 맞게 분류한 data의 비율이다.
- \( \cfrac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}} = \cfrac{\text{TP} + \text{TN}}{\lvert \text{Dataset} \rvert} \)
- Precision (P) : positive로 예측한 것 중 진짜 positive인 data의 비율을 말한다.
- \( \cfrac{\text{TP}}{\text{TP} + \text{FP}} \)
- Recall (R) : 실제로 positive인 것 중 positive로 예측한 data의 비율을 말한다.
- \( \cfrac{\text{TP}}{\text{TP} + \text{FN}} \)
- F1 score : Precision과 Recall로 계산한 정확도 개념이다.
- \( \cfrac{2 P R}{P + R} \)
(2) ROC(Reciever Operating Characteristic) Curve, ROC AUC(Area Under the ROC Curve)
ROC curve는 binary classifier의 classification threshold의 변화에 따른 TPR(Recall)과 FPR의 trade-off 관계를 파악하기 위한 curve이다.
클래스 별로 분포가 다를 때(imbalance data일 때), accuracy의 단점을 해결한 분류 성능 지표이다.
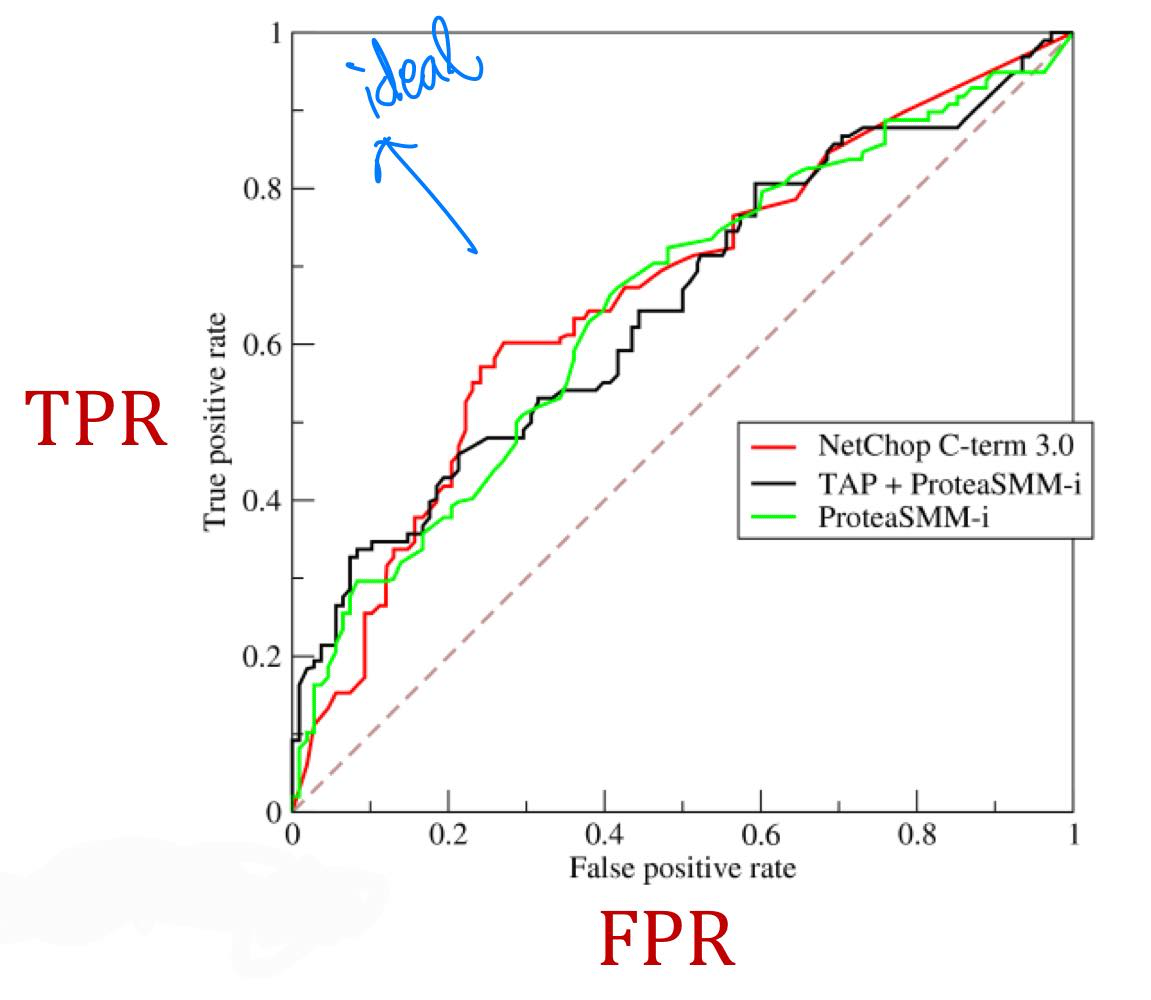
- TPR (True Positive Rate, Recall) : 실제 positive data 중 positive로 예측한 data의 비율
- \( \cfrac{\text{TP}}{\text{TP} + \text{FN}} \)
- FPR (False Positive Rate) : 실제 negative data 중 positive로 예측한 data의 비율
- \( \cfrac{\text{FP}}{\text{FP} + \text{TN}} \)
점선은 random classifier의 성능을 나타낸다. 즉 점선에서 멀수록 좋은 binary classifier이다.
ROC AUC는 ROC curve 아래의 면적을 나타낸다. 이는 random으로 positive 데이터와 negative 데이터를 하나씩 골랐을 때, classifier가 제대로 분류할 확률이다. 이상적인 경우 AUC = 1('ㄱ'자 형태의 그래프), 최악의 경우 AUC = 0.5(점선)이다. 완전히 랜덤으로 positive/negative를 분류할 때(최악일 때) 0.5, negative는 negative로, positive는 positive로 분류할 때 1의 값을 보일 것이다.
이상으로 GNN을 학습하는 전반적인 과정, 특히 node embedding을 구한 이후로 prediction, loss 설정, evaluation을 어떻게 진행하는지를 모두 살펴보았다.








최근댓글