Visual Odometry (2) - 2D-2D Epipolar Geometry

Xiang Gao, Tao Zhang 저자의 'Introduction to Visual SLAM from Theory to Practice' 책을 통해 SLAM에 대해 공부한 내용을 기록하고자 한다.

책의 내용은 주로 'SLAM의 기초 이론', 'system architecture', 'mainstream module'을 다룬다.

 

포스팅에는 기초 이론만 다룰 것이며, 실습을 해보고 싶다면 다음 github를 참조하자.

 

https://github.com/gaoxiang12/slambook2

GitHub - gaoxiang12/slambook2: edition 2 of the slambook

 

Visual Odometry 이전 과정인 feature extraction 및 feature matching 과정에 대한 내용은 다음 글을 참조하자.

 

https://jjuke-brain.tistory.com/entry/Visual-Odometry-1-ORB-Feature-Feature-Matching

Visual Odometry (1) - Feature Method, ORB Feature, Feature Matching

 

 

목차

 

 

 

이전 포스팅에서 feature extraction, feature matching에 대해 알아보았다.

Feature matching 결과는 카메라의 motion을 추정하는 데 쓰인다.

Motion estimation 방법은 어떤 카메라를 사용하는지 혹은 카메라의 설정에 따라 3가지로 나뉜다고 하였다.

그중 이번에는 2D-2D case를 다루어볼 것이다.

 

 

 

2D-2D: Epipolar Geometry

 

 

 

 

Epipolar Constraints

 

두 이미지에서 매칭된 feature point 쌍의 일치성을 통해 두 프레임 간에 카메라가 어떻게 움직였는지를 알아낼 수 있다.

간단한 예시를 통해 알아보자.

 

Epipolar Constraints

 

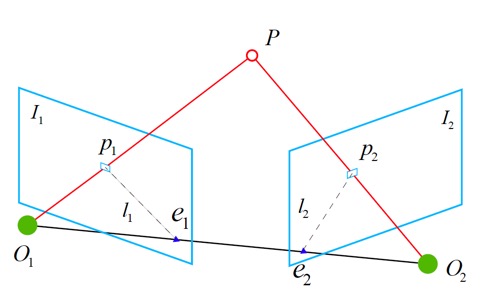
목표는 image plane \(I_1, I_2\) 사이에 카메라의 motion을 찾는 것이다.

이때 카메라의 motion은 \(\mathbf{R, t}\)로 생각할 수 있다. (자세한 내용은 링크를 참조하자.)

각 image를 얻을 때의 카메라의 중심은 \(O_1, O_2\)이고, \(I_1, I_2\)에서 서로 일치하는 feature point는 각각 \(p_1, p_2\)이다. 매칭이 제대로 됐다면, 두 점은 서로 같은 점의 projection일 것이다.

\(P\)는 직선 \(\overrightarrow{O_1 p_1}\)과 직선 \(\overrightarrow{O_2 p_2}\)가 교차하는 3차원 상의 점이다.

 

이때, 세 점 \(O_1, O_2, P\)가 만드는 평면을 epipolar plane이라 한다.

그리고 직선 \(\overrightarrow{O_1 O_2}\)를 baseline이라 하고, 이 basline과 image plane \(I_1, I_2\)가 만나는 점을 각각 \(e_1, e_2\)로 두며, 이를 epipole이라 한다.

그리고 polar plane과 image plane이 교차하는 직선 \(l_1, l_2\)를 epipolar line이라 한다.

 

첫 번째 frame에서, 반직선 \(\overrightarrow{O_1 p_1}\)상의 모든 점이 같은 픽셀 \(p_1\)에 투영된다. 즉, point \(P\)가 직선 \(\overrightarrow{O_1 p_1}\) 상의 어딘가에 존재하고 있다는 것을 말한다.

\(P\)의 위치를 모른다 가정하고 두 번째 frame을 보면, epipolar line인 \(\overrightarrow{e_2 p_2}\)는 point \(P\)가 \(I_2\)에 투영될 수 있는 위치를 나타낸다.

그런데 feature matching을 통해 \(p_2\)의 위치를 결정했으므로, \(P\)의 위치를 알 수 있게 된다.

이를 통해 최종적으로 카메라의 움직임도 추론하게 될 것이다.

 

 

 

Epipolar Constraint 유도 과정

 

첫 번째 프레임에서의 \(P\)의 위치를 다음과 같이 나타내자.

 

\( \mathbf{P} = \left[ X, Y, Z \right]^T\)

 

Pinhole camera model을 사용하여 다음과 같이 pixel position을 나타낼 수 있다.

(Pinhole camera model의 자세한 내용은 링크를 참조하자.)

 

\( s_1 \mathbf{p}_1 = \mathbf{KP}, \quad s_2 \mathbf{p}_2 = \mathbf{K}(\mathbf{RP} + \mathbf{t}) \)

 

이때 \( \mathbf{K}\)는 카메라의 intrinsic matrix, \(\mathbf{R, t}\)는 두 프레임 사이에서 카메라의 움직임이다. (첫 번째에서 두 번째 프레임으로의 transformation은 정확히 \(\mathbf{R_{21}, t_{21}}\)로 표현한다. 물론 Lie Algebra 형태로도 나타낼 수 있다.)

또한, Homogeneous coordinate를 사용하면 벡터에 0이 아닌 상수를 곱해도 원래 벡터와 같게 된다. 따라서 projection relationship을 나타내기 좋다. 이를 'equal up to a scale'이라고 표현하고, 수식으로 나타내면 다음과 같다.

 

\(s \mathbf{p} \simeq \mathbf{p} \)

 

이를 pinhole camera model에 적용하면 다음과 같이 표현이 가능하다.

 

\( \mathbf{p}_1 \simeq \mathbf{KP}, \quad \mathbf{p}_2 \simeq \mathbf{K} ( \mathbf{RP} + \mathbf{t} ) \)

 

두 픽셀 \(p_1, p_2\)의 normalized plane 상의 좌표를 \(\mathbf{x}_1, \mathbf{x}_2\)라 하면 \(\mathbf{x}_1 = \mathbf{K}^{-1} \mathbf{p}_1, \quad \mathbf{x}_2 = \mathbf{K}^{-1} \mathbf{p}_2\)를 만족하고, 이를 식에 대입하면

 

\( \mathbf{x}_2 \simeq \mathbf{R} \mathbf{x}_1 + \mathbf{t} \)

 

양변을 \(\mathbf{t}\)로 outer product하면, (즉, 좌측에 \(\mathbf{t}^\wedge\)를 곱해주면) 자신과의 외적은 영벡터이므로 다음과 같아진다.

 

\( \mathbf{t}^\wedge \mathbf{x}_2 \simeq \mathbf{t}^\wedge \mathbf{R} \mathbf{x}_1 \)

 

다시 왼쪽에 \(\mathbf{x}_2^T\)를 곱해주면

 

\( \mathbf{x}_2^T \mathbf{t}^\wedge \mathbf{x}_2 \simeq \mathbf{x}_2^T \mathbf{t}^\wedge \mathbf{R} \mathbf{x}_1 \)

 

이와 같은 형태의 식을 유도할 수 있다.

여기서 좌변의 \(\mathbf{t}^\wedge \mathbf{x}_2\)는 \(\mathbf{t}\)와 \(\mathbf{x}_2\) 두 벡터에 직교하는 벡터이므로 \(\mathbf{x}_2\)와의 내적 결과는 0일 것이다.

이에 따라 식의 좌변이 strictly zero (정확하게 0)이 되므로, 0이 아닌 상수를 곱해도 여전히 0이 되고, 따라서 \(\simeq\) symbol을 \(=\)으로 바꿀 수 있다.

따라서 다음 식을 얻게 되고,

 

\( \mathbf{x}_2^T \mathbf{t}^\wedge \mathbf{R} \mathbf{x}_1 = 0 \)

 

\( \mathbf{p}_1, \mathbf{p}_2\)를 다시 대입하면 다음 식을 얻는다.

 

\( \mathbf{p}_2^T \mathbf{K}^{-T} \mathbf{t}^\wedge \mathbf{R} \mathbf{K}^{-1} \mathbf{p}_1 = 0 \)

 

위 두 식 모두 epipolar constraint이다.

 

 

 

Epipolar Constraint의 특징

 

기하학적으로 보면, \(O_1, O_2, P\)는 coplanar(같은 평면 위의 점)이다.

또한 식에서도 알 수 있듯이, epipolar constraint는 translation과 rotation 둘 다 encoding한다.

그리고 이 식에서 나타나는 중요한 두 matrix를 정의한다.

1. Essential Matrix : \( \mathbf{E} = \mathbf{t}^\wedge \mathbf{R} \)
2. Fundamental Matrix : \( \mathbf{F} = \mathbf{K}^{-T} \mathbf{E} \mathbf{K}^{-1} \)

 

따라서 epipolar constraint를 위 matrix로 정의하면 다음과 같다.

 

\( \mathbf{x}_2^T \mathbf{E} \mathbf{x}_1 = \mathbf{p}_2^T \mathbf{F} \mathbf{p}_1 = 0 \)

 

Epipolar constraint를 통해 우리는 두 matching point의 공간적인 관계를 알 수 있다.

따라서 camera pose estimation 문제는 다음 두 단계로 간단히 요약할 수 있다.

1. 매칭된 point의 픽셀 위치에 기반하여 \(\mathbf{E}\) 혹은 \(\mathbf{F}\)를 찾는다.
2. 찾은 \(\mathbf{E}\)나 \(\mathbf{F}\)로 \(\mathbf{R, t}\)를 찾는다.

 

\(\mathbf{E}\)와 \(\mathbf{F}\)의 차이점은 식에서 internal parameter의 존재 유무이다.

SLAM task에서는 internal parameter는 알고있다고 가정하기 때문에, 더 간단한 형태인 \(\mathbf{E}\)를 많이 사용한다.

그럼 essential matrix에 대해 좀 더 자세히 살펴보자.

 

 

 

 

Essential Matrix \(\mathbf{E}\)

 

정의에 따르면, essential matrix는 크기가 3 × 3인 행렬이고, \(\mathbf{E} = \mathbf{t}^\wedge \mathbf{R}\)을 만족한다. 즉, 9개의 미지수가 존재한다.

또한 다음과 같은 특징을 갖는다.

• 서로 다른 scale에 대한 equivalence
  • Essential matrix는 epipolar constraint에 의해 정의되는데, epipolar constraint는 '... = 0 (equal-to-zero)' 형태의 식이므로 0이 아닌 상수를 곱해도 성립한다.
  • 따라서 scale이 달라져도 \(\mathbf{E}\)는 동일하다.
• Internal properties
  • 정의에 따라 \(\mathbf{E}\)의 singular value는 \(\left[ \sigma, \sigma, 0 \right]^T\)의 형태를 갖는다. (자세한 증명은 생략한다.)
• Translation과 rotation은 3DoF를 갖기 때문에, \(\mathbf{t}^\wedge \mathbf{R}\)인 essential matrix는 6DoF를 갖게 된다. 하지만, scale에 대한 equivalence 성질을 가지므로 5DoF를 갖는다.

 

Essential matrix \(\mathbf{E}\)가 5DoF를 가진다는 것은 \(\mathbf{E}\)를 구하기 위해 5쌍의 points가 필요하다는 것을 의미한다.

하지만, internal property가 nonlinear이기 때문에, \(\mathbf{E}\)를 구할 때에는 scale equivalence만 고려하여 매칭된 점의 쌍 8개를 사용한다. 즉, 총 9개 미지수(3 × 3 matrix)를 구해야 하지만 scale equivalence를 고려하여 하나를 뺀 8개 필요하다는 것이다.

이를 eight-point-algorithm이라 한다.

 

 

 

Eight-point method

 

Eight-point-algorithm은 \(\mathbf{E}\)의 선형적 성질만 사용하므로 선형대수를 사용할 수 있다.

 

매칭된 점 한 쌍이 있다고 가정하자. 이들의 normalized coordinate는 각각 \(\mathbf{x}_1 = \left[ u_1, v_1, 1 \right]^T\), \( \mathbf{x}_2 = \left[ u_2, v_2, 1 \right]^T \)이다.

Polar constraint에 대입하면 다음을 만족한다.

 

\( \begin{pmatrix} u_2 & v_2 & 1 \end{pmatrix} \begin{pmatrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{pmatrix} \begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} = 0\)

 

\( \mathbf{E}\)를 벡터 형태로 \(\mathbf{e} = \left[ e_1, e_2, e_3, e_4, e_5, e_6, e_7, e_8, e_9 \right]^T \)로 나타내면, epipolar constraint는 \(\mathbf{e}\)에 대한 linear form으로 다음과 같이 쓸 수 있다.

 

\( \left[ u_2u_1, u_2v_1, u_2, v_2u_1, v_2v_1, v_2, u_1, v_1, 1 \right] \cdot \mathbf{e} = 0 \)

 

i번째 feature point 쌍을 \((u^i, v^i)\)로 둔다면, 8개의 point 쌍에 대한 식을 다음 linear equation system으로 나타낼 수 있다.

 

\( \begin{pmatrix} u_2^1u_1^1 & u_2^1v_1^1 & u_2^1 & v_2^1u_1^1 & v_2^1v_1^1 & v_2^1 & u_1^1 & v_1^1 & 1 \\ u_2^2u_1^2 & u_2^2v_1^2 & u_2^2 & v_2^2u_1^2 & v_2^2v_1^2 & v_2^2 & u_1^2 & v_1^2 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ u_2^8u_1^8 & u_2^8v_1^8 & u_2^8 & v_2^8u_1^8 & v_2^8v_1^8 & v_2^8 & u_1^8 & v_1^8 & 1 \end{pmatrix} \begin{pmatrix} e_1 \\ e_2 \\ e_3 \\ e_4 \\ e_5 \\ e_6 \\ e_7 \\ e_8 \\ e_9 \end{pmatrix} = 0 \)

 

위 linear equation system의 계수행렬(coefficient matrix)은 2D feature point의 위치(좌표)로 구성되며, 사이즈는 8 × 9이다.

\(\mathbf{e}\)는 이 행렬의 null space에 위치하며(즉, 계수행렬을 \(\mathbf{C}\)라 하면 \(\mathbf{Ce = 0}\)을 만족한다는 의미이므로 위 식과 의미가 같다), coefficient matrix가 full rank(8)일 경우 null space의 차원이 1이 되면서 \(\mathbf{e}\)는 직선이 된다.

이 말은 곧 \(\mathbf{e}\)의 scale equivalence성질과 일맥상통한다. 8쌍의 matching point로 구성된 행렬의 rank가 8인 경우, \(\mathbf{E}\)의 요소들은 위 식에 의해 유일한 해를 얻는다는 의미이기 때문이다.

 

Internal property를 굳이 사용하여 5DoF를 갖게 될 수도 있으나, 계산이 매우 복잡해지고, 실제로는 수많은 feature points 쌍을 얻을 수 있으므로, 8개 쌍을 얻을 때에 비해 5개 쌍을 얻을 때가 큰 이점이 없다.

따라서 선형으로 비교적 간단히 구할 수 있기 때문에 일반적으로 eight-point-algorithm을 사용한다.

 

다음으로는 드디어 카메라의 움직임, 즉 \(\mathbf{R, t}\)를 구하는 방법을 알아볼 것이다.

 

 

 

 

Essential matrix로부터 카메라의 움직임 구하기

 

\(\mathbf{E}\)로 카메라의 움직임을 구하는 핵심 아이디어는 바로 SVD(Singular Value Decomposition)이다.

\(\mathbf{E}\)의 SVD는 다음과 같다.

 

\( \mathbf{E} = \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^T \)

 

여기서 \(\mathbf{U, V}\)는 orthogonal matrices, \(\boldsymbol{\Sigma}\)는 singular value matrix이다.

\( \mathbf{E}\)의 internal property에 의하면 \(\boldsymbol{\Sigma} = \operatorname{diag} \left( \sigma, \sigma, 0 \right)\)이고, SVD를 통해 어떤 \(\mathbf{E}\)에 대해서도 다음 두 식을 만족하는 \(\mathbf{t, R}\) 행렬을 얻을 수 있다.

 

\( \begin{cases} \mathbf{t}_1^\wedge = \mathbf{U} \mathbf{R}_Z \left( \cfrac{\pi}{2} \right) \boldsymbol{\Sigma} \mathbf{U}^T, \quad \quad \mathbf{R}_1 = \mathbf{U} \mathbf{R}_Z^T \left( \cfrac{\pi}{2} \right) \mathbf{V}^T \\ \mathbf{t}_2^\wedge = \mathbf{U} \mathbf{R}_Z \left( - \cfrac{\pi}{2} \right) \boldsymbol{\Sigma} \mathbf{U}^T, \quad \quad \mathbf{R}_2 = \mathbf{U} \mathbf{R}_Z^T \left( - \cfrac{\pi}{2} \right) \mathbf{V}^T \end{cases} \)

 

여기서 \(\mathbf{R_Z} \left( \cfrac{\pi}{2} \right) \)는 Z축에 대해 \(90^\circ\) 회전하여 얻은 rotation matrix를 나타낸다.

\(\mathbf{E} = - \mathbf{E}\)이므로, \(\mathbf{t}\)에 -를 붙여도 같은 결과를 얻게 되므로, SVD 과정을 통해 총 4가지 가능한 해를 얻게 된다.

 

Four Solutions when Decomposing the Essential Matrix

 

빨간 점으로 표시된 projected point(\(p_1, p_2\))를 알고 있으며, 이를 통해 카메라의 움직임을 구하는 과정을 알아보고 있다.

위와 같이 4가지 가능한 경우가 생기는데, 4가지 중 depth값(distance)이 두 카메라의 중점 \(O_1, O_2\)에서 모두 양수인 경우는 첫 번째 그림이 유일하다. 상식적으로 Image plane은 카메라 앞에 생기므로, 최종 solution은 (1)이다.

 

그런데, linear equation으로 구한 \(\mathbf{E}\)는 internal property를 만족하지 않을 수 있다. (즉, singular value matrix의 형태가 \( \left[ \sigma, \sigma, 0 \right]^T \)의 형태가 아닐 수 있다.)

이 때에는 \(\boldsymbol{\Sigma}\)를 직접 조정하여 위와 같은 형식이 되도록 한다.

 

\( \mathbf{E} = \mathbf{U} \operatorname{diag}{\left( \cfrac{\sigma_1 + \sigma_2}{2}, \; \cfrac{\sigma_1 + \sigma_2}{2}, \; 0 \right)} \mathbf{V}^T \)

 

기하학적으로 보면, linear equation으로 구한 해를 실제 \(\mathbf{E}\)가 위치하는 manifold 상으로 투영시키는 것을 나타낸다.

또한, \( \mathbf{E}\)는 scale equivalence 특성을 가지므로, singular value matrix로 \(\operatorname{diag}{(1, 1, 0)}\)을 취하면 더 간단히 구할 수 있다.

 

 

 

 

Homography

 

Fundamental matrix와 essential matrix 말고도 two-view geometry에서 또다른 common matrix가 있는데, 바로 homography matrix \(\mathbf{H}\)이다.

이는 두 평면간의 mapping 관계를 나타낸다. Image formation 중 Perspective Transformation에서 이 행렬을 본 적이 있을 것이다.

(이미지의 formation의 종류를 알고싶다면 링크를 참조하자.)

 

Scene에서의 feature point가 모두 같은 평면에 존재할 때, (예를 들어 wall, ground 등) 이 행렬을 사용하여 카메라의 motion을 추정할 수 있다.

 

표현은 약간 다르지만, OpenCV 공식 문서에 소개된 다음 그림을 참조하자.

 

Homography

 

이미지 \(I_1, I_2\)에서 매칭된 feature point \(p_1, p_2\)가 plane \(P\) 상에 존재한다고 가정하면, normal vector \(\mathbf{n}\)에 대해 다음 평면방정식이 성립한다.

 

\( \mathbf{n}^T \mathbf{P} + d = 0 \)

\( \therefore - \cfrac{\mathbf{n}^T \mathbf{P}}{d} = 1 \)

 

Pinhole camera model에 따라 다음이 성립한다.

 

\( \begin{align*} \mathbf{p}_2 & \simeq \mathbf{K} (\mathbf{RP} + \mathbf{t}) \\ & \simeq \mathbf{K} \left( \mathbf{RP} + \mathbf{t} \cdot \left( - \cfrac{\mathbf{n}^T \mathbf{P}}{d} \right) \right) \\ & \simeq \mathbf{K} \left( \mathbf{R} - \cfrac{\mathbf{t} \mathbf{n}^T}{d} \right) \mathbf{P} \\ & \simeq \mathbf{K} \left( \mathbf{R} - \cfrac{\mathbf{t} \mathbf{n}^T}{d} \right) \mathbf{K}^{-1} \mathbf{p}_1 \end{align*} \)

 

여기서 \( \mathbf{K} \left( \mathbf{R} - \cfrac{\mathbf{t} \mathbf{n}^T}{d} \right) \mathbf{K}^{-1} \mathbf{P} \)를 \(\mathbf{H}\)로 정의한다. 이에 따라 \(p_1, p_2\)간의 transformation을 다음과 같이 간단히 나타낼 수 있다.

 

\( \mathbf{p}_2 \simeq \mathbf{H} \mathbf{p}_1 \)

 

\(\mathbf{H}\)는 perspective transformation, 즉 transformation 중 가장 일반적인 형태이다. 즉, rotation, translation, plane coefficients 등의 parameter를 갖는다.

또한 3 × 3 크기를 갖고, essential matrix에서와 마찬가지로 matching points쌍을 통해 이 행렬을 계산한 후 SVD를 적용하여 rotation과 translation을 찾을 수 있다.

 

위 식을 풀어쓰면 다음과 같다.

 

\( \begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} \simeq \begin{pmatrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \end{pmatrix} \begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} \)

 

Homogeneous coordinates에서 non-homogeneous coordinates로 변환하는 과정을 살펴보자.

 

\( \begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} \simeq \begin{pmatrix} h_1u_1 + h_2v_1 + h_3 \\ h_4u_1 + h_5v_1 + h_6v_1 \\ h_7u_1 + h_8 v_1 + h_9 \end{pmatrix} \)

 

\( \begin{cases} u_2 = \cfrac{h_1 u_1 + h_2 v_1 + h_3}{h_7 u_1 + h_8 v_1 + h_9} \\ v_2 = \cfrac{h_4 u_1 + h_5 v_1 + h_6}{h_7 u_1 + h_8 v_1 + h_9} \end{cases} \)

 

equal sign이 \(\simeq\)이므로, \(\mathbf{H}\) 행렬 또한 0이 아닌 상수를 곱할 수 있다.

보통 \(h_9\) 값이 0이 아니라면 이 값을 1로 만들어 normalize해준다.

이에 따라 정리하면,

 

\( \begin{cases} h_1u_1 + h_2v_1 + h_3 - h_7u_1u_2 - h_8v_1u_2 = u_2 \\ h_4u_1 + h_5v_1 + h_6 - h_7u_1v_2 - h_8v_1v_2 = v_2 \end{cases} \)

 

Matching points 한 쌍이 두 개의 constraints를 구성할 수 있으므로, 8DoF를 갖는 \(\mathbf{H}\)는 매칭된 feature point 쌍 4개로 다음 linear equation system을 풀어서 구할 수 있다.

 

\( \begin{pmatrix} u_1^1 & v_1^1 & 1 & 0 & 0 & 0 & -u_1^1 u_2^1 & -v_1^1 u_2^1 \\ 0 & 0 & 0 & u_1^1 & v_1^1 & 1 & -u_1^1 v_2^1 & -v_1^1 v_2^1 \\ u_1^2 & v_1^2 & 1 & 0 & 0 & 0 & -u_1^2 u_2^2 & -v_1^2 u_2^2 \\ 0 & 0 & 0 & u_1^2 & v_1^2 & 1 & -u_1^2 v_2^2 & -v_1^2 v_2^2 \\ u_1^3 & v_1^3 & 1 & 0 & 0 & 0 & -u_1^3 u_2^3 & -v_1^3 u_2^3 \\ 0 & 0 & 0 & u_1^3 & v_1^3 & 1 & -u_1^3 v_2^3 & -v_1^3 v_2^3 \\ u_1^4 & v_1^4 & 1 & 0 & 0 & 0 & -u_1^4 u_2^4 & -v_1^4 u_2^4 \\ 0 & 0 & 0 & u_1^4 & v_1^4 & 1 & -u_1^4 v_2^4 & -v_1^4 v_2^4 \end{pmatrix} \begin{pmatrix} h_1 \\ h_2 \\ h_3 \\ h_4 \\ h_5 \\ h_6 \\ h_7 \\ h_8 \end{pmatrix} = \begin{pmatrix} u_2^1 \\ v_2^1 \\ u_2^2 \\ v_2^2 \\ u_2^3 \\ v_2^3 \\ u_2^4 \\ v_2^4 \end{pmatrix} \)

 

이 식은 위의 \(\mathbf{E}\) (essential matrix)에서와 마찬가지로 \(\mathbf{H}\) 행렬을 vector로 간주하여 풀어 쓴 것이다. 이러한 방법을 Direct Linear Transform (DLT)라 한다.

위 식에서 coefficient matrix가 나오므로 SVD를 통해 \(\mathbf{R, t}\)를 구할 수 있다.

4가지 solution이 나오게 되는데, depth 값이 모두 양수인 경우를 통해 2가지를 제외시키고, scene plane의 normal vector \(\mathbf{n}\)을 알고 있으므로 이를 통해 최종 해를 구할 수 있다. (만약 scene plane이 camera plane과 평행하다면 normal vector \(\mathbf{n}\)은 \(\boldsymbol{1}^T\)일 것이다.)

 

 

Feature point들이 모두 같은 평면에 위치하는 경우, 카메라는 pure rotation만 하게 되고, fundamental matrix \(\mathbf{F}\)의 DoF가 줄어들어 degeneration이 발생한다. 즉, eight-point method만 사용한다면 degeneration 문제가 발생한다.

(Degeneration이란, 실제 데이터에 존재하는 noise에 의해 redundant freedom이 결정되는 현상을 말한다.)

 

따라서 eight-point method와 homography를 둘 다 사용하여 motion을 추정해보고, 더 작은 reprojection error를 갖는 결과를 최종적으로 선택해야 할 것이다.