Xiang Gao, Tao Zhang 저자의 'Introduction to Visual SLAM from Theory to Practice' 책을 통해 SLAM에 대해 공부한 내용을 기록하고자 한다.
책의 내용은 주로 'SLAM의 기초 이론', 'system architecture', 'mainstream module'을 다룬다.
포스팅에는 기초 이론만 다룰 것이며, 실습을 해보고 싶다면 다음 github를 참조하자.
https://github.com/gaoxiang12/slambook2
GitHub - gaoxiang12/slambook2: edition 2 of the slambook
edition 2 of the slambook. Contribute to gaoxiang12/slambook2 development by creating an account on GitHub.
github.com
목차
우리가 다루게 될 카메라, 로봇 몸체 등은 모두 Rigid body이고, 이것은 position과 orientation을 갖는다.
이번 포스팅에서는 Rigid Body의 중요한 특성인 position과 orientation을 어떻게 수학적으로 표현할 수 있는지 알아볼 것이다.
그 전에, 기본적인 개념을 어떻게 표현할지 알아보자. 표현은 책마다 조금씩 다를 수 있다.
먼저, 벡터는 bold체로 \(\boldsymbol{a}\)로 나타내며, base는 \(\boldsymbol{e}\)로 다음과 같이 표현한다.
\( \boldsymbol{a} = \left[ \boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3 \right] \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = a_1 \boldsymbol{e}_1 + a_2 \boldsymbol{e}_2 + a_3 \boldsymbol{e}_3 \)
여기서 \( \left( a_1, a_2, a_3 \right)^T \)는 \( \boldsymbol{a}\)의 coordinate이다.
또한 두 벡터의 Inner Product는 다음과 같이 표현한다.
\( \boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{a}^T \boldsymbol{b} = \overset{3}{\underset{i=1}{\sum}} a_i b_i = \left| \boldsymbol{a} \right| \left| \boldsymbol{b} \right| \cos \langle \boldsymbol{a}, \boldsymbol{b} \rangle \)
여기서 \(\langle \boldsymbol{a}, \boldsymbol{b} \rangle\)이란, 두 벡터 사이의 각도를 말한다.
두 벡터의 Outer Product는 다음과 같이 표현한다.
\( \boldsymbol{a} \times \boldsymbol{b} = \begin{vmatrix} \boldsymbol{e}_1 & \boldsymbol{e}_2 & \boldsymbol{e}_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \begin{bmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{bmatrix} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \boldsymbol{b} \triangleq \boldsymbol{a}^\wedge \boldsymbol{b} \)
여기서 \( ^\wedge \) operator는 skew-symmetric matrix ( \(A^T = -A \)인 Matrix)를 나타낸다.
\( \boldsymbol{a}^\wedge = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \)
Rotation Matrix, Translation Vector, Transformation Matrix
로보틱스 분야에서는 각 link와 joint마다 coordinate system을 정의한다.
움직이는 로봇을 떠올려보자. 보통 움직이지 않는 inertial coordinate system(world coordinate system)을 \(x_W, y_W, z_W\)와 같이 설정한다. 반면, 카메라나 로봇은 움직이는 coordinate system(예를 들어 \(x_C, y_C, z_C\))을 갖게 된다.
이때 어떤 vector \(\boldsymbol{p}\)는 카메라 system에서는 \(\boldsymbol{p}_c\)로, world coordinate system에서는 \(\boldsymbol{p}_w\)로 표현될 것인데, 카메라에 대해 \(\boldsymbol{p}_c\)를 얻은 다음 coordinate transform을 적용하여 \(\boldsymbol{p}_w\)를 얻어내는 계산이 필요한 경우가 많다.
따라서 수학적으로 이러한 좌표계의 transformation을 정의해주어야 하는데, 이때 transform matrix \(\boldsymbol{T}\)를 사용한다.
직관적으로, 두 좌표계 간의 변화는 회전(rotation)과 병진(translation)의 합으로 나타낼 수 있다. 이를 Rigid Body Motion이라 한다.
Rigid Body Motion (좌표계 변환) 도중에는 어떤 벡터의 크기나 각이 변하지 않으므로, 이러한 rigid body의 motion은 Euclidean이라 말할 수 있다.
따라서 Euclidean Transform은 Rotation과 Translation을 포함한다. 먼저 Rotation부터 알아보자.
Rotation Matrix
크기가 1인 orthogonal base \( (\boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3 ) \)을 회전시켜 \((\boldsymbol{e}_1', \boldsymbol{e}_2', \boldsymbol{e}_3' )\)로 변환한다고 하자.
또한, 어떤 벡터 \(\boldsymbol{a}\)를 두 좌표계에서 각각 \(\left[ a_1, a_2, a_3\right]^T\), \(\left[a_1', a_2', a_3' \right]^T\)로 나타낸다.
벡터 \(\boldsymbol{a}\)는 바뀌지 않기 때문에, 다음이 성립한다.
\([\boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3] \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = [\boldsymbol{e}_1', \boldsymbol{e}_2', \boldsymbol{e}_3'] \begin{bmatrix} a_1' \\ a_2' \\ a_3' \end{bmatrix} \)
base component 스스로의 내적 값은 1, 나머지 component와의 내적 값은 0(직교하므로)이므로, 양변에 \(\begin{bmatrix} \boldsymbol{e}_1^T \\ \boldsymbol{e}_2^T \\ \boldsymbol{e}_3^T \end{bmatrix}\)를 곱해주면 다음과 같은 식을 얻을 수 있다.
\( \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} \boldsymbol{e}_1^T \boldsymbol{e}_1' & \boldsymbol{e}_1^T \boldsymbol{e}_2' & \boldsymbol{e}_1^T \boldsymbol{e}_3' \\ \boldsymbol{e}_2^T \boldsymbol{e}_1' & \boldsymbol{e}_2^T \boldsymbol{e}_2' & \boldsymbol{e}_2^T \boldsymbol{e}_3' \\ \boldsymbol{e}_3^T \boldsymbol{e}_1' & \boldsymbol{e}_3^T \boldsymbol{e}_2' &\boldsymbol{e}_3^T \boldsymbol{e}_3' \end{bmatrix} \begin{bmatrix} a_1' \\ a_2' \\ a_3' \end{bmatrix} \triangleq \boldsymbol{R} \boldsymbol{a}' \)
위 식에서 matrix \(\boldsymbol{R}\)을 Rotation Matrix라 한다.
또한 base vector의 크기는 1이기 때문에, 두 coordinate system의 base의 내적은 두 base vector의 사이각의 코사인 값이다. 따라서 이를 direction cosine matrix라고 부르기도 한다.
Rotation Matrix는 determinant가 1이고, orthogonal matrix라는 특성을 갖는다. (역도 성립한다.) 따라서 이후에 배울 "Group"의 개념을 사용하여 special orthogonal group으로 다음과 같이 나타낼 수 있다.
\( \text{SO}(n) = \left\{ \boldsymbol{R} \in \mathbb{R}^{n \times n} | \boldsymbol{R}\boldsymbol{R}^T = \boldsymbol{I}, \text{det}(\boldsymbol{R}) = 1 \right\} \)
여기서 \(n\)은 차원으로, 3차원이라면 \(\text{SO}(3)\)으로 표현한다.
Rotation Matrix는 orthogonal이기 때문에, inverse(=transpose)로 반대 방향 회전을 정의할 수 있다.
\( \boldsymbol{a} = \boldsymbol{R} \boldsymbol{a}' \Rightarrow \boldsymbol{a}' = \boldsymbol{R}^{-1} \boldsymbol{a} = \boldsymbol{R}^T \boldsymbol{a} \)
Translation Vector
Euclidean transformation에서는 rotation이외에 translation이 존재한다고 했다. 이는 간단히 translation vector \(\boldsymbol{t}\)를 더하여 다음과 같이 나타낼 수 있다.
\( \boldsymbol{a}' = \boldsymbol{R} \boldsymbol{a} + \boldsymbol{t} \)
여기서 \(\boldsymbol{t}\)를 translation vector라 한다. rotation과 비교하면 translation은 단순히 각 벡터의 요소를 더하는 것이 translation이므로, 벡터로 생각할 수 있다.
실제로는 coordinate system 1, 2에 대해 vector \( \boldsymbol{a}\)는 각각 \( \boldsymbol{a}_1, \boldsymbol{a}_2 \)로 나타낼 수 있으므로, system 2에서 system 1로 rotation 및 translation 변환하는 과정은 다음과 같이 나타낼 수 있다.
\( \boldsymbol{a}_1 = \boldsymbol{R}_{12} \boldsymbol{a}_2 + \boldsymbol{t}_{12} \)
표현은 책마다 다를 수 있는데, 여기서는 coordinate 2에서 1로 rotation 또는 translation할 경우 아래첨자에 '12'로 표시하였다.
한 가지 유의할 점은, rotation matrix의 경우 여러 번의 coordinate 변화가 일어났을 때 단순히 곱하여서 회전을 정의할 수 있으나, translation vector의 경우에는 coordinate 변화가 여러 번 일어날 때 회전도 함께 고려해주어야 한다는 점이다. (자세한 증명은 다루지 않겠다.)
\( \boldsymbol{R}_{31} = \boldsymbol{R}_{21} \boldsymbol{R}_{32} \)
\( \boldsymbol{t}_{31} \neq \boldsymbol{t}_{21} + \boldsymbol{t}_{32} \)
Transform Matrix and Homogeneous Coordinates
동차 좌표계(Homogeneous Coordinates)란, n차원 공간을 n+1개의 좌표로 나타내는 좌표계이다.
'2)'에서의 수식은 여러 번의 transformation을 표현하기에는 (곱과 합이 함께 있기 때문에) 깔끔하지 않다.
따라서 동차 좌표계를 활용하여 transformation matrix를 다음과 같이 정의해줄 수 있다.
\( \begin{bmatrix} \boldsymbol{a}^\prime \\ 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{R} & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \begin{bmatrix} \boldsymbol{a} \\ 1 \end{bmatrix} \triangleq \boldsymbol{T} \begin{bmatrix} \boldsymbol{a} \\ 1 \end{bmatrix} \)
여기서 \(\boldsymbol{T}\)를 Transform Matrix라 한다.
동차좌표계를 사용하여 3D vector에 차원 하나를 추가함으로써 4D vector 및 matrix를 만들었고, 3차원 상의 rotation과 translation을 하나의 4차원 matrix를 사용하여 나타냈다.
또한, 왼쪽의 \(\boldsymbol{a}\)의 homogeneous coordinate에서의 표현을 \(\tilde{\boldsymbol{a}}\)로 하면, transform 과정을 다음과 같이 (행렬 표시 없이) 간단히 표현할 수 있다.
\( \tilde{\boldsymbol{b}} = \boldsymbol{T} \tilde{\boldsymbol{a}} \)
그리고 여러 번의 transform은 transform matrix들의 곱을 통해 나타낸다.
\( \tilde{\boldsymbol{b}} = \boldsymbol{T}_1 \tilde{\boldsymbol{a}}, \tilde{\boldsymbol{c}} = \boldsymbol{T}_2 \boldsymbol{T}_1 \tilde{\boldsymbol{a}} \)
tilde(~)로 매번 동차좌표계 벡터를 표현하는 것이 번거로우므로, 앞으로 해당 기호는 생략하고 간단하게 \( \boldsymbol{b} = \boldsymbol{Ta} \)와 같이 나타낼 것이다.
즉, transformation matrix를 나타낼 때(\(\boldsymbol{Ta}\))에는 \(\boldsymbol{a}\)가 homogeneous coordinate(4D), rotation matrix를 나타낼 때(\(\boldsymbol{Ra}\))에는 \(\boldsymbol{a}\)가 non-homogeneous coordinate(3D)로 생각하면 된다.
Transformation matrix \(\boldsymbol{T}\)는 특별한 구조를 갖는다.
- upper left corner (3 by 3) : Rotation matrix \(\boldsymbol{R}\)
- right side (3 by 1) : Translation vector \(\boldsymbol{t}\)
- lower left corner (1 by 3) : \(\boldsymbol{0}\) vector (행벡터이므로 위에서 transpose를 붙여주었다.)
- lower right corner (scalar) : 1
또한, Transform matrix의 집합은 다음과 같이 special Euclidean group으로 나타낼 수 있다.
\( \text{SE(3)} = \left\{ \boldsymbol{T} = \begin{bmatrix} \boldsymbol{R} & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4} | \boldsymbol{R} \in \text{SO(3)}, \boldsymbol{t} \in \mathbb{R}^3 \right\} \)
SO(3) group의 특성과 같이, transformation matrix의 inverse는 inverse transformation(역변환)을 나타낸다.
(앞서 translation vector를 역변환에서 나타낼 때에는 회전도 고려해주어야 한다고 했는데, 아래와 같은 term으로 바뀐다.)
\( \boldsymbol{T}^{-1} = \begin{bmatrix} \boldsymbol{R}^T & - \boldsymbol{R}^T \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \)
그리고 \(\boldsymbol{T}_{12}\)는 (이 책에서) 회전 변환 행렬에서와 마찬가지로 coordinate 2에서 1로 변환할 때의 변환 행렬로 표현한다.
Rotation Vectors and the Euler Angles
Rotation Vector
그럼 4 × 4 transformation matrix로 6 DoF(Degree of Freedom)의 3D rigid body motion을 완벽하게 표현할 수 있을까?
안타깝게도 그건 아니다. 행렬 표현은 다음과 같은 단점을 갖고 있다.
- Not compact
- SO(3)에서의 rotation matrix는 9개 elements(quantities)를 갖지만, 3D rotation은 3개의 DoF만 있으면 된다. 마찬가지로 transformation matrix는 6DoF 변환을 설명하기 위해 16개의 elements를 갖는다. 따라서 행렬을 활용한 표현은 redundant하다. (불필요한 요소를 추가로 갖게 된다.)
- Constraints of rotation(transformation) matrix
- 회전 변환 행렬은 determinant가 1인 orthogonal matrix여야 한다는 constraint가 있다. 이는 transformation matrix에서도 마찬가지이다. 이로 인해 estimate 또는 optimize 과정이 힘들어진다.
그러므로 좀 더 compact한 rotation 표현 방법을 찾아보자.
사실 회전은 rotation axis와 rotation angle로 나타낼 수 있다. 이에 따라 direction은 회전축과 평행하고, length는 회전 각도인 rotation vector를 고안해볼 수 있을 것이다.
이렇게 하면 3D vector로 3D 회전을 compact하게 표현할 수 있으며, rotation vector와 translation vector로 더 간단한 transformation matrix를 만들 수 있다.
회전축은 \(\boldsymbol{n}\)이라는 단위벡터이고 회전 각도는 \(\theta\)라면, vector \(\boldsymbol{n} \theta\)는 회전을 정의할 수 있다.
이렇게 정의한 회전은 rotation matrix \(\boldsymbol{R}\)과 다음의 관계가 성립한다. 즉, 서로 변환할 수 있다. 이를 Rodrigues' formula라 한다. (증명은 생략한다.)
\( \boldsymbol{R} = \cos \theta \boldsymbol{I} + (1 - \cos \theta) \boldsymbol{n} \boldsymbol{n}^T + \sin \theta \boldsymbol{n}^\wedge \)
앞서 언급했듯, \(^\wedge\) symbol은 skew-symmetric matrix를 나타낸다.
양변에 trace를 취하면 회전각을 구할 수 있고, 회전축은 회전 후에도 변하지 않으므로 다음과 같이 행렬로부터 rotation vector를 구할 수도 있다.
\( \begin{cases} \theta = \arccos \left( \frac{\text{tr} \left( \boldsymbol{R} \right) - 1}{2} \right) \\ \boldsymbol{R} \boldsymbol{n} = \boldsymbol{n} \end{cases} \)
회전축을 구하는 식을 보면, 회전축인 unit vector \(\boldsymbol{n}\)은 rotation matrix \(\boldsymbol{R}\)의 eigenvalue 1에 대한 eigenvector임을 알 수 있다.
Euler Angle
Rotation matrix나 rotation vector는 사람이 그 표현을 보고 직관적으로 어떤 회전인지 판단하기가 힘들다.
하지만 Euler angle은 3D 회전을 분해하여 세 개의 primal axes와 각각에 대한 회전 각도를 사용하여 회전을 직관적으로 묘사한다.
회전을 분해하는 여러 방법이 있는데, 각 축의 회전 순서에 따라 다른 회전을 나타낼 수 있으므로 구분이 필요하다. (표현도 매우 다양하다.)
가장 많이 사용되는 Euler Angle은 yaw-pitch-roll angles이다. 이는 Z축 기준 회전 각도를 yaw, 이후의 Y축 기준 회전 각도를 pitch, 이후의 X축 기준 회전 각도를 roll로 정한다.
축은 정하기 나름인데, 예를 들어 rigid body의 앞쪽 방향을 X축, 오른쪽 방향을 Y축, 위쪽 방향을 Z축으로 둘 수 있다.
\( \begin{cases} \theta_{\text{yaw}} = y; & \text{Rotation around the } Z \text{ axis of the object} \\ \theta_{\text{pitch}} = p; & \text{Rotation around the } Y \text{ axis of after rotation} \\ \theta_{\text{roll}} = r. & \text{Rotation around the } X \text{ axis of after rotation} \end{cases} \)
이러한 방법으로 3차원 벡터 \(\left[ y, p, r \right]^T\)를 사용하여 회전을 나타낼 수 있다.
같은 회전을 나타내더라도 축의 순서에 따라 값이 달라질 수 있다.
하지만 이러한 Euler anlge도 'Gimbal Lock 현상'이라는 단점을 갖는다.
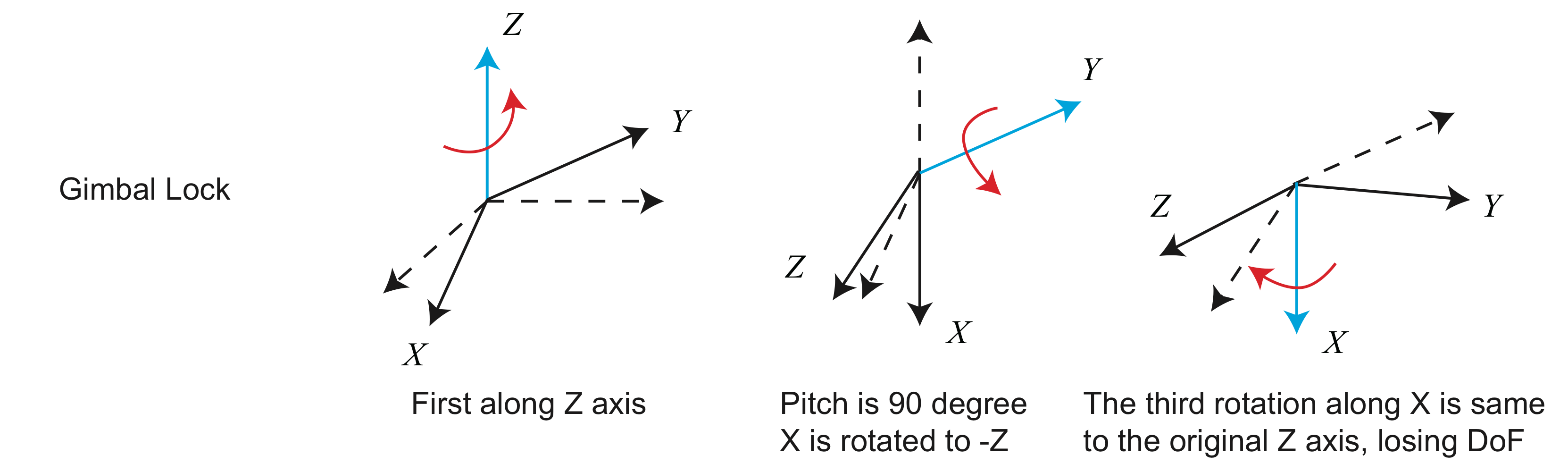
ypr의 경우, pitch가 \( \pm 90^\circ \)일 때 첫 번째 회전과 세 번째 회전이 같은 회전축을 갖게 되어 표현 가능한 회전이 3DoF에서 2DoF로 줄어들게 된다.
이는 singularity problem이라 불리며, 모든 Euler angle 형태에서 발생하는 문제이다.
따라서 Euler angle로 나타내는 것은 human-computer interaction 분야에서 많이 사용되는 interpolation이나 iteration 시에는 적절하지 않다. 즉, SLAM에서 pose를 표현할 때나 filtering 혹은 optimization 시에는 Euler angle은 잘 사용되지 않는다.
하지만 앞서 말했듯이 사람이 회전을 직관적으로 파악할 때 유리하므로, 작성한 알고리즘이 맞는지 확인할 때 회전을 Euler angle 표현으로 변환한 후에 검증해보는 등의 과정에서 많이 사용한다.
Quaternions
위에서 알아본 Rotation matrix는 redundancy의 문제, Euler angle은 singularity의 문제를 갖고있다.
Quaternion은 복소수 (complex number)를 확장한 개념이다.
좀 더 자세히 알아보면, Complex number은 수직선으로 표현되는 real number를 2차원 복소 평면으로 확장한 것이고,
Quaternion은 이러한 복소 평면을 3차원으로 확장하여 표현하는 개념이다. (3D Vision에서 매우 중요한 의미를 갖는 개념이다!)
깊게 들어가면 4차원 공간의 이해가 필요한데, 여기서는 굳이 그까지는 다루지 않고, quaternion을 어떻게 회전에서 다루는지 정도까지만 살펴볼 것이다.
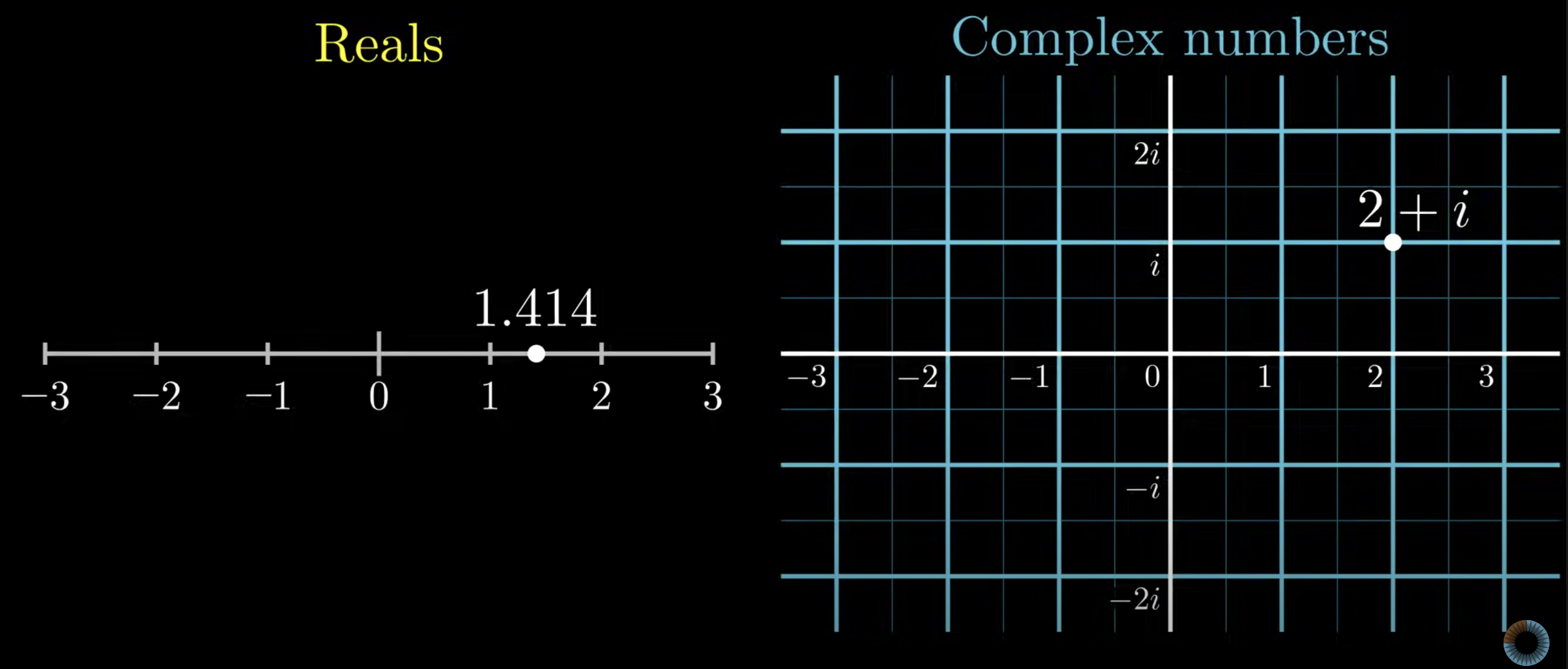
복소수를 간단히 복습해보자.
복소수는 complex set \(\mathbb{C}\)를 사용하여 2D complex plane 상의 벡터를 표현한다.
쉽게 말해, 앞서 언급했듯 모든 실수는 수직선으로 표현될 수 있는데, 거기에 (y축을 더한다는 개념으로 \(i\)축을 더하면) 한 차원을 더하여 complex number를 표현할 수 있다.
또한, 2D plane의 회전을 표현할 때 단위 복소수의 곱을 사용한다. (예를 들어, complex \(i\)를 곱하는 것은 complex vector를 반시계방향으로 90도 회전하는 것과 같다.)
이를 3차원 공간으로 확장시킨 것이 바로 Quaternion이다.
Quaternioin은 compact하면서 singularity 문제도 없다. 단점이라면 직관적이지 않고, 연산이 복잡한 정도이다.
Quaternion을 쉽게 이해하기 위해 복소수와 비교해보자.
복소평면 상의 벡터를 \(\theta\)만큼 회전시키고 싶다고 하자. 이때 해당 complex vector에 \(e^{i \theta}\)를 곱하면 된다. (polar coordinates 개념)
이는 그유명한 Euler equation으로도 표현될 수 있다.
\( e^{i \theta} = \cos \theta + i \sin \theta \)
이것은 단위길이를 갖는 복소수이다. 따라서 2차원에서의 회전은 단위 복소수로 표현된다.
이와 비슷하게, 3차원에서의 회전은 unit quaternion으로 표현된다.
Representations of Quaternion
Quaternion \(\boldsymbol{q}\)는 real part(실수부) 하나와 imaginary part(허수부) 세 개로 구성된다.
이 책에서는 real part를 앞에, imaginary part를 뒤에 써서 다음과 같이 표현한다.
\( \boldsymbol{q} = q_0 + q_1 i + q_2 j + q_3 k \)
\(i, j, k\)는 imaginary parts로, 다음을 만족한다.
\( \begin{cases} i^2 = j^2 = k^2 = ijk = -1 \\ ij = k, ji = -k \\ jk = i, kj = -i \\ ki = j, ik = -j \end{cases} \)
두 번째 줄부터 네 번째 줄은 마치 x축, y축, z축의 단위벡터(\(\hat{i}, \hat{j}, \hat{k}\))와 비슷하다는 느낌을 받는다. (두 단위벡터 간의 외적)
실제로 \(i, j, k\)를 세 개의 축으로 생각하는 개념이 이해가 편하다.
또한, scalar와 vector를 사용하여 quaternion을 표현할 수 있다.
\( \boldsymbol{q} = \left[ s, \boldsymbol{v} \right]^T, \quad s = q_0 \in \mathbb{R}, \quad \boldsymbol{v} = \left[ q_1, q_2, q_3 \right]^T \in \mathbb{R}^3 \)
\(s\)는 스칼라로, quaternion의 실수부를 나타내고, \(\boldsymbol{v}\)는 허수부를 나타내는 벡터이다.
또한 \(\boldsymbol{v} = \boldsymbol{0}\)이면 real quaternion, \(s = 0\)이면 imagninary quaternion이다.
앞서 unit quaternion을 통해 3D rotation을 표현할 수 있다고 했는데, 이러한 표현은 복소수(2D)에서와는 조금 다르다.
복소수에서는 \(i\)를 곱하는 것이 90도 회전하는 것을 의미하지만, 이 개념을 그대로 quaternion에 적용시키면 \(ij = k\)라는 수식은 마치 \(i\)기준으로 90도 돌린 후 \(j\) 기준으로 90도 돌리면 \(k\) 기준으로 90도 돌린 것과 같다는 의미가 되어버린다. (당연히 아니다. 주변에 보이는 물체 하나를 잡고 축을 설정한 후 돌려보면 금방 알 수 있다.)
대신, quaternion에서 \(i\)를 곱한다는 것은 해당 축으로 180도를 회전시킨다는 것을 의미한다. 휴대폰을 세 축을 기준으로 돌려보면 확인해볼 수 있다.
또한, \(i^2 = -1\)은 \(i\)축 기준으로 360도를 돌리면 반대 방향이 된다는 것을 말한다. 즉 720도를 돌려야 원래대로 돌아오는 것이다.
너무 깊은 내용에 머리아플 필요 없이, '3차원 공간의 회전을 Quaternion을 통해 compact하면서도 어떤 문제 없이 명확히 표현이 가능하다' 정도로 알아두자.
Quaternion Operations
더하고, 빼고, 곱하는 등의 연산은 Quaternion에 대한 완벽한 이해가 없이도 수치적으로 충분히 할 수 있다.
연산 방식은 complex number에서와 같기 때문이다.
두 quaternion '\( \boldsymbol{q}_a = s_a + x_a i + y_a j + z_a k\)', '\(\boldsymbol{q}_b = s_b + x_b i + y_b j + z_b k \)'가 있다고 하자. 또한 각각 '\( \left[ s_a, \boldsymbol{v}_a \right]^T\)', '\(\left[ s_b, \boldsymbol{v}_b \right] \)'로 나타낼 수 있다.
Addition and Subtraciton
덧셈과 뺄셈은 아주 간단히, scalar(실수부)는 scalar끼리, vector(허수부)는 vector끼리 더하면 된다.
\( \boldsymbol{q}_a \pm \boldsymbol{q}_b = \left[ s_a \pm s_b, \; \boldsymbol{v}_a \pm \boldsymbol{v}_b \right]^T \)
Multiplication
Quaternion의 곱은 \(\boldsymbol{q}_a\)의 각 항과 \(\boldsymbol{q}_b\)의 각 항의 곱으로 나타낸다.
\( \begin{align*} \boldsymbol{q}_a \boldsymbol{q}_b &= s_a s_b - x_a x_b - y_a y_b - z_a z_b \\ & + (s_a x_b + x_a s_b + y_a z_b - z_a y_b ) i \\ & + (s_a y_b - x_a z_b + y_a s_b + z_a x_b ) j \\ & + (s_a z_b + x_a y_b - y_a x_b + z_a s_b ) k \end{align*} \)
스칼라로 나타냈을 때는 매우 복잡해 보이지만, vector form은 더 간결하게 표현할 수 있다.
\( \boldsymbol{q}_a \boldsymbol{q}_b = \left[ s_a s_b - \boldsymbol{v}_a^T \boldsymbol{v}_b , \; s_a \boldsymbol{v}_b + s_b \boldsymbol{v}_a + \boldsymbol{v}_a \times \boldsymbol{v}_b \right]^T \)
이러한 결과에 따라, quaternion 곱 결과의 실수부는 여전히 실수부이고, 허수부는 여전히 허수부로 남는다는 것을 알 수 있다.
그리고 허수부의 outer product 때문에 quaternion 곱은 교환법칙이 성립하지 않는다. (\( \boldsymbol{q}_a \boldsymbol{q}_b \neq \boldsymbol{q}_b \boldsymbol{q}_a \))
만약 두 허수부 벡터가 서로 평행하다면 outer product 값이 0이므로 교환법칙이 성립한다.
Length
Quaternion의 길이 또한 Complex number에서와 비슷하다.
\( \lVert \boldsymbol{q}_a \rVert = \sqrt{s_a^2 + x_a^2 + y_a^2 + z_a^2} \)
이에 따라 두 quaternion의 product 결과의 길이는 각 길이의 prodcut와 같다는 사실을 쉽게 알 수 있다.
그러므로 unit quaternion은 다른 unit quaternion과 곱해져도 unit-length를 유지한다.
\( \lVert \boldsymbol{q}_a \boldsymbol{q}_b \rVert = \lVert \boldsymbol{q}_a \rVert \lVert \boldsymbol{q}_b \rVert \)
Conjugate
Quaternion의 conjugate(켤레)는 허수부의 부호를 반대로 하는 것과 같다. (마찬가지로 Complex Number와 동일한 개념이다.)
\( \boldsymbol{q}_a^\ast = s_a - x_a i - y_a j - z_a k = \left[ s_a, - \boldsymbol{v}_a \right]^T \)
따라서 quaternion과 그것의 켤레를 곱하면 real quaternion을 얻고, 그 real part의 길이는 제곱이 된다.
\( \boldsymbol{q}^\ast \boldsymbol{q} = \boldsymbol{q} \boldsymbol{q}^\ast = \left[ s^2 + \boldsymbol{v}^T \boldsymbol{v}, \boldsymbol{0} \right]^T \)
Inverse
Quaternion의 inverse는 다음과 같이 정의된다.
\( \boldsymbol{q}^{-1} = \boldsymbol{q}^\ast / \lVert \boldsymbol{q} \rVert^2 \)
이에 따라 quaternion과 그 inverse의 product는 real quaternion \(\boldsymbol{1}\)과 같다.
\( \boldsymbol{q} \boldsymbol{q}^{-1} = \boldsymbol{q}^{-1} \boldsymbol{q} = \boldsymbol{1} \)
또한, unit quaternion은 inverse와 conjugate가 같다. 이에 따라 두 unit quaternion의 product의 inverse는 각 inverse의 product와 같다.
\( \left( \boldsymbol{q}_a \boldsymbol{q_b} \right)^{-1} = \boldsymbol{q}_b^{-1} \boldsymbol{q}_a^{-1} \)
Scalar Multiplication
Quaternion에 scalar(실수)를 곱할 경우, 간단히 다음과 같은 결과를 보인다.
\( k \boldsymbol{q} = \left[ ks, k \boldsymbol{v} \right]^T \)
Quaternion to Represent a Rotation
이제 3D Rotation을 quaternion으로 나타내는 방법을 알아보자.
spatial 3D point \( \boldsymbol{p} = \left[ x, y, z \right]^T \in \mathbb{R}^3 \)에 대한 회전이 quaternion \( \boldsymbol{q} \)로 나타나며, 회전 결과 \( \boldsymbol{p}^\prime \)이 된다.
먼저 Quaternion을 통해 회전을 나타낼 때에는 3D point를 quaternion으로 확장해주어야 한다.
\( \boldsymbol{p} = \left[ 0, x, y, z \right]^T = \left[ 0, \boldsymbol{v} \right]^T \)
간단히 imaginary part에 세 개의 coordinate를 두고 real part는 0으로 두었다.
이때 회전 결과는 다음과 같이 quaternion의 product로 나타낸다.
\( \boldsymbol{p}^\prime = \boldsymbol{q} \boldsymbol{p} \boldsymbol{q}^{-1} \)
곱셈은 quaternion multiplication이며, 결과 또한 (pure imaginary) quaternion이다. Quaternion인 \(\boldsymbol{p}^\prime\)의 허수부가 바로 회전 후의 좌표이다.
Conversion of Quaternions to Other Rotation Representations
Quaternion을 사용한 회전을 다른 표현(특히 rotation matrix와 rotation vector)으로 바꿀 수 있다.
여기서 각각의 과정을 자세히 다루지는 않고, 결과만 살펴보자.
Quaternion \(\boldsymbol{q} = \left[ s, \boldsymbol{v} \right]^T \)에 대해
quaternion에서 rotation matrix로 바꾼 결과는 다음과 같다.
\( \boldsymbol{R} = \boldsymbol{v} \boldsymbol{v}^T + s^2 \boldsymbol{I} + 2s \boldsymbol{v}^\wedge + ( \boldsymbol{v}^\wedge )^2 \)
이러한 rotation matrix를 rotation vector로 바꾸면 다음을 얻는다.
\( \begin{cases} \theta = 2 \arccos q_0 \\ \left[ n_x, n_y, n_z \right]^T = \left[ q_1, q_2, q_3 \right]^T / \sin{\frac{\theta}{2}} \end{cases} \)
Affine and Projective Transformation
앞서 살펴본 변환은 Euclidean transformation이었다. 이는 3차원 공간에서 가능한 변환 중 가장 간단한 형태로, 벡터의 길이와 각도를 유지, 즉 rigid body의 외형을 변화시키지 않으며, transform matrix는 다음 형태를 가진다고 하였다.
\( \boldsymbol{T} = \begin{bmatrix} \boldsymbol{R} & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \)
이외에도 affine transform, projective transform 등 camera geometry와 관련된 다른 변환이 많이 존재한다. 이들 변환 또한 비슷한 similar matrix representation을 갖는데, 자세한 내용은 추후에 다루고 간단한 내용만 살펴보자.
Similarity Transformation
번역하면 '닮음 변환'으로, rigid body (object)가 균일하게 scale되는 경우를 말한다. Euclidean transformation보다 DoF가 하나 더 크며, 다음과 같은 transformation matrix 를 갖는다.
\( \boldsymbol{T}_S = \begin{bmatrix} s \boldsymbol{R} & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \)
Rotation matrix 앞에 scaling factor \(s\)가 추가되었음을 주목하자.
이로 인해 similarity transformation은 volume을 유지하지 못한다.
cube에 similarity transform을 적용하면, 부피는 바뀔 수 있어도 여전히 cube이다.
이러한 3차원 similarity transform의 집합을 similarity transform group이라 하고, \(\text{Sim} \left( 3 \right)\)로 표현한다.
Affine Transformation
Affine transformation matrix는 다음과 같다.
\( \boldsymbol{T}_A = \begin{bmatrix} \boldsymbol{A} & \boldsymbol{t} \\ \boldsymbol{0}^T & 1 \end{bmatrix} \)
여기서는 rotation matrix \(\boldsymbol{R}\) 대신에 \(\boldsymbol{A}\)로 아예 바뀌었다. \(\boldsymbol{A}\)는 더 이상 orthogonal matrix일 필요가 없으며, invertible 조건만 만족하면 된다.
이에 따라 affine transformation은 orthogonal projection이라고도 하며, cube에 적용될 시 정사각형이었던 면이 평행사변형이 된다.
Perspective Transformation
Perspective transform은 가장 일반적인 변환이다. 변환 행렬은 다음과 같다.
\( \boldsymbol{T}_P = \begin{bmatrix} \boldsymbol{A} & \boldsymbol{t} \\ \boldsymbol{a}^T & v \end{bmatrix} \)
여기서는 왼쪽 위 corner 부분이 invertable matrix \(\boldsymbol{A}\), 왼쪽 아래 corner에 scale을 나타내는 vector \(\boldsymbol{a}^T\), 오른쪽 아래에 scalar \(v\)가 사용되었다.
\(v \neq 0\)이라면 행렬 전체를 \(v\)로 나누어 오른쪽 아래 값을 1로 만들어줄 수 있다.
하지만 \(v = 0\)이면 2D perspective transformation은 8 DoF, 3D perspective transformation은 15 DoF를 갖게 된다. (3 × 3 행렬에서 오른쪽 아래 값 하나, 4 × 4 행렬에서 오른쪽 아래 값 하나만 0이므로!)
이러한 perspective transformation은 real world에서 camera photo로의 변환을 나타낸다.
예를 들어, 실제 세계에서의 정사각형은 사진에서 (원근법의 영향으로) 직사각형도, 평행사변형도 아닌 사다리꼴 모양을 띄게 될 것이다.
여러 변환을 표로 정리하면 다음과 같다.
추후에 각각에 대해 좀 더 자세히 다뤄볼 것이다.
최근댓글