PyTorch를 간단히 다루어본 적이 있는데, 앞으로의 연구에 익숙하게 활용하기 위해 PyTorch 내용을 정리해보려 한다.
대부분의 내용은 유튜브의 '모두를 위한 딥러닝 시즌2'를 참고하였다.
기본적인 딥러닝 내용과 파이썬 문법은 어느 정도 알고 있다고 가정하고, PyTorch 실습 내용 위주로 정리해두었다.
https://www.youtube.com/watch?v=1Lp9LW6nObg&list=PLQ28Nx3M4JrhkqBVIXg-i5_CVVoS1UzAv&index=16
간단한 설명이 포함된 실습 자료는 Github를 참조하자.
GitHub - JJukE/Pytorch_DL_for_everyone: 파이토치 익히기 위해 '모두를 위한 딥러닝' 수강
파이토치 익히기 위해 '모두를 위한 딥러닝' 수강. Contribute to JJukE/Pytorch_DL_for_everyone development by creating an account on GitHub.
github.com
목차
1. Overfitting
머신러닝에서 모델을 학습시킬 때, 우리는 학습용 데이터와 테스트용 데이터를 따로 사용한다.
학습용 데이터를 얼마나 학습했는가에 따라 다음 그림과 같이 분류할 수 있다.
위 그림에서 Underfitting은 모델이 아직 학습이 덜 된 것이고, Overfitting은 학습용 데이터에 너무 과적합된 상태이다.
모델을 학습시킨 궁극적인 목적은 한번도 보지 않은 데이터(unseen data)를 얼마나 잘 예측하는가, 즉 일반화(generalization)를 얼마나 잘 하는가인데, Overfitting된 모델의 경우에는 학습용 데이터는 아주 잘 설명할 수 있으나, 새로운 데이터를 제대로 설명할 수 없게 된다.
1) Overfitting 해결 방법
이러한 Overfitting을 해결하는 방법은 여러가지가 있다.
- training data의 양을 늘린다.
- feature의 수를 줄인다.
- Regularization기법을 사용한다.
- Dropout을 적용한다.
이 중에서도, Dropout에 대해 알아보자.
2) Dropout
Dropout은 위 그림에서와 같이, 각 Layer의 모든 노드를 연결시키는 대신에, 무작위로 몇몇 연결을 끊는(노드를 사용하지 않는) 것이다.
위 예시의 경우, 각 Layer에서 5개 중 3개의 노드만 사용한 것이다.
애초에 노드를 적게 사용하면 되지 않냐고 생각할 수 있는데, Dropout의 경우에는 각 train data에 따라 (같은 개수의)서로 다른 노드들을 사용하게 된다.
따라서, 매번 조금씩 다른 네트워크를 사용하여 학습하게 되는, network ensemble의 효과를 얻을 수 있게 됨으로써 일반화 성능을 높이게 된다.
3) Dropout Implementation
실습을 해보자.
Dropout은 다음과 같이 사용한다.
# nn Layers
linear1 = torch.nn.Linear(784, 512, bias=True)
linear2 = torch.nn.Linear(512, 10, bias=True)
relu = torch.nn.ReLU()
dropout = torch.nn.Dropout(p=drop_prob)
# model
model = torch.nn.Sequential(linear1, relu, dropout,
linear2)
단, Dropout을 사용할 때 주의할 점이 있다.
Dropout은 Train 시에는 사용하지만, Test 시에는 학습된 모든 노드를 사용해야 한다. 즉, Test 시에는 Dropout을 적용하지 않아야 한다.
따라서, 다음과 같이 Train mode, eval mode를 나누어준다.
...
total_batch = len(data_loader)
model.train() # set the model to train mode (dropout=True)
for epoch in range(training_epochs):
...
...
# Test model and check accuracy
with torch.no_grad():
model.eval() # set the model to evaluation mode (dropout=False)
...
여기서 model.train() 함수와 model.eval()함수는 모듈을 training 또는 evaluation mode로 만들어 주고, Dropout, Batch Normalization 등을 적용할 때 사용된다.
전체 코드는 Batch Normalization까지 알아본 후에 작성해보자.
2. Batch Normalization
Batch Normalization은 Backpropagation 과정에서의 Gradient Vanishing과 Exploding 문제를 해결해주며, 추가로 학습을 안정적으로 진행되도록 해준다.
1) Gradient Vanishing / Exploding
Gadient Vanishing Problem의 경우, Sigmoid Function의 문제점을 설명할 때 언급했던 부분이다.
간단히 다시 설명하자면, backpropagtion에서 에러(loss)가 전파될 때 gradient와 곱해지게 되는데, sigmoid function의 개형을 보면 양쪽 끝 부분에서 기울기가 거의 0에 가까워지면서, 전파되는 값이 0에 수렴해버리는 문제이다.
Gradient Exploding의 경우 반대로 gradient가 너무 커서 전파되는 값이 발산하는 문제이다.
이러한 Gradient Vanishing과 Exploding 문제를 해결하는 방법은 아래와 같다.
- Activation Function을 바꾼다.
- 적절한 Weight Initialization 방법을 적용한다.
- Learning Rate를 작게 설정한다.
- Batch Normalization을 적용한다.
2) Internal Covariate Shift
Internal Covariate Shift는 위에서 언급한 Gradient Vanishing 및 Exploding을 유발하는 원인이다.
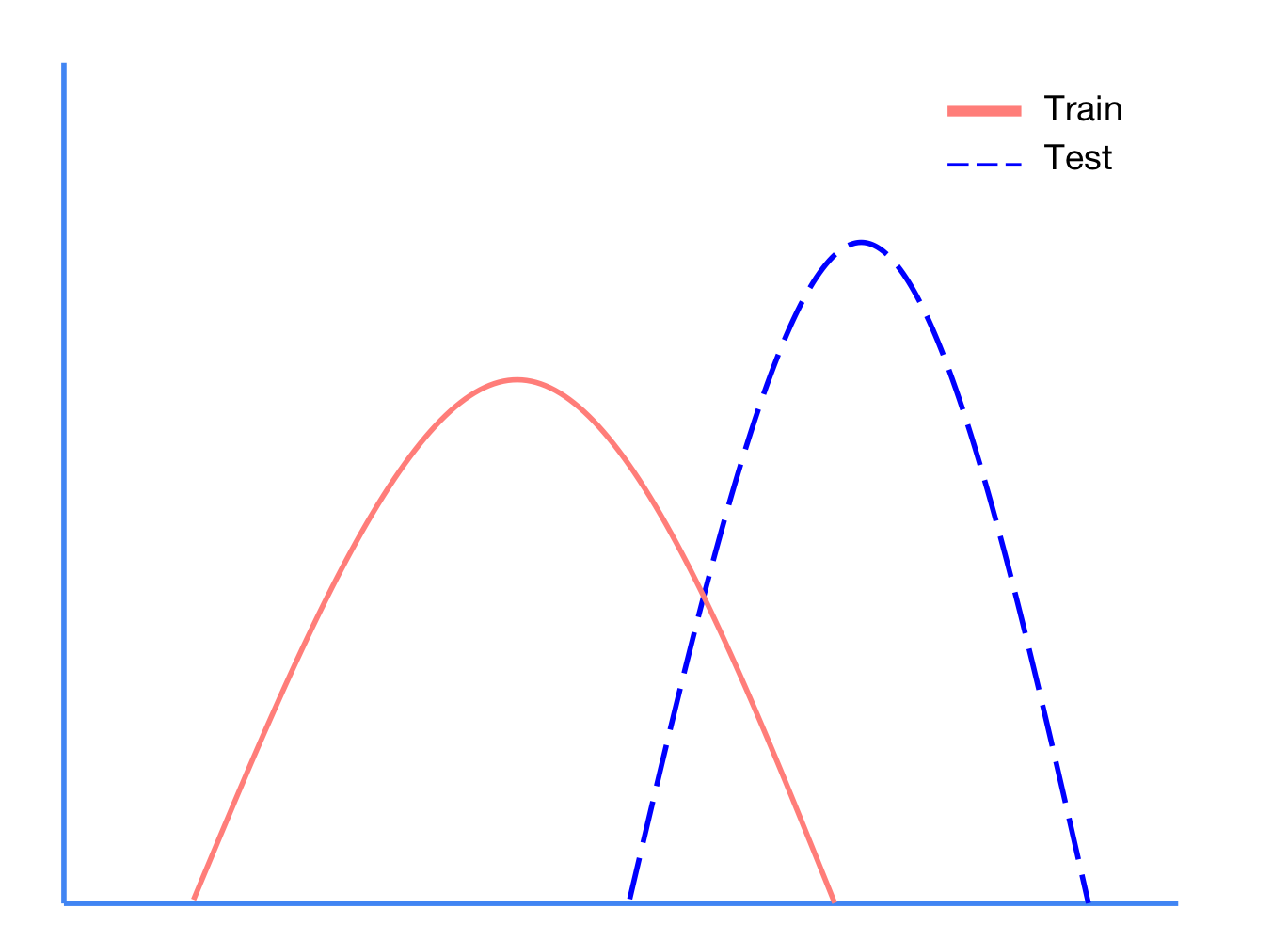
Covariate Shift란, train dataset과 test dataset이 위와 같이 다른 분포를 갖게 될때 일어나는 문제점이다.
다음과 같이 고양이 사진을 보고 고양이라고 예측하는 모델을 학습시킨다고 가정하자.
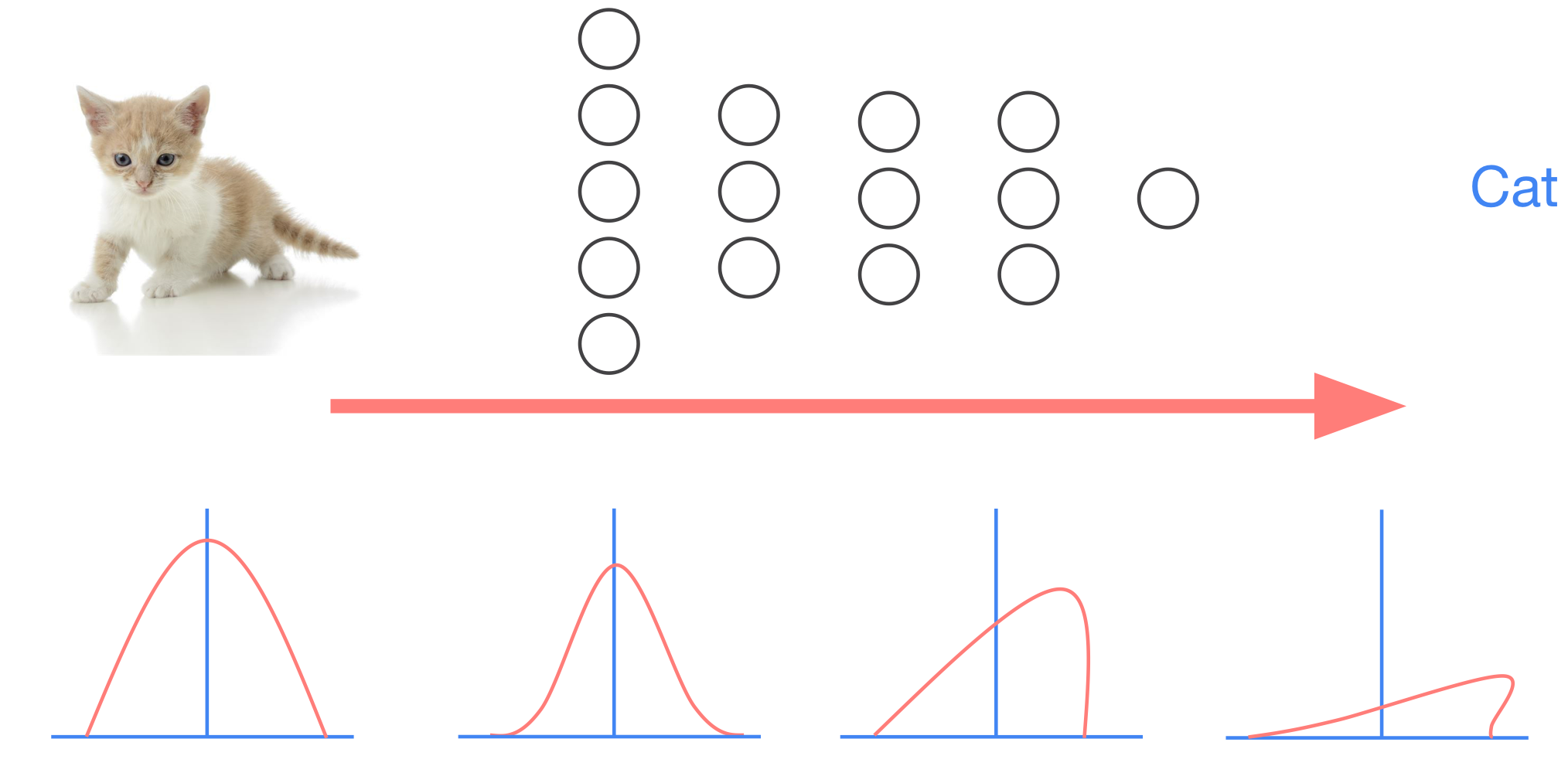
train dataset은 애초에 가장 왼쪽의 분포를 갖고 있다고 가정하자.
학습의 과정에서 forward pass, backward pass를 지나면서 layer를 거칠 때마다 covariate shift가 일어나 점점 분포가 변하게 된다.
Batch Normalization은 이러한 Internal Covariate Shift 문제를 직접적으로 해결해준다.
3) Batch Normalization
Batch Normalization은 Input으로 mini-batch \( \mathcal{B} = \{x_1, ... , x_m \} \) 내의 \(x\)의 값을 받고, output으로 parameters \(\gamma, \beta\)에 대한 \( y_i = \text{BN}_{\gamma, \beta} (x_i) \)를 내며, 다음 수식을 따라 이루어진다.
[mini-batch mean] - mini batch의 평균
\( \mu_\mathcal{B} \leftarrow \frac{1}{m} \overset{m}{\underset{i=1}{\sum x_i}} \)
[mini-batch variance] - mini batch의 분산
\( \sigma^2_\mathcal{B} \leftarrow \frac{1}{m} \overset{m}{\underset{i=1}{\sum (x_i - \mu_\mathcal{B})^2}} \)
[normalize] - 정규화 (\(\epsilon\): 매우 작은 값)
\( \hat{x}_i \leftarrow \frac{x_i - \mu_\mathcal{B}}{\sqrt{\sigma^2_\mathcal{B} + \epsilon}} \)
[scale and shift] - transform
\( y_i \leftarrow \gamma \hat{x}_i + \beta \equiv \text{BN}_{\gamma, \beta} (x_i) \)
parameter \(\gamma, \beta\)는 batch normalization을 계속 진행하면서 activation function의 non-linearity 성질을 잃게 되는 현상을 완화시켜주기 위한 것으로, weight, bias와 마찬가지로 모델이 학습하는 파라미터이다.
4) Batch Normalization Implementation
BN 실습을 해보자. 다음과 같은 함수를 사용한다.
## nn layers
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.Linear(32, 10, bias=True)
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)
# model
bn_model = torch.nn.Sequential(linear1, bn1, relu,
linear2)
3. Whole Implementation
Batch Normalization 적용 모델, Dropout적용 모델, 일반 neural network 모델을 각각 따로 만들어 세 가지 모델을 비교해보는 실습을 해보자.
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pylab as plt
# parameters
learning_rate = 0.01
training_epochs = 10
batch_size = 32
drop_prob = 0.3
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)
# dataset loader
train_loader = torch.utils.data.DataLoader(dataset=mnist_train,
batch_size=batch_size,
shuffle=True,
drop_last=True)
test_loader = torch.utils.data.DataLoader(dataset=mnist_test,
batch_size=batch_size,
shuffle=False,
drop_last=True)
# nn layers
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 32, bias=True)
linear3 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.ReLU()
dropout = torch.nn.Dropout(p=0.3)
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)
nn_linear1 = torch.nn.Linear(784, 32, bias=True)
nn_linear2 = torch.nn.Linear(32, 32, bias=True)
nn_linear3 = torch.nn.Linear(32, 10, bias=True)
# model
bn_model = torch.nn.Sequential(linear1, bn1, relu,
linear2, bn2, relu,
linear3)
do_model = torch.nn.Sequential(linear1, relu, dropout,
linear2, relu, dropout,
linear3)
nn_model = torch.nn.Sequential(nn_linear1, relu,
nn_linear2, relu,
nn_linear3)
# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss() # Softmax is internally computed.
bn_optimizer = torch.optim.Adam(bn_model.parameters(), lr=learning_rate)
do_optimizer = torch.optim.Adam(do_model.parameters(), lr=learning_rate)
nn_optimizer = torch.optim.Adam(nn_model.parameters(), lr=learning_rate)
# Save Losses and Accuracies every epoch
# We are going to plot them later
train_losses = []
train_accs = []
valid_losses = []
valid_accs = []
train_total_batch = len(train_loader)
test_total_batch = len(test_loader)
for epoch in range(training_epochs):
bn_model.train() # set the model to train mode
do_model.train()
for X, Y in train_loader:
# reshape input image into [batch_size by 784]
# label is not one-hot encoded
X = X.view(-1, 28 * 28)
Y = Y
bn_optimizer.zero_grad()
bn_prediction = bn_model(X)
bn_loss = criterion(bn_prediction, Y)
bn_loss.backward()
bn_optimizer.step()
do_optimizer.zero_grad()
do_prediction = do_model(X)
do_loss = criterion(do_prediction, Y)
do_loss.backward()
do_optimizer.step()
nn_optimizer.zero_grad()
nn_prediction = nn_model(X)
nn_loss = criterion(nn_prediction, Y)
nn_loss.backward()
nn_optimizer.step()
with torch.no_grad():
bn_model.eval() # set the model to evaluation mode
do_model.eval()
# Test the model using train sets
bn_loss, do_loss, nn_loss, bn_acc, do_acc, nn_acc = 0, 0, 0, 0, 0, 0
for i, (X, Y) in enumerate(train_loader):
X = X.view(-1, 28 * 28)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
do_prediction = do_model(X)
do_correct_prediction = torch.argmax(do_prediction, 1) == Y
do_loss += criterion(do_prediction, Y)
do_acc += do_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, do_loss, nn_loss, bn_acc, do_acc, nn_acc = (bn_loss / train_total_batch, do_loss / train_total_batch,
nn_loss / train_total_batch, bn_acc / train_total_batch, do_acc / train_total_batch, nn_acc / train_total_batch)
# Save train losses/acc
train_losses.append([bn_loss, do_loss, nn_loss])
train_accs.append([bn_acc, do_acc, nn_acc])
print(
'[Epoch %d-TRAIN] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs Dropout Loss(Acc): do_loss:%.5f(do_acc:%.2f) vs Simple NN Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), do_loss.item(), do_acc.item(), nn_loss.item(), nn_acc.item()))
# Test the model using test sets
bn_loss, do_loss, nn_loss, bn_acc, do_acc, nn_acc = 0, 0, 0, 0, 0, 0
for i, (X, Y) in enumerate(test_loader):
X = X.view(-1, 28 * 28)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
do_prediction = do_model(X)
do_correct_prediction = torch.argmax(do_prediction, 1) == Y
do_loss += criterion(do_prediction, Y)
do_acc += do_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, do_loss, nn_loss, bn_acc, do_acc, nn_acc = (bn_loss / test_total_batch, do_loss / test_total_batch,
nn_loss / test_total_batch, bn_acc / test_total_batch, do_acc / test_total_batch, nn_acc / test_total_batch)
# Save valid losses/acc
valid_losses.append([bn_loss, do_loss, nn_loss])
valid_accs.append([bn_acc, do_acc, nn_acc])
print(
'[Epoch %d-VALID] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs Dropout Loss(Acc): do_loss:%.5f(do_acc:%.2f) vs Simple NN Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), do_loss.item(), do_acc.item(), nn_loss.item(), nn_acc.item()))
print()
print('Learning finished')
# function to plot 3 models
def plot_compare(loss_list: list, ylim=None, title=None) -> None:
bn = [i[0] for i in loss_list]
do = [i[1] for i in loss_list]
nn = [i[2] for i in loss_list]
plt.figure(figsize=(9, 6))
plt.plot(bn, label='With BN')
plt.plot(do, label='With Dropout')
plt.plot(nn, label='Without BN and DO')
if ylim:
plt.ylim(ylim)
if title:
plt.title(title)
plt.legend()
plt.grid('on')
plt.show()
plot_compare(train_losses, title='Training Loss at Epoch')
plot_compare(train_accs, [0, 1.0], title='Training Acc at Epoch')
plot_compare(valid_losses, title='Validation Loss at Epoch')
plot_compare(valid_accs, [0, 1.0], title='Validation Acc at Epoch')
모든 코드를 실행한 결과는 아래와 같다.
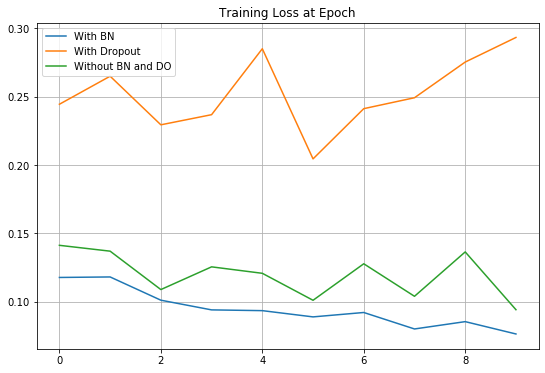
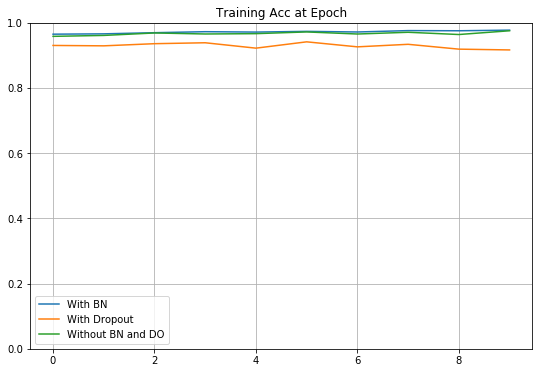
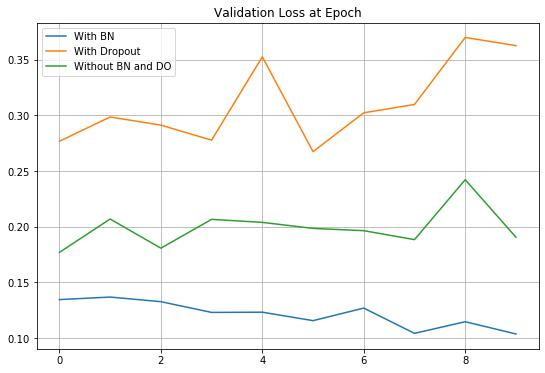
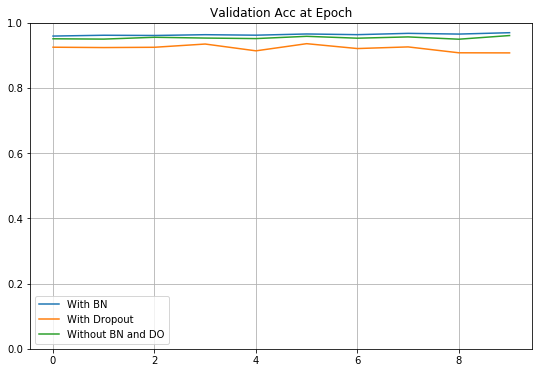
결과를 보면, 예상과 달리 Dropout을 적용한 결과가 성능이 가장 낮음을 알 수 있다.
잘 생각해보면, 층이 3개밖에 없는 간단한 모델이기 때문에 노드 간 연결을 끊는 Dropout을 적용할 경우 성능이 떨어지는 것은 당연하다.
나중에 기회가 된다면 깊은 층에 대해서도 한 번 비교를 해보고 싶다.
최근댓글