목차
이전 포스팅에서 생성모델의 개요와 이해를 위한 기초 지식까지 알아보았다.
이번 포스팅에서는 머신러닝 모델의 두 가지 종류인 Naive Bayes classifier로 대표되는 generative model의 접근방법과 Logistic regression으로 대표되는 discriminative model의 접근방법을 자세히 비교해보자.
이전에 언급했듯, classification task에서 두 모델의 목적은 데이터 \(x\)와 class label \(y\)에 대해 posterior \(p(y|x)\)를 예측한다는 공통적인 목적을 갖고 있으나, 그 접근 방법이 다르다.
Bayes Network
우선 상대적으로 익숙한 logistic regression은 제쳐두고, bayes network에 대해 알아보자.
Bayesian Network
Bayesian network에서는 chain rule과, (Markov property에 의한)conditional independence를 적용하여 compact한 representation을 얻는다. Chain rule, Bayes rule, conditional independence 등의 개념과 생성 모델에서의 활용은 이전 포스팅을 참고하자. 이 과정을 (계산량이 너무 큰 joint parameterization 대신) conditional parameterization이라 한다.
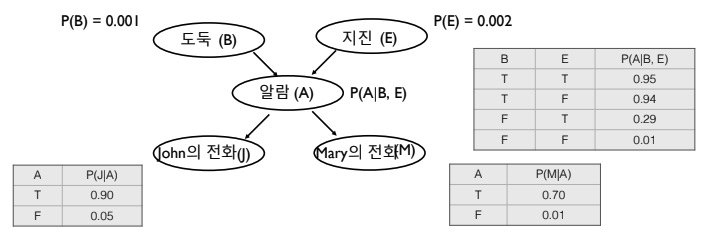
쉽게 말해, Fig 1과 같이 복잡한 모델인 결합 분포를 쉽게 표현하기 위해서 그래프(Directed Ascyclig Graph, DAG)로 표현하는데, 서로 관계가 없는 노드는 조건부 독립임을 활용하여 (소거해서) 간단히 표현해준다.
각 random variable \(x_i\)에 대해 random variable set \(\mathbf{x}_{\mathbf{A}_i}\)에 대한 distribution p(x_i \vert \mathbf{x}_{\mathbf{A}_i})를 정한다.
우선은 joint parameterization을 통해 \(p(x_1, \cdots, x_n) = \prod\limits_{i} p(x_i \vert \mathbf{x}_{\mathbf{A}_i})\)를 얻는다.
이후 chain rule으로 factorize하고, 각 factor들에 대해 conditional independence 가정(관계 없는 노드는 조건부 독립!)을 적용하여 간단한 형태를 얻는다.
특히 Bayesian network는 아래의 조건을 만족하는 directed acyclig graph \(G = (V, E)\)로 정해진다.
- 각 node \(i \in V\)의 random variable : \(x_i\)
- 각 node \(i\)의 conditional probability distribution (CPD) : \(p(x_i \vert \mathbf{x}_{\text{Pa}(i)})\)
- Parent(\(\text{Pa}\))의 node 값에 따라 conditional independent 성질을 갖게 됨
이에 따라, Bayesian network의 joint distribution은 다음과 같이 정의한다.
\( p(x_1, \cdots, x_n) = \prod\limits_{i \in V} p(x_i \vert \mathbf{x}_{\text{Pa}(i)}) \)
Example
예를 들어, 다음과 같은 DAG로 나타난 Bayesian model이 있다고 해보자.
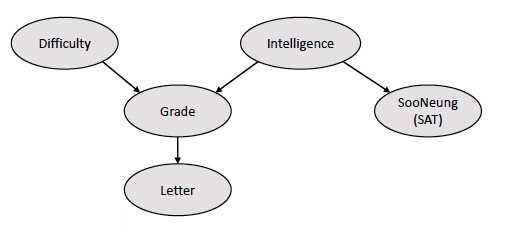
이 모델의 joint distribution을 구해보자.
우선, 단순히 모든 relation을 고려할 경우(연결? or not?)에는 distribution을 정하기 위해 \(2^5 - 1\)개의 parameter가 필요할 것이다. 하지만, Bayesian network의 정의(conditional independent 성질)를 활용하여 그 개수를 줄여줄 수 있다.
우선 각 node를 (부모노드 순으로)D, I, G, S, L이라 하자. 이때 joint distribution은 정의를 활용하여 다음과 같이 나타낼 수 있다.
\( \begin{align*} & p(D, I, G, S, L) \\ &= p(D \vert \cancel{I}, \cancel{G}, \cancel{S}, \cancel{L}) p(I \vert \cancel{D}, \cancel{G}, \cancel{S}, \cancel{L}) p(G \vert D, I, \cancel{S}, \cancel{L}) p(S \vert \cancel{D}, I, \cancel{G}, \cancel{L}) p(L \vert \cancel{D}, \cancel{I} , G, \cancel{S}) \\ &= p(D) p(I) p(G \vert I, D) p(S \vert I) p(L \vert G) \end{align*} \)
이전처럼 joint distribution에 chain rule을 적용한다고 해보자.
\(p(D, I, G, S, L) = p(D) p(I | D) p( G | I, D) p(S | G, I, D) p(L | S, G, I, D)\)
역으로 Bayesian network 정의에 의한 식과 chain rule을 적용한 식을 비교해보면, 다음과 같은 conditional independency가 있음을 유추해볼 수 있다.
\( D \bot I, \; S \bot \{ D, G \} \vert I, \; L \bot \{D, I, S\} \vert G\)
이는 곧 Fig 2에서의 그림에서 '관계 없는 노드와는 조건부 독립'임을 만족한다.
Generative Approach vs Discriminative Approach
본격적으로 스팸 메일 구분 예시를 통해 Generative approach(Naive Bayes classifier)와 Discriminative approach(Logistic regression)를 비교해보자.
\(X_i\)는 특정 단어(word), \(X\)는 단어 집합(vocabulary), email이 스팸이면 \(Y=1\), 스팸이 아니면 \(Y=0\)이라 하자. \(i\)번째 word가 등장하면 \(X_i = 1\), 아니면 \(X_i = 0\)이다.
Chain rule을 사용하면 아래와 같이 나타낼 수 있다.
\(p(Y, \mathbf{X}) = p(\mathbf{X} | Y) p(Y) = p(Y | \mathbf{X}) p(\mathbf{X}) \)
이를 Bayesian network(Directed Acyclic Graph)로 나타내면 다음과 같다.
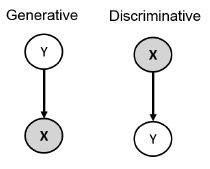
최종 목적인 prediction을 위해서는 \(p(Y|\mathbf{X})\)가 필요하다.
Generative model은 \(p(Y)\)와 \(p(\mathbf{X} | Y)\)를 둘 다 정의하고 학습한 후 Bayes rule을 통해 \(p(Y | \mathbf{X})\)를 계산해야 하지만, discriminative model은 conditional distribution \(p(Y | \mathbf{X})\)를 추정하기만 하면 된다. (p(\mathbf{X})\)는 주어졌으므로 모델링하거나, 학습하거나 사용할 필요가 없기 때문이다.
따라서 \(\mathbf{X}\)가 주어졌을 때 \(Y\)의 label을 구분하는 것만으로 따졌을 때에는 (말그대로) discriminative model이 훨씬 유용하다고 볼 수 있다.
조금 더 자세히 살펴보자.
\(\mathbf{X}\)가 random vector이므로, chain rule을 사용하면 두 모델을 다음 그림과 식으로 나타낼 수 있다.
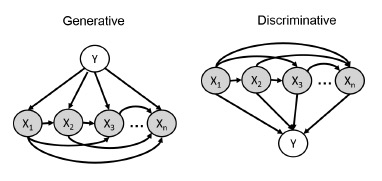
\( p(Y, \mathbf{X}) = p(Y) p(X_1 | Y) p(X_2 | Y, X_1) \cdots p(X_n | Y, X_1, \cdots, X_{n-1}) \)
\( p(Y, \mathbf{X}) = p(X_1) p(X_2 | X_1) p(X_3 | X_1, X_2) \cdots p(Y | X_1, \cdots, X_n) \)
여기서 두 가지 선택지가 존재한다.
- Generative model : \(p(Y)\)는 심플하지만, \(p(X_i | X_{\text{pa}(i)}, Y)\) term들을 어떻게 parameterize할 것인가?
- Discriminative model : \(p(Y | \mathbf{X})\)를 어떻게 parameterize할 것인가?
Generative Model (Naive Bayes Classifier)
Naive Bayes classifier에서는 모든 데이터가 조건부 독립이라고 가정하면서 식을 단순화한다. (가정 : \(X_i \bot \mathbf{X}_{1:i-1} | Y\) )
따라서 다음과 같이 나타낼 수 있다.
\( p(y, x_1, \cdots, x_n) = p(y) \prod\limits_{i=1}^n p(x_i | y) \)
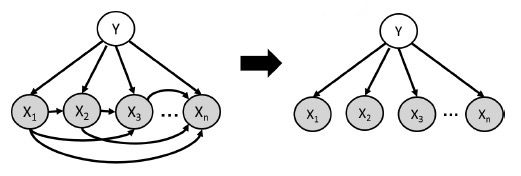
따라서 training data로부터 parameter를 추정할 수 있고, Bayes rule로 다음과 같이 prediction도 가능해진다.
\( p(Y=1 | \mathbf{X}) = \cfrac{p(Y=1, \mathbf{X})}{P(\mathbf{X})} = \cfrac{p(Y=1) \prod_{i=1}^n p(x_i | Y=1)}{\sum_{y=\{0,1\}} p(Y=y) \prod_{i=1}^n p(x_i | Y=y)} \)
참고로 분모는 discrete marginal distribution \(p(\mathbf{X})\)를 나타낸다.
Discriminative Model (Logistic Regression)
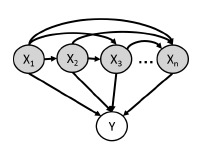
Logistic regression에서는 다음과 같이 \(\boldsymbol{\alpha}\)로 parameterize된 \(\mathbf{x}\)에 대한 function을 가정한다.
\( p(Y = 1 | \mathbf{x}; \boldsymbol{\alpha}) = f(\mathbf{x}, \boldsymbol{\alpha}) \)
- Output 값은 0에서 1 사이여야 한다. (sigmoid activation function 등 사용)
- n+1개(weight n개, bias 1개)의 parameter vector \(\boldsymbol{\alpha}\)로 함수를 표현할 수 있다. (compact representation)
대표적으로 linear dependence \(z(\boldsymbol{\alpha}, \mathbf{x}) = \alpha_0 + \sum\limits_{i=1}^n \alpha_i x_i\)와 logistic function \(\sigma(z) = 1 / (1 + \operatorname{exp}^{-z})\)로 함수 \(f\)를 다음과 같이 나타낸다.
\( p( Y = 1 | \mathbf{x}; \boldsymbol{\alpha}) = \sigma(z(\boldsymbol{\alpha}, \mathbf{x}))\)
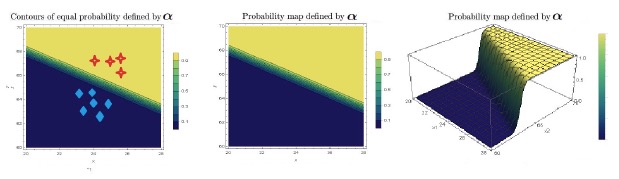
Fig 7 예시와 같이, discriminative classifier의 경우 decision boundary(예를 들어 \(p(Y=1 | \mathbf{x}; \boldsymbol{\alpha}) > 0.5\) )가 선형적이다. 즉, 서로 같은 probability의 경계선이 선형으로 나타난다. 또한, 세 번째 그림을 보면 probability의 변화가 매우 급격하게, 확실하게 나타난다.
Analysis
Logistic model은 Naive Bayes model과 달리 학습 데이터 간의 독립과 관련된 가정이 없으므로, 데이터가 많아질수록 더 정확해진다. 하지만 \(\mathbf{X}\)가 온전히 주어졌을 때에만 사용할 수 있고, misclassification 문제가 존재한다.
이에 반해, generative model의 경우 몇몇 \(x_i\) 변수가 missing(unobserved)되었을 때에도 unseen variable들을 무시(marginalize)하면서 \(p(Y | \mathbf{X}_\text{evidence})\)로 계산할 수 있게 해준다.
Neural Models
Neural model은 logistic model의 upgrade 버전으로 볼 수 있다.
Discriminative model(logistic model)에서 \(p(Y=1 | \mathbf{x}; \boldsymbol{\alpha}) = f(\mathbf{x}, \boldsymbol{\alpha})\)라 하고, linear dependence를 적용했는데, neural model에서는 non-linear dependence를 적용한다.
\(\mathbf{h}(A, \mathbf{b}, \mathbf{x}) = f(A \mathbf{x} + \mathbf{b}) \quad \text{where } \mathbf{h} \text{ is a non-linear function} \)
즉, 아래와 같이 pdf(probability density function)를 parameterize하는 개념이다.
\( p_\text{neural} (Y=1 | \mathbf{x}; \boldsymbol{\alpha}, A, \mathbf{b}) = \sigma (\alpha_0 + \sum_{i=1}^n \alpha_i h_i ) \)
- More flexible
- More parameters \(A, \mathbf{b}, \boldsymbol{\alpha}\)
이러한 함수가 여러 번 반복되면 바로 neural network가 되는 것이다.
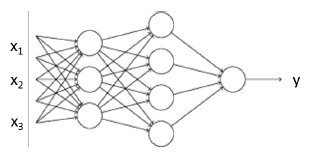
Bayesian network과 비교해보자면, "chain rule을 사용한 모델(fully general) → Bayes network(conditional independency) → Neural model(functional form으로 joint distribution을 근사)"로 이해해볼 수 있다.
- Using chain rule
- \(p(x_1, x_2, x_3, x_4) = p(x_1) p(x_2 | x_1) p(x_3 | x_1, x_2) p(x_4 | x_1, x_2, x_3) \)
- Bayes network
- \( p(x_1, x_2, x_3, x_4) = p(x_1) p(x_2 | x_1) p(x_3 | \cancel{x_1}, x_2) p(x_4 | x_1, \cancel{x_2}, \cancel{x_3}) \)
- Neural model
- \( p(x_1, x_2, x_3, x_4) \approx p(x_1) p(x_2 | x_1) p_\text{neural} (x_3 | x_1, x_2) p_\text{neural} (x_4 | x_1, x_2, x_3) \)








최근댓글