목차
이전 포스팅에서 3차원 공간에 존재하는 물체의 shape을 표현하는 다양한 방법을 알아보았다. 이번에는 shape generation 등의 3D Vision task에서 이러한 representation을 학습하는 다양한 방법, 대표적인 모델을 간단히 알아보자.
Generative Adversarial Networks (GAN)
GAN은 discriminator, generator를 경쟁적으로 training하여 target data의 embedding을 학습시킨다. Generator는 discriminator를 속여 진짜같은 이미지를 만들어내고, discriminator는 진짜 이미지와 generator가 생성한 이미지 중 무엇이 진짜인지를 구별한다.
GAN을 여러 방법으로 보완한 Deep conv GAN, Conditional Adversarial Network 등이 존재한다.
GAN에서 사용한 loss function 등 좀 더 자세한 내용은 링크를 참조하자.
3D 도메인에서는 GAN으로 voxel 형태의 object를 생성하거나, parameterization plane들을 활용하여 topological sphere shape을 생성한다.
하지만 가장 큰 문제점은 GAN 모델의 학습은 unstable하다는 점이다.
Auto-encoder based Models
Auto-encoder는 encoder와 decoder로 구성되는 모델로, 이를 기반으로 한 다양한 모델들이 representation 학습에 자주 사용된다.
(Variational) Auto-Encoder
먼저, auto-encoder(AE)와 variational auto-encoder(VAE)의 차이를 알아보자.
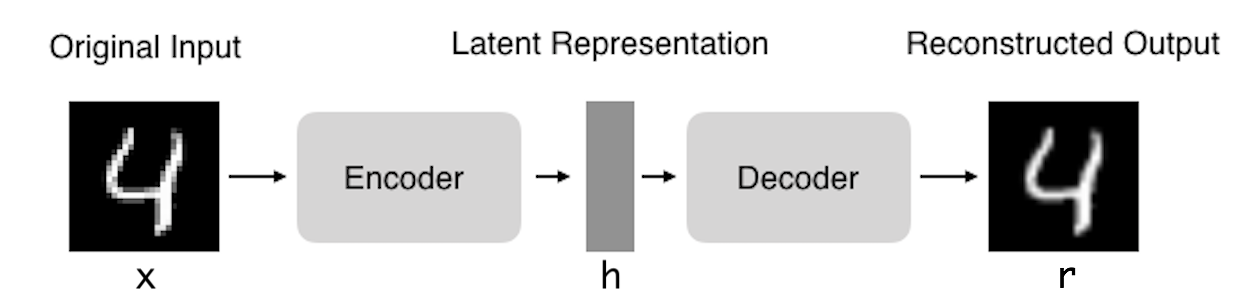
- Encoder : Input data의 feature를 뽑는다.
- Decoder : Feature로부터 input과 비슷한 data를 복원(reconstruction)한다.
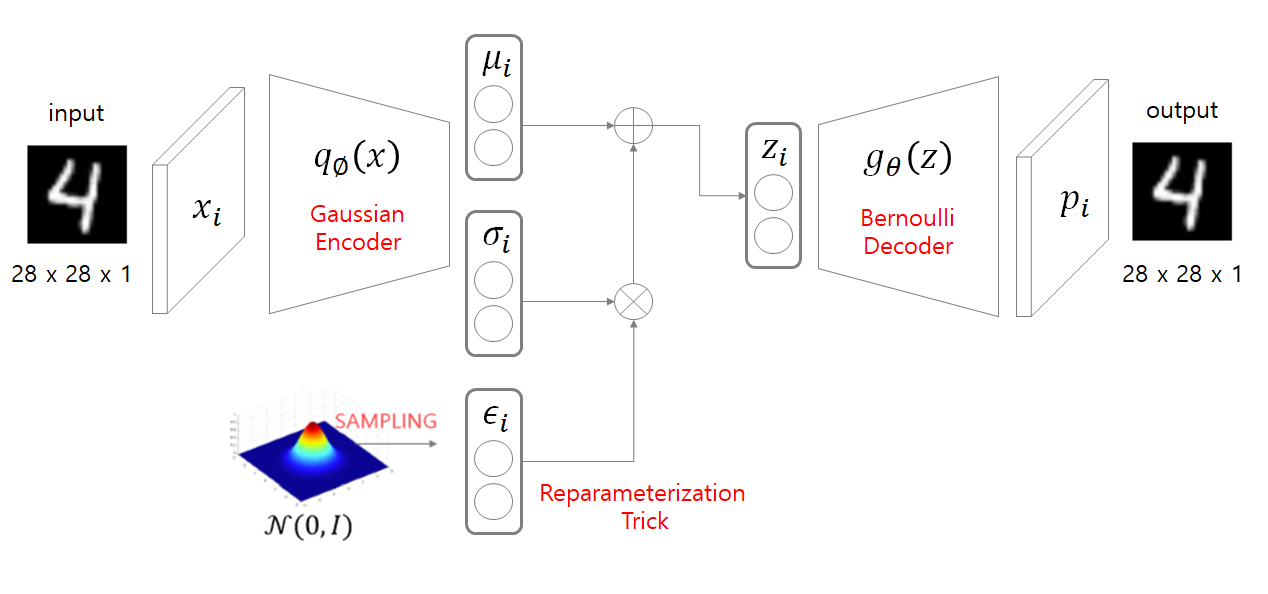
- Encoder : Input data의 latent variable의 모수(parameter), 즉 mean, variance를 구한다.
- Reparameterization Trick : Encoder의 결과를 바로 decoder에 입력하면 AE와 같이 input에 대해 하나의 output만 나올 것이다. (Reconstruction) 하지만 VAE는 generative model로, data의 분포에서 하나를 뽑아 새로운 data를 생성하는 역할을 수행한다. 따라서 encoder에서 얻은 분포에서 sampling을 진행해야 하는데, 단순히 sampling하면 backpropagation을 할 수 없으므로, reparameterization trick을 사용한다.
- 단순 sampling : \( z^{i,l} \sim \mathcal{N}(\mu_i, \sigma_i^2 \mathbf{I}) \)
- Reparameterization trick : \( z^{i,l} = \mu_i + \sigma_i^2 \odot \epsilon, \quad \text{where } \epsilon \sim \mathcal{N}(0, \mathbf{I}) \)
- 같은 distrbution이지만 reparameterization trick을 사용할 경우 backpropagation 가능
- Decoder : 샘플링한 latent variable에서 새로운 image 생성
좀 더 자세한 내용은 링크를 참조하자.
(Variational) auto-encoder로 representation을 학습하는 다양한 모델이 있다. 실제로 3D shape learning에서도 auto-encoder를 활용한 다양한 모델이 있는데, 대표적인 예로 3d-encoder-predictor CNN, Compositional VAE, AtlasNet, DeepSDF가 이에 해당한다. (엄밀히 말하자면 DeepSDF는 auto-encoder가 아닌 auto-decoder이기는 하다.)
Vector Quantized Variational Auto-Encoder (VQ-VAE)
VQ-VAE는 Vector Quantization을 통해 VAE에서 일반적으로 발생하는 문제점인 posterior collapse(powerful한 autoregressive decoder 사용 시 latent가 무시되는 현상)를 해결한 모델이다. 이를 알아보기 이전에 vector quantization에 대한 이해가 필요하다.
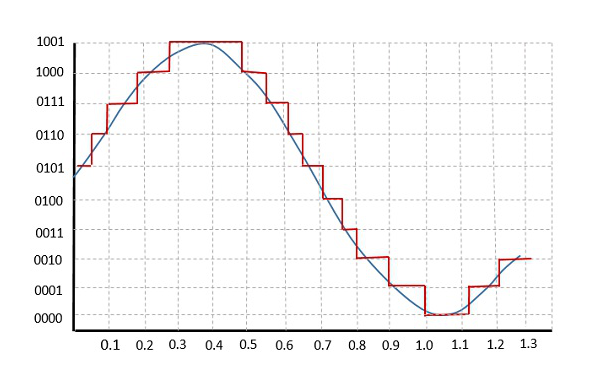
Quantization(양자화)이란, Fig 3에서와 같이 실수 전체 집합(N개, 파란색)에 해당하는 값들을 유한한 집합(K개, 빨간색)의 값으로 변환하는 개념이다.
Vector quantization은 '\(N\)개 특징 벡터 집합 \(\mathbf{x}\)를 \(K\)개 특징 벡터 집합 \(\mathbf{y}\)로 맵핑하는 함수 \(f\)'로 생각해볼 수 있다.
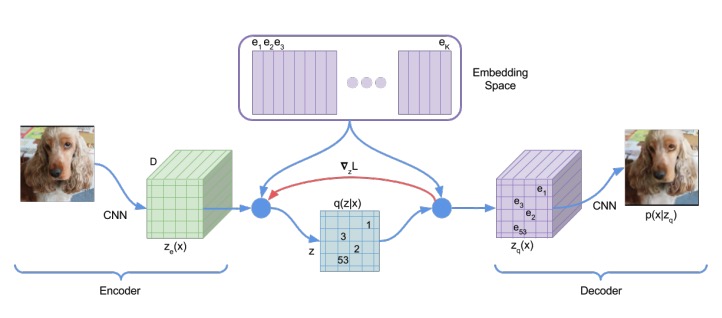
VQ-VAE는 Fig 4에서 볼 수 있듯, \(K\)개의 embedding vector로 이루어진 embedding space(=codebook)를 갖는다. 각 embedding vector의 차원은 \(D\)이다.
Encoder의 output \(z_e(x)\) 역시 \(D\)차원이며, 맵핑을 위해 다음과 같은 posterior categorical distribution을 생성한다.
\( q(z=k \vert x) = \begin{cases} 1 & \quad \text{for } k = \underset{j}{\operatorname{argmin}} \lVert z_e(x) - e_j \rVert_2 \\ 0 & \quad \text{otherwise} \end{cases} \)
즉, encoder의 output이 embedding vector 중 가장 가까운 index에 해당하는 값은 1, 다른 값은 0이 되는 것이다. 이후 \(e_k\)로 맵핑된다.
Decoder는 더 간단하다.
\( z_q(x) = e_k, \quad \text{where } k = \underset{j}{\operatorname{argmax}} \lVert z_e(x) - e_j \rVert_2 \)
Decoder에서는 방금 encoder의 output \(z_e(x)\)와 가장 가까웠던 \(e_k\)를 입력으로 주어 이미지를 복원한다.
VQ-VAE의 동작 방식을 예로 들어서 설명하자면, 아래와 같다.

Fig 5에서 빨간색으로 표시한 discrete code가 \(e_k\)에 해당하는 것이다.
Loss는 다음과 같다.
\( \log (p(x \vert q(x))) + \lVert \operatorname{sg}[z_e(x)] - e \rVert_2^2 + \beta \lVert z_e(x) - \operatorname{sg}[e] \rVert_2^2 \)
- \( \log (p(x \vert q(x)))\) : Reconstruction loss
- \( \operatorname{sg}\) (Stop Gradient) : 해당 term은 weight update를 하지 않음
- \( \lVert \operatorname{sg}[z_e(x)] - e \rVert_2^2 \) : Codebook alignment loss → embedding vector \(e\) (예시에서의 \(e_k\))가 해당하는 encoder 출력 \(z_e(x)\)와 가까워지도록 함
- \( \lVert z_e(x) - \operatorname{sg}[e] \rVert_2^2 \) : Codebook commitment loss → encoder 출력 \(z_e(x)\)가 embedding vector \(e\)와 가까워지도록 함
VQ-VAE 학습 시에는 \(z\)가 uniform prior라고 가정하는데, 학습 후에는 \(z\)에 autoregressive distribution을 적용하여 다양한 generation task에 VQ-VAE를 활용할 수 있다. 예를 들어, \(z\)에 PixelCNN을 사용하여 image를 생성하거나, WaveNet을 사용하여 audio를 생성할 수 있다.
Flow-based Generative Models
AE, VAE, Normalizing flow model의 공통점은 likelihood를 기반(loss)으로 학습을 진행한다는 점이다.
특히 VAE의 경우에는 변분 추론(Variational inference)을 통해 계산이 어려운 (latent variable의) posterior \(p(\mathbf{z} \vert \mathbf{x})\)를 계산이 쉬운 \(q(\mathbf{z} \vert \mathbf{x})\)로 근사한다. (자세한 내용은 링크를 참조하자.)
VAE에서는 \(q(\mathbf{z})\)를 가장 간단한 분포인 정규분포로 정하는데, normalizing flow model에서는 정규분포 대신에 복잡한 확률 분포를 모델링하도록 한다.
Normalizing Flow
Normalizing flow란, 단순한 형태의 gaussian \(\mathbf{z}\)에 invertible 연산 \(f\)를 적용하여 복잡한 확률 분포 \(p(\mathbf{x})\)를 모델링하는 방법이다.
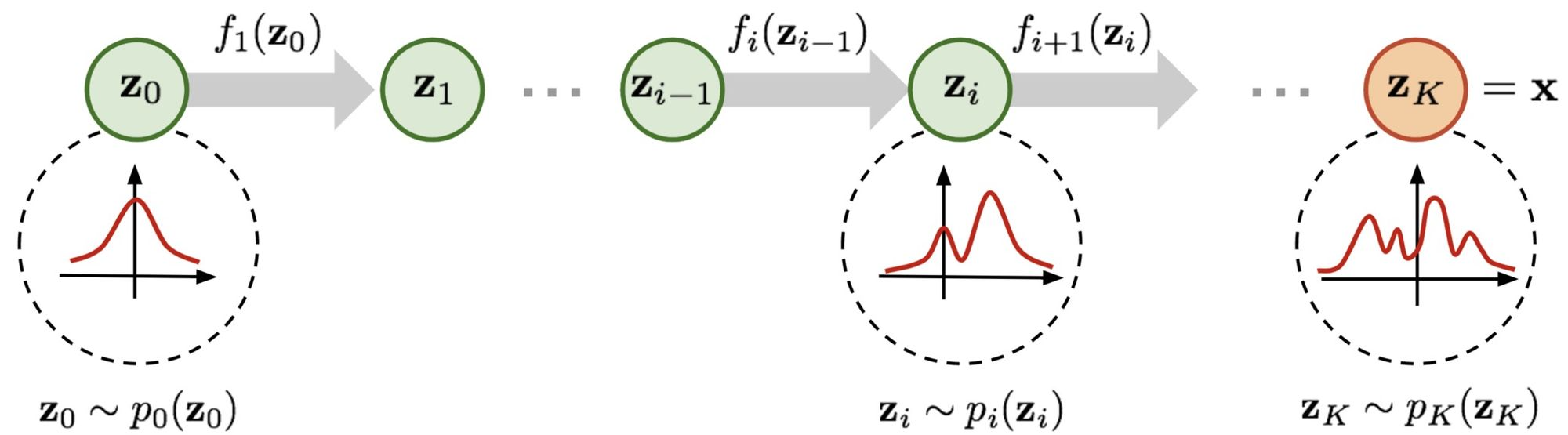
Fig 6에서 flow는 연산 \(f\)를 거치는 각각의 step을 말하고, normalizing flow는 위 그림 전체의 과정을 말한다.
Change of Variables Theorem
Single random variable \(z\)에 대해, \(z \sim \pi(z)\)라 하고, invertible 일대일 함수 \(f\)를 통해 새로운 random variable \(x = f(z)\)를 구성한다고 하자. 이때 \(x\)의 확률 분포 \(p(x)\)는 다음과 같이 정의할 수 있다.
\( \int p(x) dx = \int \pi(z) dz = 1 \)
\( p(x) = \pi (z) \left\vert \cfrac{dz}{dx} \right\vert = \pi (f^{-1} (x)) \left\vert \cfrac{d f^{-1}}{dx} \right\vert = \pi (f^{-1}(x)) \left\vert (f^{-1})^\prime (x) \right\vert \)
Multivariable일 경우, 다음과 같이 구한다.
\( \mathbf{z} \sim \pi(\mathbf{z}), \quad \mathbf{x} = f(\mathbf{z}), \quad \mathbf{z} = f^{-1} (\mathbf{x}) \)
\( p(\mathbf{x}) = \pi (\mathbf{z}) \left\vert \operatorname{det} \cfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert = \pi (f^{-1}(\mathbf{x})) \left\vert \operatorname{det} \cfrac{df^{-1}}{d \mathbf{x}} \right\vert \)
이를 통해 알지 못하는 확률 분포 \(p(\mathbf{z})\)를 \(\mathbf{z}\)의 확률밀도함수로 표현 가능하다.
Normalizing Flow
이제 주어진 간단한 분포 \(p_0(z_0)\)로부터 복잡한 분포 \(p_k(z_k)\)를 모델링해보자. Change of variables theorem을 그대로 활용하면 다음과 같이 나타낼 수 있다.
\( \mathbf{z}_{i-1} \sim p_{i-1}(\mathbf{z}_{i-1}) \mathbf{z}_i = f_i (\mathbf{z}_{i-1}), \quad \text{where } \mathbf{z}_{i-1} = f_i^{-1} (\mathbf{z}_i) \)
\( p_i(\mathbf{z}_i) = p_{i-1} (f_i^{-1}(\mathbf{z}_i)) \left\vert \operatorname{det} \cfrac{d f^{-1}}{d \mathbf{z}_i} \right\vert \)
여기서 \(p_i(\mathbf{z}_i)\) 식을 \(\mathbf{z}_{i-1}\)에 대한 식으로 나타내어 이전 distribution으로 복잡한 분포를 모델링(flow 과정)하는 수식을 만들 수 있다.
\( \begin{align*} p_i(\mathbf{z}_i) &= p_{i-1} (f_i^{-1}(\mathbf{z}_i)) \left\vert \operatorname{det} \cfrac{d f^{-1}}{d \mathbf{z}_i} \right\vert \\ &= p_{i-1}(\mathbf{z}_{i-1}) \left\vert \operatorname{det} \left( \cfrac{d f_i}{d \mathbf{z}_{i-1}} \right)^{-1} \right\vert \quad \quad \because \text{Inverse function theorem} \\ &= p_{i-1}(\mathbf{z}_{i-1}) \left\vert \operatorname{det} \cfrac{d f_i}{d \mathbf{z}_{i-1}} \right\vert^{-1} \quad \quad \because \text{property of Jacobians of invertible func} \end{align*} \)
참고로 위 유도과정에서는 다음 두 가지 개념을 이용했다.
- Inverse function theorem
- \(y = f(x)\)이고, \(f\)가 invertible function이라면,
- \( \cfrac{d f^{-1}(y)}{dy} = \cfrac{d x}{d y} = \left( \cfrac{d y}{d x} \right)^{-1} = \left( \cfrac{df(x)}{dx} \right)^{-1} \)
- Jacobian of invertible functions
- \( \operatorname{det}(\mathbf{M}) \operatorname{det}(\mathbf{M}^{-1}) = \operatorname{det}(\mathbf{M} \times \mathbf{M}^{-1}) = \operatorname{det}(\mathbf{I}) = 1 \)이므로
- \( \operatorname{det}(\mathbf{M}^{-1}) = (\operatorname{det}(\mathbf{M}))^{-1} \)
위 식에 log를 취하면 아래와 같다.
\( \log p_i(\mathbf{z}_i) = \log p_{i-1} (\mathbf{z}_{i-1}) - \log \left( \operatorname{det} \cfrac{d f_i}{d \mathbf{z}} \right) \)
이러한 과정을 K번 반복하면 \(\mathbf{z}_K\), 즉 \(\mathbf{x}\)의 분포를 구할 수 있다.
\( \mathbf{x} = \mathbf{z}_K = f_K \circ f_{K-1} \circ \cdots \circ f_1(\mathbf{z}_0) \)
\( \begin{align*} \log p(\mathbf{x}) = \log \pi_K(\mathbf{z}_K) &= \log \pi_{K-1}(\mathbf{z}_{K-1}) - \log \left\vert \operatorname{det} \cfrac{d f_K}{d \mathbf{z}_{K-1}} \right\vert \\ &= \log \pi_{K-2}(\mathbf{z}_{K-2}) - \log \left\vert \operatorname{det} \cfrac{d f_{K-1}}{d \mathbf{z}_{K-2}} \right\vert - \log \left\vert \operatorname{det} \cfrac{d f_K}{d \mathbf{z}_{K-1}} \right\vert \\ &= \cdots \\ &= \log \pi_0(\mathbf{z}_0) - \sum\limits_{i=1}^K \log \left\vert \operatorname{det} \cfrac{d f_i}{d \mathbf{z}_{i-1}} \right\vert \end{align*} \)
이렇게 정의한 \(\log p(\mathbf{x})\)를 활용하여 학습 데이터셋 \(\mathcal{D}\)에 대한 negative log-likelihood(NLL) loss를 정의할 수 있다.
\( \mathcal{L}(\mathcal{D}) - \cfrac{1}{\left\vert \mathcal{D} \right\vert} \sum\limits_{ \mathbf{x} \in \mathcal{D}} \log p(\mathbf{x}) \)
Flow-based generative model
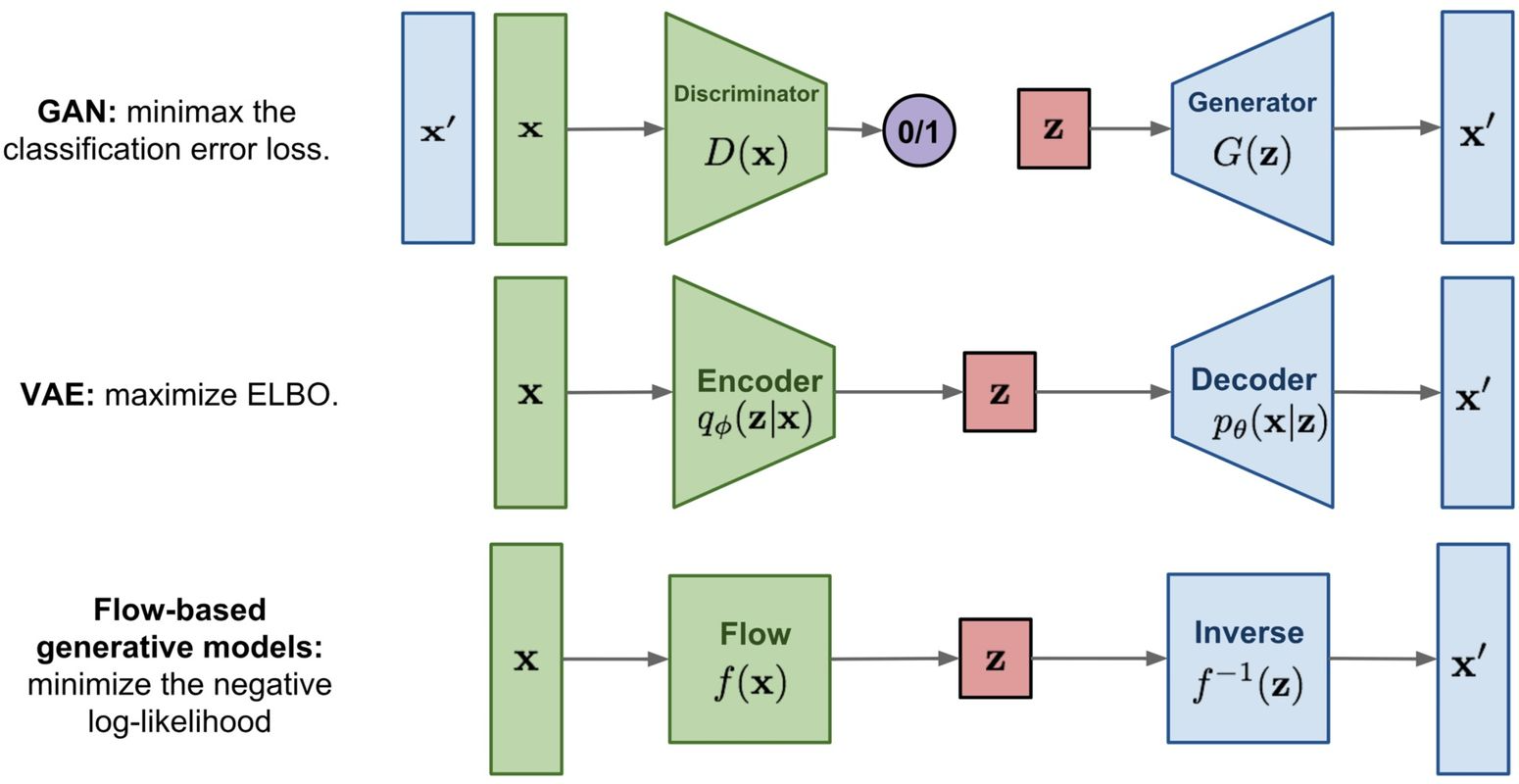
GAN과 VAE는 데이터를 학습할 때 데이터 \(\mathbf{x}\)의 분포를 implicit하게 학습한다. 하지만, flow-based generative model의 경우에는 normalizing flow(flow \(f\)와 inverse flow \(f^{-1}\))를 통해 데이터 분포를 explicit하게 학습한다.
단, normalizing flow를 적용하기 위해서는 다음과 같은 조건을 충족해야 한다. (실제로 이 조건들을 충족하기가 쉽지 않다.)
- 연산 \(f\)의 inverse 계산이 가능해야 한다.
- Jacobian determinant의 계산이 가능해야 한다.
Flow-based generative model에는 대표적으로 RealNVP, Glow 등의 모델이 있다.
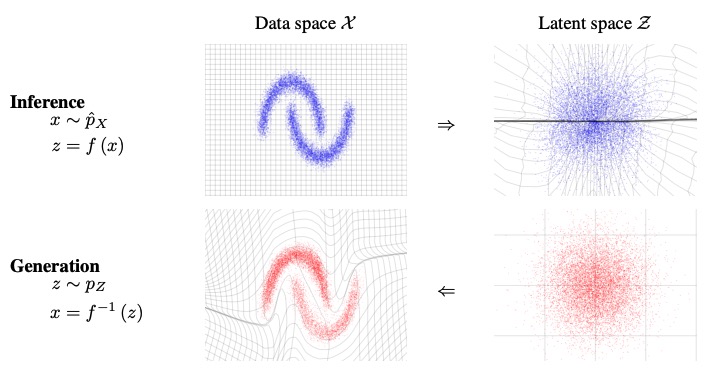
Fig 8은 RealNVP의 inference, generation 과정을 나타낸다. RealNVP는 고차원에서의 determinant, Jacobian 계산의 효율성을 위해 invertible function(transformation)에 '(affine) coupling layer'를 사용한다. Affine coupling layer에서 input의 반은 target distribution으로 맵핑하고, 나머지 반은 그대로 둔다. 이를 통해 inverse, determinant 계산이 가능하면서도 모델의 flexibility를 높여준다.
Diffusion Models
Diffusion model은 data에서 noise를 조금씩 더해가며 완전한 noise로 만드는 forward process(=diffusion process)와 반대로 noise로부터 조금씩 복원해가면서 data를 만들어내는 reverse process로 이루어진다.
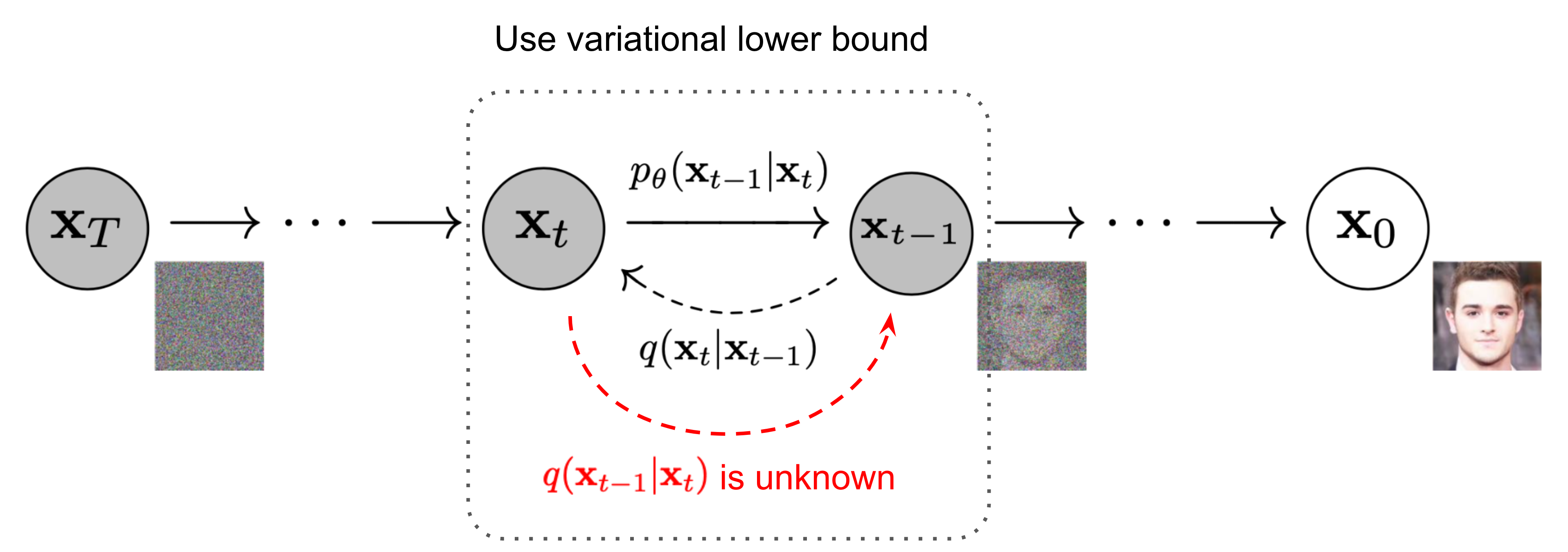
Architecture of Diffusion
\(\mathbf{x}_0\)는 실제 data, \(\mathbf{x}_T\)는 최종 noise, 그 사이 \(t\) 시점의 \(\mathbf{x}_t\)는 데이터에 noise가 더해진 상태의 latent variable으로 볼 수 있다.
여기서 forward process는 \(q\), reverse process는 \(p\)이고, \(p\)를 학습함으로써 noise \(\mathbf{x}_T\)에서 data \(\mathbf{x}_0\)를 복원하는 과정(image generation)을 학습한다. 수학적으로는 실제 data의 분포 \(p(\mathbf{x}_0)\)를 찾아내는 것이 목적이다.
언뜻 봤을 때 위의 flow-based generative model의 normalizing flow와 비슷해 보이는데, flow-based model과 diffusion model은 공통적으로 간단한 distribution을 target distribution으로 바꾸려 하지만, 그 방식이 다르다. Flow-based model에서는 invertible function(transformation)을 사용하는 반면, diffusion에서는 그럴 필요는 없다. Diffusion model에서는 target distribution을 가능한 가깝게 근사하는 것이 목적이다.
Reverse process \(p\)를 곧바로 모델링하기는 힘들기 때문에, 학습된 Gaussian transition을 활용한 Markov chain 형태로 \(p\)를 근사한다.
\( p_\theta (\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod\limits_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t), \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) := \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta (\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta (\mathbf{x}_t, t)) \)
- \(\boldsymbol{\mu}_\theta, \boldsymbol{\Sigma}_\theta\) : Learnable parameters
- Starting point (noise의 분포) : \(p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \boldsymbol{0}, \mathbf{I}) \)
Forward process \(q\)의 정보를 활용해서 reverse process를 학습하기 때문에, 이 과정의 분포도 알아야 한다. Data에 Gaussian noise를 조금씩 더하는 Markov chain 형태이다.
\( q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) := \prod\limits_{t=1}^T q(\mathbf{x}_t \vert \mathbf{x}_{t-1}), \quad q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t ; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I} \)
- \(\beta_1, \dots, \beta_T\) : Variance schedule → reparameterization을 통해 학습 또는 constant(hyperparameter)
이와 같이 forward process(diffusion process)를 표현하게 되면 data가 주어졌을 때 임의의 times step \(t\)에서의 data \(\mathbf{x}_t\)를 sampling할 수 있다. data \(\mathbf{x}_0\)가 주어졌을 때, \(\mathbf{x}_t\)의 분포를 다음과 같이 구할 수 있기 때문이다.
\( q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t) \mathbf{I} \)
- \(\alpha_t = 1 - \beta_t\)
- \(\bar{\alpha}_t = \prod_{i=1}^t \alpha_i\)
Loss of Diffusion
Diffusion model의 목적은 앞에서도 언급했듯이 실제 data의 분포 \(p(\mathbf{x}_0)\)를 찾는 것이다. 따라서 이 분포의 likelihood를 최대화(negative log likelihood를 최소화)하는 것이 목적이다.
\( \mathbb{E}[- \log p_\theta(\mathbf{x}_0)] \leq \mathbb{E}_q \left[ - \log \cfrac{p_\theta(\mathbf{x}_{0:T}}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \right] = \mathbb{E}_q \left[ - \log p(\mathbf{x}_T) - \sum\limits_{t \geq 1} \log \cfrac{p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)}{q(\mathbf{x}_t \vert \mathbf{x}_{t-1})} \right] =: L \)
부등호 증명은 논문을 참조하고, 등호는 Markov property에 의해 성립한다.
좀 더 식을 정리하면 아래와 같이 Gaussian 분포 간의 KL divergence 형태로 loss function을 변형할 수 있다.
\( \mathbb{E}_q \left[ \underbrace{D_{\text{KL}} ( q(\mathbf{x}_T \vert \mathbf{x}_0) \Vert p(\mathbf{x}_T))}_{L_T} + \sum\limits_{t > 1} \underbrace{D_\text{KL} (q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \Vert p_\theta (\mathbf{x}_{t-1} \vert \mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta (\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} \right] \)
- \(L_T\) : \(p\)가 생성하는 noise \(\mathbf{x}_T\)와 \(q\)가 (data \(\mathbf{x}_0\)가 주어졌을 때) 생성하는 noise \(\mathbf{x}_T\) 간의 KL divergence
- \(L_{t-1}\) : reverse process \(p\)와 forward process \(q\)의 KL divergence
- \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\) term이 갑자기 어떻게 도출됐는지는 논문을 참조하자.
- \(L_0\) : Latent \(\mathbf{x}_1\)로부터 data \(\mathbf{x}_0\)를 추정하는 negative likelihood
여기까지가 2D image generation에서 좋은 성능을 나타냈던 diffusion model에 대한 간략한 설명이다. 이를 보완한 DDPM, D3PM 등 다양한 변형 모델들이 있는데, 기회가 된다면 추후에 따로 다뤄보도록 하겠다.
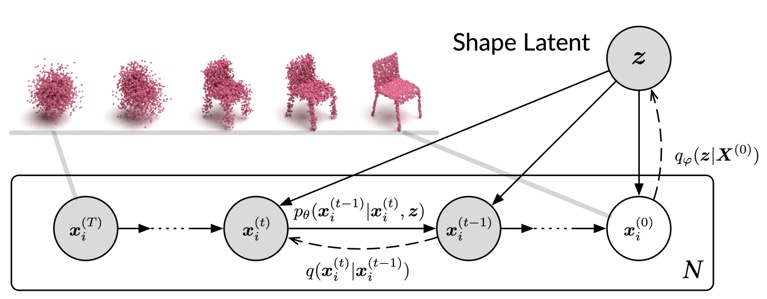
3D domain에서는 Fig 10과 같이 diffusion을 직접적으로 point cloud generation에 활용한 diffusion point cloud model 등이 있고, diffusion의 개념을 활용하여 shape generation task 등에 적용한 다양한 연구가 진행되고 있다.








최근댓글