딥러닝 기초 - GNN

 

 

목차

 

 

자주 잊어버리는 딥러닝 기초 내용을 여러 포스팅에 걸쳐 간단하게 정리해보려 한다. 다룰 내용은 크게 아래와 같다.

• Introduction
• Elements of ML
• Multi-layer Perceptron
• Model Selection
• CNN
• GNN
• RNN

 

딥러닝 강의에서는 보통 위 내용 중 GNN을 뺀 나머지 내용에 대해 다룬다. (적어도 내가 접했던 딥러닝 강의들은 그러했다.) 머신러닝 기초(regression, classification), MLP, CNN, RNN, Generative model 등..

하지만, graph 데이터를 다루는 GNN 또한 기본적인 내용은 알아둘 필요가 있다. 그 이유를 GNN이 갖는 inductive bias와 관련하여 이 포스팅에서 알아보자.

 

 

 

 

Graph Data

 

일반적인 '함수의 그래프'와 같이 데이터를 시각적으로 표현하는 것과 달리, Computer Science에서 graph는 데이터를 표현하는 하나의 구조이다. 기본적으로 이 구조는 \(\mathcal{G} = \{\mathcal{V}, \mathcal{E}\} \)로 표현하며, 이 식의 의미는 그래프는 '노드(node, vertex)와 노드 사이를 잇는 엣지(edge)로 이루어진다'라는 것이다.

Node는 보통 entity, object, instance 등을 나타낸다. 예를 들어, 어떤 scene에서의 object, 논문들 간의 인용 관계를 나타낸 citation graph에서는 paper가 이에 해당한다.

Edge는 두 node 간의 관계(relationship)를 나타낸다. 위와 같은 맥락으로, scene에서 object 간의 위치관계(object 1은 object 2의 오른쪽에 위치한다), 인용 관계(paper 1에서 paper 2를 인용하였다) 등을 나타낸다.

Node, edge 이외에도 property가 존재하는데, 이는 node에 대한 특성을 나타낸다. Scene에서 해당 object의 색상, texture 등을 예로 들 수 있다.

 

Scene을 나타낼 때 image로 나타냈을 때와 graph로 나타냈을 때의 차이점을 살펴보자.

Image는 grid space, 즉 pixel을 통해 정해진 크기의 boundary 내에서 정보를 표현한다. 이에 반해 graph는 scene에 등장하는 object를 node로, node 간의 관계를 edge로 표현한다. 따라서 graph는 image에 비해 어떠한 '관계 정보(relationship information)'를 표현하고, 다루기에 적합하다. (Image에서는 grid간의 관계는 표현할 수 있겠으나, object 간의 relationship을 표현하려면 segmentation 등의 추가적인 과정을 거쳐야 한다.)

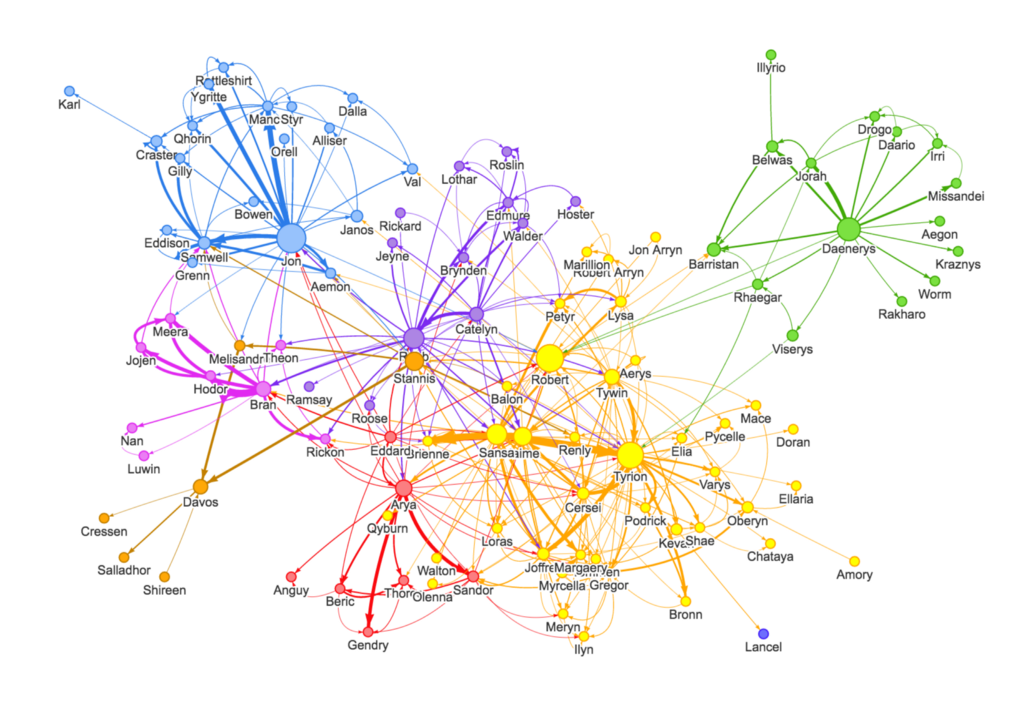
필자가 vision 분야에 관심이 많아서 이와 관련하여 graph data를 설명했는데, 사실 graph는 scene에 대한 정보보다는 social network, molecule structure 등에 더 많이 사용된다.

 

Fig 1. Graph Data - Social Network

 

Fig 2. Graph Data - Molecules

 

Graph theory에서 그래프 구조를 나타낼 때 사용하는 표현은 다음과 같다.

\( \mathcal{G} = ( \mathcal{V}, \mathcal{E}) \)

• \(\mathcal{V}\) : node(vertice)들의 집합
• \(\mathcal{E}\) : edge(arc)들의 집합
  • \((u,v) \in \mathcal{E}\) : node \(u\)와 node \(v\)를 잇는 edge
    • undirected : 방향성이 없는 경우 (symmetric relation)
    • directed : 방향성이 있는 경우 (asymmetric relation)
    • Weighted edge : connectivity에 강도가 존재하는 경우

 

 

 

Graph Representation

 

이러한 graph data를 나타내기 위한 방법은 여러가지가 있다.

먼저 가장 단순한 방법으로 adjacency matrix가 있다. 이는 Fig 2와 같이 행렬을 사용하여, (undirected, non-weigted edge라 가정했을 때) \(i\)번째 node와 \(j\)번째 node가 연결되면 해당 요소 \(\mathbf{A}_{ij} = \mathbf{A}_{ji} = 1\), 아니면 \(0\)의 값을 갖는 행렬이다. 이는 수학적으로 그래프를 표현하기 위해 가장 일반적으로 많이 사용하는 방법이다.

하지만, adjacency matrix로 graph 구조를 나타낼 경우 비효율적이라는 단점이 있다. Adjacency matrix는 매우 sparse하다. 즉, 실제 데이터를 생각해보면 node끼리 연결되어있지 않은 경우가 대부분이므로, 몇 없는 연결관계를 나타내기 위해 object 개수 \(n\)에 대해 \(n^2\)만큼의 memory가 필요하다.

 

따라서, adjacency list라는 방법으로 edge(node 간 연결성)을 표현해줄 수 있다. \([(u, v), (x, y), \dots]\)와 같이, 두 node 간의 edge를 tuple 형태로 표현해주는 방법이다.

실제로 (구현 단계에서) DGL(Deep Graph Library)에서는 graph를 adjacency list로 나타낸다.

 

그리고, node와 edge는 사용자가 지정한 feature를 가질 수 있다. 이는 node나 edge의 구체적인 특성을 수학적으로(벡터로) 나타낸 개념이다.

 

 

 

Tasks in Graph Structured Data

 

Graph data를 활용한 task는 크게 다음과 같이 나눌 수 있다.

• Graph-level task
  • 예시 : graph에 ring 구조가 포함되어 있는가?
• Node-level task
  • 예시 : 각 node의 label은 무엇인가?
• Edge-level task
  • 예시 : 두 entity 간의 관계는 무엇인가?

 

 

 

 

Principles in Graph Data

 

이러한 graph data를 다루는 딥러닝 네트워크인 GNN은 permutation invariance라는 inductive bias를 갖고 있다. GNN의 inductive bias와 관련하여 graph data가 갖는 성질을 알아보자.

먼저, 기본적으로 graph data를 다루는 GNN은 entity 간의 relationship 정보가 보존되어야 한다. 이전 글을 복기해보면, CNN에서는 locality를 가지는데, 이로 인해 pixel 각각에 대한 정보(pixel들 간의 정보)를 잃을 수 있었다. 하지만 graph에서는 주어진 node간의 정보는 계속해서 유지된다는 특성을 갖는다.

다음으로, Graph data는 permutation equivariance라는 성질을 갖는다. 여기서 permutation은 node(또는 node feature)의 순서가 바뀜을 의미하고, invariance는 순서가 바뀌어도 결과가 같음을, equivariance는 순서가 바뀌었을 때 결과도 같이 바뀜을 의미한다. 서로 다른 두 개념이 어떻게 graph data와 GNN에 존재하는지 알아보자.

 

Permutation Invariance

\( \phi(\pi \mathbf{x}) = \phi(\mathbf{x}) \)

여기서 \(\pi\)는 permutation, 즉 순서가 바뀌는 것을 의미한다. (즉, node 순서가 바뀌어도 output은 그대로이다.)

어떤 graph \(\mathcal{g}_1\)과 동일한 구조를 가졌지만 노드의 순서가 바뀐 \(\mathcal{g}_2 = \pi \mathcal{g}_1\)가 있을 때, GNN 결과 embedding은 같다. 이것이 바로 GNN이 갖는 permutation invariance 성질이다.

 

Permutation Equivariance

\( \phi(\pi \mathbf{x}) = \pi \phi(\mathbf{x}) \)

위 식은 node 순서가 바뀌었을 때 output의 순서도 바뀜을 의미한다.

 

Fig 3. Permutation Equivariance

 

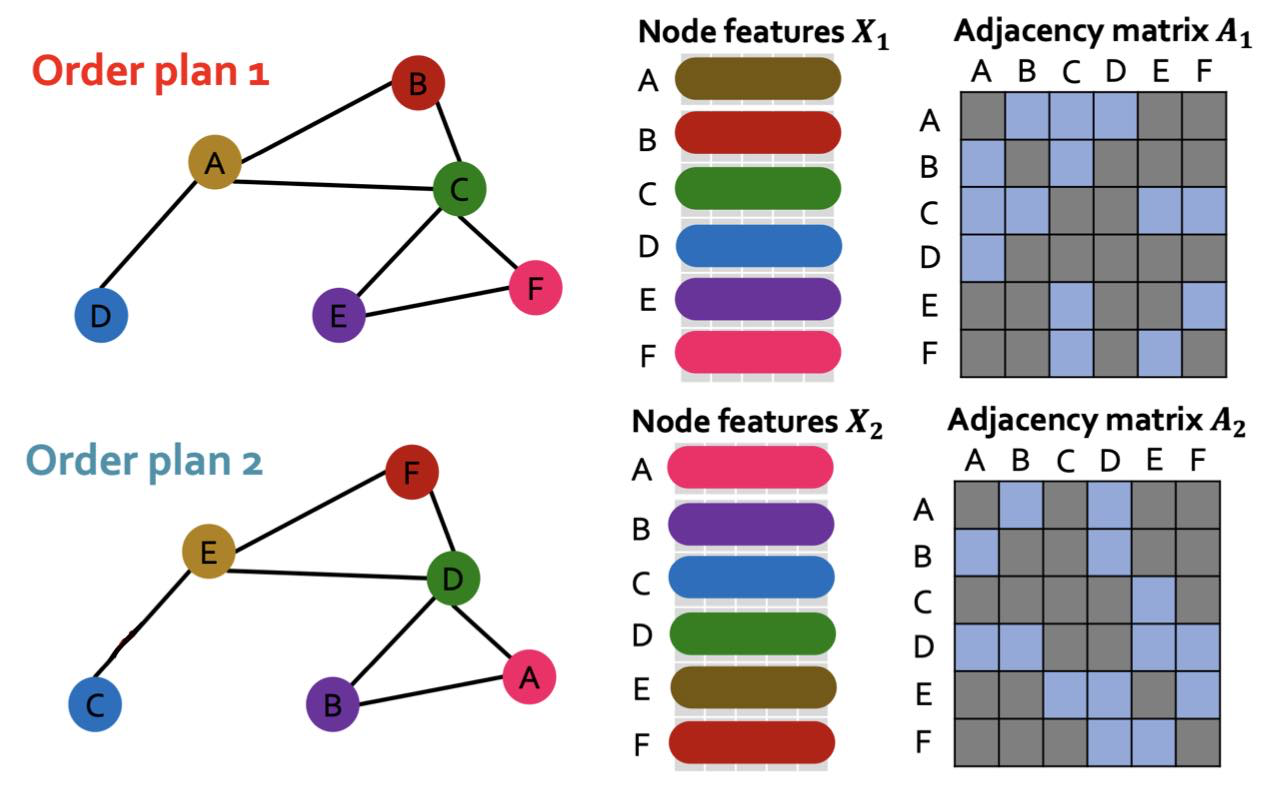
위 그림과 같이, graph data에서 node 순서가 바뀌었을 때 node feature의 순서도 (adjacency matrix가 바뀜과 함께) 바뀌게 된다. 이러한 성질을 permutation equivariance라 한다.

 

GNN 과정에서의 두 개념을 CNN에서와 비교해보며 이해해보자.

 

Fig 4. GNN Process

 

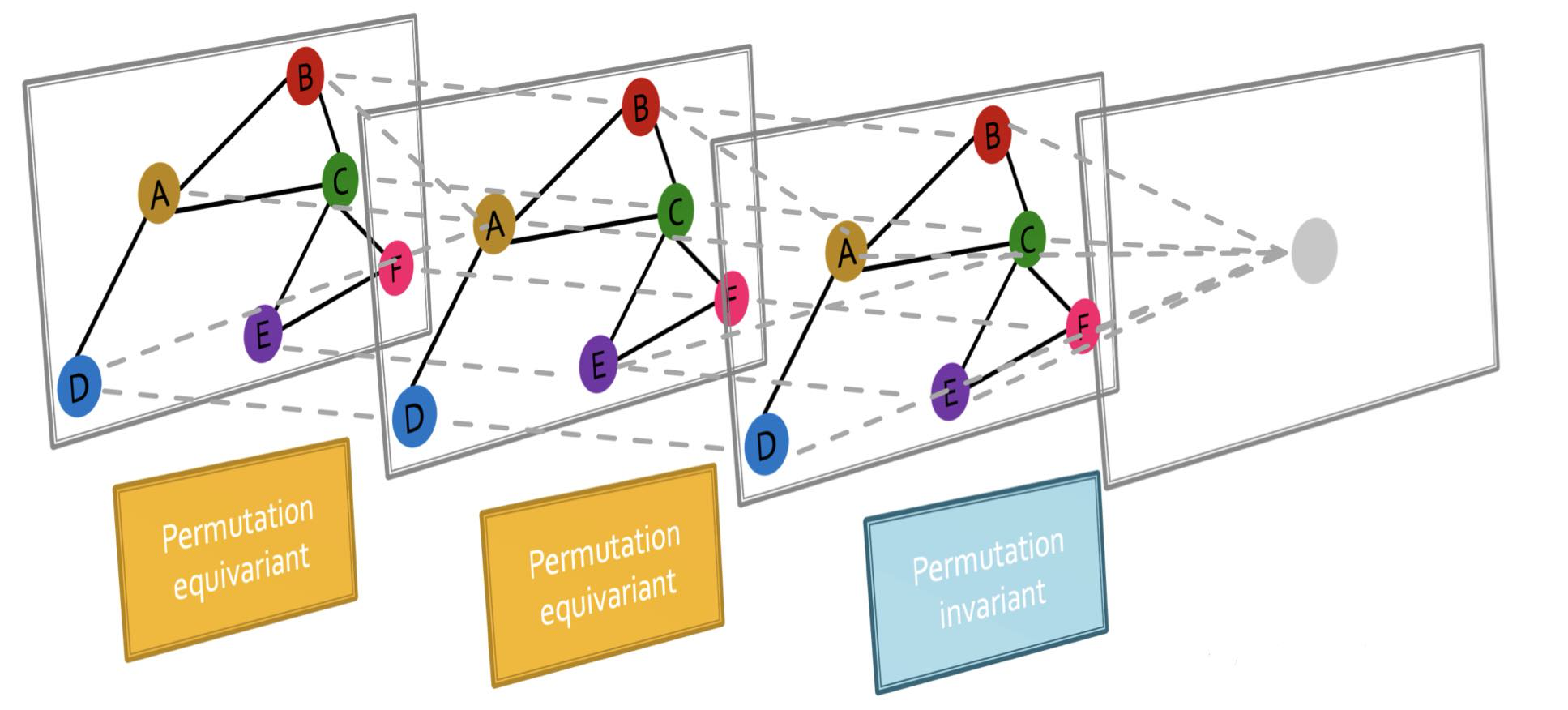
GNN은 permutation equivariant function과 permutation invariant function으로 이루어져 있다. Fig 4에서 GNN 과정을 나타내고 있는데, node A의 embedding을 얻는 게 GNN의 최종 목표라 가정하자. (마지막 회색 원을 node A의 embedding이라 생각해보자.)

 

Permutation invariant function은 GNN의 최종 목표인 target node의 embedding을 뽑을 때와 관련된 개념이다. node의 순서가 어떻게 바뀌던 간에 그 구조는 똑같으므로 같은 정보를 포함하게 될 것임을 의미한다. (예를 들어, Fig 4의 그림에서 node의 labeling이 Fig 3에서처럼 바뀐다고 해도 graph의 구조(node의 연결 관계)를 나타내는 정보는 변하지 않는다.)

 

layer 간의 연산에서는 permutation equivariant function이 사용되는데, 이는 graph data의 성질과 관련된 것이다. node 순서가 바뀜에 따라, Fig 3에서처럼 그 결과 node embedding의 순서도 같이 바뀌는 것을 의미한다.

이를 이해하기 위해서는 message passing의 개념을 이해해야 한다. Message passing 개념과 GNN 관련 더 깊은 내용은 Machine Learning with ML 강의 내용을 정리한 카테고리를 참조하자.