딥러닝 기초 - Model Selection

 

목차

 

자주 잊어버리는 딥러닝 기초 내용을 여러 포스팅에 걸쳐 간단하게 정리해보려 한다. 다룰 내용은 크게 아래와 같다.

• Introduction
• Elements of ML
• Multi-layer Perceptron
• Model Selection
• CNN
• GNN
• RNN

 

 

 

 

 

Model Selection

 

앞선 포스팅에서 머신러닝의 고질적인 문제중 하나로 overfitting, underfitting 문제와 data mismatch 문제를 언급했다.

Training error를 낮추기 위해 \( \underset{\mathbf{w}}{\min} \mathcal{L} (\mathcal{M}(\mathbf{w}), \mathcal{D}_{\text{train}}) \)로 optimization을 진행하고, training error와 test error 간의 차이를 줄이기 위해 \( \underset{\mathbf{w}}{\min} \mathcal{L} \left( \mathcal{M}(\mathbf{w}), \mathcal{D}_{\text{test}} \right)\) 또는 \(p_{\text{train}} \approx p_{\text{test}} \)와 같은 generalization 과정을 거친다고 하였다.

 

이번에는 overfitting을 피하면서 모델을 잘 학습시키는 방법과 좋은 모델을 고르기 위한 여러 방법들을 알아보자.

 

 

 

 

Data Augmentation

 

딥러닝의 효과를 보기 위해서는 엄청난 수의 데이터가 필요하다.

 

Fig 1. Data Size and Model Performances

 

만약 데이터가 조금 적다고 해도, 현재 갖고있는 데이터에 transition, rotation, cropping, flipping 등을 적용하여 데이터 수를 늘리는 data augmentation을 통해 해결할 수 있다. 실제로 data 부족 문제를 해결하기 위한 가장 좋은 방법이 이 방법이다. 딥러닝에도 잘 맞고, network의 hyperparameter를 튜닝하는 것보다 훨씬 간단하다.

 

단, 한 가지 주의할 점은 데이터에 대한 domain knowledge가 필요하다. 예를 들어, 숫자 손글씨 데이터가 부족하다고 하여 무턱대고 rotation을 통해 데이터를 늘렸다가는 모델이 6과 9를 구분하지 못할 것이다.

 

 

 

 

Weight Decay (L2 Regularization)

 

Weight decay는 overfitting을 줄일 수 있는 또다른 방법이다. 아래와 같이 loss function에 weight decay term(weight parameter의 L2 norm의 제곱)을 추가한다.

\( \mathcal{L}(\boldsymbol{\theta}, \mathcal{D}_{\text{train}}) + \lambda \lVert \boldsymbol{\theta} \rVert_2^2 \)
\( \text{Gradient descenet} : \mathbf{w} \leftarrow \mathbf{w} - \eta \nabla_{\mathbf{w}} (\mathcal{L} + \lambda \lVert \mathbf{w} \rVert_2^2) = (1 - \eta \lambda)\mathbf{w} - \eta \nabla_{\mathbf{w}} \mathcal{L} \)

• \(\lambda\) : Weight decay coefficient
• \(\lambda \lVert \boldsymbol{\theta} \rVert_2^2\) : Weight decay term
• \(\eta\) : learning rate

수식에서 볼 수 있듯이, weight decay를 길게 적용할수록(coefficient가 커질수록) weight parameter의 영향이 작아진다(vanishing). Weight decay는 optimizer 선언 시에 argument로 간단하게 적용할 수 있다.

 

 

 

 

Dropout

 

Dropout은 training 시에 hidden variable간의 연결의 일부를 끊음으로써 overfitting을 막는 방법이다.

 

Fig 2. Dropout

\( \tilde{w}_{ij}^{(l)} = \begin{cases} & 0 \quad \text{with probability } p \\ & w_{ij}^{(l)} \quad \text{with probability } 1-p \end{cases} \)

Prediction(Evaluation) 시에는 dropout을 적용하지 않는다.

단점은 학습이 stochastic해지고, 수렴을 방해하여 학습 시간이 늘어날 수 있다.

 

 

 

 

Early Stopping

 

Early stopping이란, training 과정에서 loss를 살펴보면서 모델이 overfitting되기 이전에 (최적의 상태일 때) 학습을 중단하는 것이다.

학습 도중에는 test dataset을 사용하면 안되므로 cross validation이 필요하다.

간단하면서도 효과적이라는 장점이 있으나, 학습 과정에 대한 heuristic이 어느 정도 필요하다.

 

 

 

 

Label Smoothing

 

Classification task에서는 overfitting과 관련된 over-confidence problem이 존재한다.

Label Smoothing을 통해 이를 해결할 수 있는데, label smoothing이란 one-hot vector(해당하는 건 1, 나머지는 모두 0)로 라벨을 부여하기 보다 smoothed label(0에서 1 사이의 값 중에 해당하는 class에 높은 값을 부여하고, 나머지 class는 낮은 값 부여, 즉 극단적이지 않게 smoothing)을 적용하는 방법이다.

\( \tilde{y} = (1 - \epsilon) y + \cfrac{\epsilon}{C} \)

• \(\epsilon\) : hyperparameter for label smoothing
• \(y\) : one-hot vector
• \(C\) : number of classes

이 방법은 부족한 data에 대해 효과가 아주 좋고, 라벨링이 잘못된 데이터에 대해서도 강인하다는 장점을 갖지만, classification task에 한정적으로 적용할 수 있다는 단점이 있다.

 

 

 

 

K-fold Cross Validation

 

이제까지 알아본 hyperparameter 이외에도 epoch(학습 총 반복) 횟수, learning rate(gradient를 따라 한 step에 얼마나 갈 것인가), mini-batch size(stochastic gradient descent에서), layer 개수, activation function, hidden variable의 차원 등 여러 hyperparameter가 존재한다.

 

이렇게 다양한 hyperparameter에 따라 모델의 성능이 달라지는데, 이중 최선의 모델을 선택하려면 어떻게 해야 할까?

이전까지 연구자들은 test(evaluation) 성능에 따라 best model을 선정했다. 하지만 이는 robust하지 않다. 고정된 test set을 통해 모델의 성능을 검증하고 hyperparameter를 수정하게 되면 결국 test set에 overfitting되는 결과를 낳기 때문이다.

이를 해결하기 위한 것이 cross validation이다. Cross validation이란, training 과정에서 training dataset을 training dataset + validation dataset으로 분리한 뒤, validation dataset을 사용하여 검증하는 방법이다. Evaluation은 test dataset으로 최종적으로 진행한다.

 

그 중에서도 k-fold cross validation은 training data를 k개의 fold로 나누어 각 fold별로 한 번씩 validation에 사용하고, 나머지는 training에 사용하는 과정을 k번 반복하는 방법이다.

 

Fig 3. K-fold Cross Validation

 

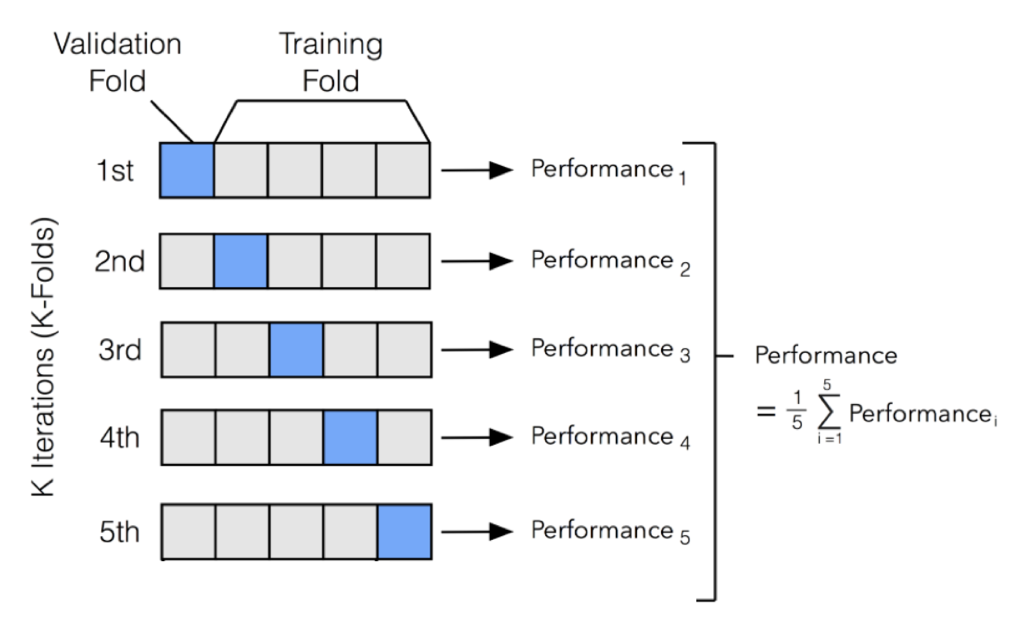
과정을 좀 더 자세히 살펴보자.

1. 전체 데이터셋을 training dataset과 test dataset으로 나눈다.
2. Training dataset을 k개 fold로 나눈다.
3. k개 fold에 대해 다음을 반복한다.
   1. 해당 fold를 validation dataset으로 사용하고, 나머지 fold들을 training dataset으로 사용한다.
   2. Training dataset으로 모델을 학습하고(training) validation dataset으로 평가한다(validation).
   3. Performance measure(accuracy 등)를 측정한다.
4. k개의 performance measure의 평균을 학습 모델의 성능으로 둔다.
5. Test dataset에 대해 평가를 진행한다(evaluation).

 

K-fold cross validation 이외에도 bootstrapping, deep ensemble 등의 방법으로 최선의 모델을 선택할 수도 있다.

 

 

 

 

Other Methods for Stable Learning

 

이외에도 overfitting을 막거나, 학습의 안정성과 효율을 높이는 다양한 방법이 있다. 간단하게 하나씩 살펴보자.

 

 

 

Batch Normalization

 

L2 regularization(weight decay)은 위에서 overfitting을 방지하기 위한 방법 중 하나라 하였다.

Optimization 시 loss 값을 줄이면서 가중치도 최소화시키는 방향으로 학습을 하기 때문에, 튀는 가중치 값이 보정되어 정규화(regularize)된다.

이와 비슷하게, batch normalization은 신경망의 깊이가 깊어졌을 때, hidden layer의 weight와 연산하는 과정에서 출력값이 들쑥날쑥해져 제대로된 학습이 이루어지지 않는 문제점을 해결해준다. Batch 뿐만 아니라 weight, layer normalization도 있다. 수식으로 나타내면 다음과 같다.

\( \text{BN}(\mathbf{x}) = \gamma \odot \cfrac{\mathbf{x} - \hat{\boldsymbol{\mu}}_{\mathcal{B}}}{\hat{\boldsymbol{\sigma}}} + \boldsymbol{\beta} \)

• \(\gamma\) : Scaling coefficient (backpropagation을 통해 학습 가능)
• \(\boldsymbol{\beta}\) : Offsets (Shift parameter, backpropagation을 통해 학습 가능)
• \(\hat{\boldsymbol{\mu}}_{\mathcal{B}}\) : Mini-batch의 sample mean
• \(\hat{\boldsymbol{\sigma}}_{\mathcal{B}}\) : Mini-batch의 sample variance

 

어떻게 batch normalization이 효과를 보는지는 정확하지 않다. (논문에서는 'covariate shift' 개념으로 설명하고 있는데, 정확하지 않고, 다른 설명도 정확히 증명된 것이 없다고 한다.)