목차
자주 잊어버리는 딥러닝 기초 내용을 여러 포스팅에 걸쳐 간단하게 정리해보려 한다. 다룰 내용은 크게 아래와 같다.
- Introduction
- Elements of ML
- Multi-layer Perceptron
- Model Selection
- CNN
- GNN
- RNN
CNN은 이미지 데이터를 주로 다루는 딥러닝 네트워크로, 컴퓨터 비전 분야에서 많이 쓰인다.
CNN의 개념을 간단히 알아보자.
Introduction
Image Data
이전까지(MLP까지)는 data point \(\mathbf{x} \in \mathbb{R}^d\), 즉 단순히 d차원의 1d 텐서의 데이터를 다루었다.
하지만, 이미지 데이터 \(\mathbf{x} \in \mathbb{R}^{H \times W \times C}\)는 보통 3차원 텐서 형태이다. (높이, 너비, 채널)
높이와 너비 만큼의 픽셀을 갖고, 각 픽셀은 0~255의 값(혹은 이를 normalize하여 0부터 1 사이의 값)을 갖는 grid 구조이다. 이것이 보통 Red, Green, Blue (RGB) 3개의 채널 형태로 쌓여있다.

Computer Vision Tasks
Computer Vision은 이러한 이미지를 처리하는 다양한 task를 해결하는 분야이다. 대표적으로 Semantic segmentation, classification(+ localization), object detection, instance segmentation 등이 있다.

Semantic segmetation은 어떤 object인지는 상관 없이, 각 pixel이 어떤 카테고리에 속하는지를 나타내는 task이다.
Classification이란, 관심있는 하나의 object가 어떤 class에 속하는지를 구분하고, localization은 그 object의 위치까지 파악하는 task이다.
Object detection은 여러 object가 어떤 class에 속하는지를 (보통 위치와 함께) 구분하는 task이다. Instance segmentation은 object 중에서도 각 개체(instance)를 pixel별로 구분해주는 task이다.
Principles(Inductive Biases) in CNN
CNN에서는 두 가지 원리를 만족한다. 이를 CNN이 갖는 inductive bias라고도 하며, inductive bias에 대한 자세한 내용은 링크를 참조하자.
먼저, inductive bias가 (거의) 없는 MLP로 이미지 데이터를 처리한다고 해보자.

MLP는 모든 pixel에 대해 parameter가 따로 존재하여 곱 연산을 수행한다. 따라서 memory가 비효율적으로 많이 필요하고, optimization이 힘들며, overfitting할 가능성이 높아진다.
이에 반해, CNN이 이미지 데이터를 다루기에 최적화된 이유는 아래와 같은 inductive bias를 만족하기 때문이다.
Locality Principle

CNN에서 convolution 연산의 핵심인 kernel(=filter)의 사이즈는 이미지의 사이즈보다 훨씬 작다. 즉, kernel size만큼 연산을 수행하므로, kernel size보다 멀리 떨어진 pixel간에는 서로 관련이 없어진다. 이를 locality라 한다.
Spatial (Translation) Invariance

Object detection을 예로 들면, object가 어떻게 생겼는지는 object의 위치와는 관련이 없다. 즉, object의 위치가 바뀌어도 object를 알아보는 데에는 전혀 지장이 없다. Fig 4에서의 강아지와 Fig 5에서의 강아지는 위치가 바뀌었는데, 사진에 강아지가 존재한다는 사실은 똑같다. 이를 spatial invariance라 한다.
kernel(=filter)을 통해 연산을 진행할 때, kernel을 옮겨가며 (같은 parameter를 공유하면서) 모든 pixel에 대해 연산을 진행하게 된다. Fig 4에서는 \(h_i\) 부분의 patch에서 결과값이 높게 나왔다면, 이번에는 \(h_2\) 부분의 patch에서 결과값이 높게 나올 것이다. 따라서 CNN을 사용하면 강아지가 사진의 왼쪽 위에 있던, 가운데에 있떤, 오른쪽에 있던 상관없이 강아지를 인식할 수 있게 된다.
Convolution Operation
Convolution 연산이 진행되는 과정을 좀 더 알아보자. Convolution 연산(Pooling 포함)은 딥러닝 관점에서의 feature extraction(특징 추출)이다. convolution 연산을 여러 번 진행하면 이미지의 특징을 뽑은 map (feature map)을 얻게 된다.
2D Convolution
먼저 간단하게 Channel이 1인 경우, 즉 2D convolution 연산을 이해해보자.
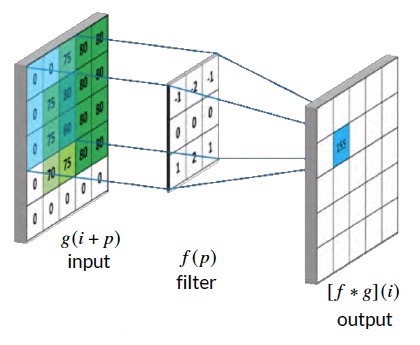
\( [f*g](i,j) = \sum\limits_{p,q} f(p,q) g(i + p, j + q) \)
\(*\)는 convolution 연산기호이다. 간단히 설명해보면, filter가 pixel 크기에 맞춰 곱하고 그 결과를 모두 더한 값이 output이 되는 것이다. 위 그림을 예로 들면, '75' 부분의 pixel에 대해 연산을 진행하면
\(0 \times -1 + 0 \times -2 + 75 \times -1 + \dots + 75 \times 2 + 80 \times 1 = 155\)
즉, output의 같은 부분에 155라는 값이 할당되는 것이다. 이 과정을 모든 pixel에 대해 반복한다.
여기서, filter(kernel)은 일반적으로 1보다 큰 사이즈(height * width)를 가지므로, 연산을 진행할수록 결과 size가 점점 작아진다.
정확하게는 결과의 shape은 kernel size \((k_h, k_w)\)에 따라
\( (h_{out}, w_{out}) = \left( h_{in} - k_h + 1, w_{in} - k_w + 1 \right) \)
이 될 것이다.
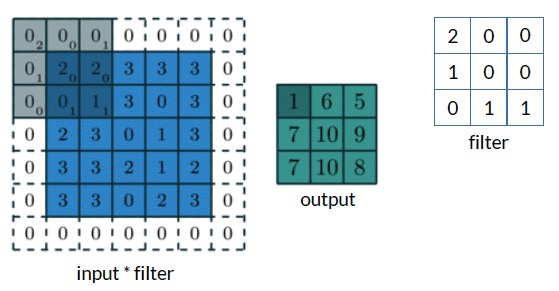
Padding은 이를 막아주는 역할을 한다. 만약 위 그림과 같이 \(3 \times 3\) filter를 사용할 때, padding size \(p=1\)로 둔다면, 이는 이미지 가장자리 부분에 0(보통 zero padding)을 추가하는 효과를 갖는다. 따라서 convolution 연산을 진행해도 output dimension이 줄어들지 않는다. (정보를 축약해주는 역할은 'pooling' 연산에서 따로 진행한다.)
또한, Striding을 통해 convolution 연산이 진행되는 step을 정해줄 수 있다. stride가 1이면 한 칸씩 kernel이 진행하고, 2면 두 칸씩 진행하는 것이다.
Stride \(s\), padding \(p\)를 고려한 output shape은 다음 식으로 계산할 수 있다.
\( (h_{out}, w_{out}) = \left( \left \lfloor{\cfrac{h_{in} - k_h + 2 p_h}{s_h}} \right \rfloor + 1, \left \lfloor{\cfrac{w_in - k_w + 2 p_w}{s_w} } \right \rfloor + 1 \right) \)
다음 예시는 \((5 \times 5)\)이미지에 대해 \((3 \times 3)\) kernel과 \((1 \times 1)\) zero padding을 사용하고, stride \(2\)로 convolution operation을 적용한 예시이다.
3D Convolution
RGB 이미지는 red, green, blue의 3개 채널을 갖는다고 하였다. 따라서 위와 같은 2d convolution을 한 차원 확장하여 3개 채널에 대해 서는 3개로 확장된 kernel로 연산을 진행한다.
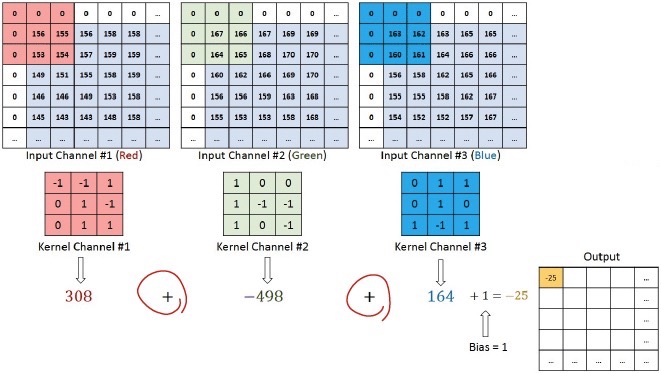
여기서, 만약 3D kernel을 여러개 사용하여 같은 input에 대해 여러 번 convolution 연산을 진행한다면, output의 shape도 3차원으로 만들 수 있다. 즉, input shape은 \((h_{in}, w_{in}, c_{in})\), output shape은 \((h_{out}, w_{out}, c_{out})\) 형태가 될 것이고, 이때 사용한 kernel은 \((k_h \times k_w)\) kernel \(c_{out}\)개를 사용한 결과일 것이다.
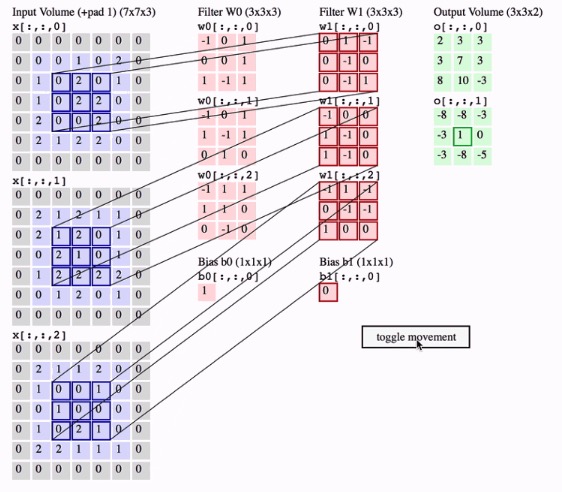
그런데, 연산의 kernel에 사용한 모든 grid의 값들은 parameter이다. 특히, neural network 관점에서 \((k_h, k_w)\) size의 kernel은 weight가 되고, bias term(scalar 값)이 하나씩 (총 \(c_{out}\)개)추가된다. 즉, convolutional layer에서 parameter의 개수는 \( (k_h \times k_w \times c_{in} + 1) \times c_{out}\)개가 된다.
Pooling
Convolution 후에는, pooling을 진행한다. Pooling의 역할은 다음과 같다.
- Aggregate information : 정보를 합쳐(축약해)준다.
- Downsampling : Feature map의 resolution을 줄여준다.
- Parameter-free operator : 학습할 parameter는 없다. (Pooling 자체를 학습하지 않는다.)
대표적인 pooling 방법은 max pooling, average pooling이 있으며, 주로 max pooling을 많이 사용한다.
Modern CNNs
CNN 기반의 다양한 네트워크가 등장했는데, LeNet, AlexNet, VGG, Inception, ResNet, DensNet 등이 있다.
모든 내용을 알아보기는 길어지니, 특정 모델에서 사용한 특별한 방법들에 대해 간단히 알아보자.
\(1\times1\) Convolution Layer
\(1\times1\) Convolution layer는 2014년 ImageNet challenge에서 구글이 제안한 Inception이라는 모델에서 사용된 개념으로, 말 그대로 \(1\times 1\) kernel(당연히 kernel 개수는 input의 channel과 같음)을 사용한 convolution 연산을 진행하는 layer이다.

따라서 Output의 size는 input과 똑같이 그대로 보존되지만, channel 수, 즉 dimension을 줄이기 위해 사용되었다.
Skip Connection
Skip connection은 Microsoft에서 제안한 ResNet에서 사용된 방법으로, CNN 뿐만 아니라 다양한 분야에서 유용하게 사용되는 방법이다. 무작정 layer를 쌓아 모델을 깊게 설계하면 오히려 overfitting되거나 optimization이 힘들어지는 문제가 생긴다.

하지만, input을 보존한 채로 layer의 결과와 더한 후에 activation funciton을 거쳐 최종 output을 낸다면 훨씬 깊은 layer를 쌓을 수 있게 되고, 따라서 모델의 성능을 안정적으로 끌어올릴 수 있게 된다. 이를 skip connection이라 한다.
\( f(\mathbf{x}) = g(\mathbf{x}) + \mathbf{x} \)








최근댓글