자주 잊어버리는 딥러닝 기초 내용을 여러 포스팅에 걸쳐 간단하게 정리해보려 한다. 다룰 내용은 크게 아래와 같다.
- Introduction
- Elements of ML
- Multi-layer Perceptron
- Model Selection
- CNN
- GNN
- RNN
목차
Non-linear Models
이전 포스팅에서 살펴본 모델들은 data를 예측하거나 분류할 때 linear function을 이용하였다.
예를 들어, binary classification task가 주어졌다고 하자. binary classification이란 두 가지를 분류(예를 들어 사진이 강아지, 고양이 둘 중 무엇인가?)하는 task이다. 이 경우, classification 모델의 학습 과정은 데이터의 두 class(강아지, 고양이)를 나누는 decision boundary(hyperplane)을 찾는 과정으로 볼 수 있다.
Fig 1은 hyperplane이 직선인 간단한 경우이다. Output을 one-hot vector로 표현하여 데이터의 차원이 고차원인 (예를 들어, 데이터 \(\mathbf{x}\)의 요소가 \(x_1, x_2, x_3\)인) 경우에도 위와 같이 나타낼 수 있다.
그런데, 만약 deision boundary가 nonlinear하다면 어떨까? 다음 그림을 보자.
이러한 경우, 위 데이터 feature를 맵핑하여 hyperplane 하나로 나뉠 수 있도록 데이터를 나타낸 공간을 변형(transform)해주어야 한다.
하지만, linear function은 이러한 맵핑을 할 수 없다. (linear transform은 affine transform이기 때문이다. 더 자세한 설명은 이 포스팅의 수준을 넘어서므로 궁금하다면 따로 검색해보도록 하자.)
From Linear to Nonlinear
예시의 데이터를 분류하는 함수를 찾기 위해서는 Fig 3와 같이 고차원 공간의 manifold를 찾아 맵핑해주어야 한다. 이러한 과정을 manifold learning이라 하고, 이를 위해 multi-layer perceptron을 사용한다.
XOR Problem and Non-linear Activation Function
Pereptron은 linear function이다. 이러한 linear function을 여러 번 사용한다고 해도 절대 Fig 4에서와 같은 XOR 문제를 해결할 수는 없다. 다음 예시를 살펴보자.
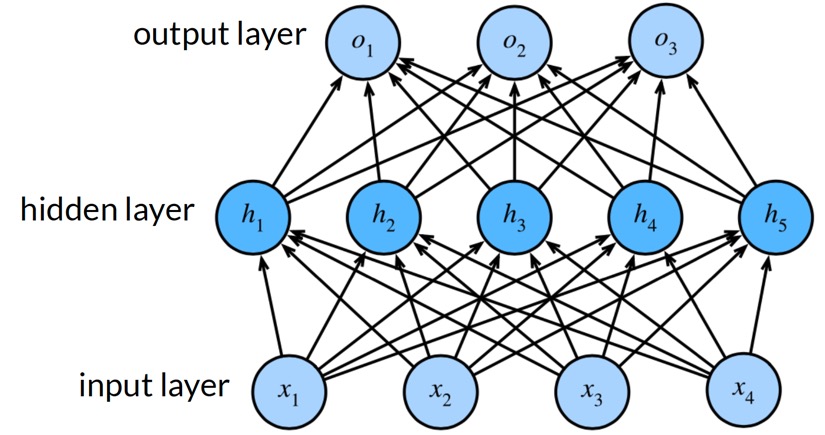
각 layer에서 일어나는 연산을 수식으로 표현해보면 아래와 같다.
\( h_j = \sum\limits_{i} w_{ij}^{(1)} x_i = \mathbf{w}_j^{(1)} \mathbf{x} \)
\( o_k = \sum\limits_{j} w_{jk}^{(2)}\mathbf{h} \)
두 함수를 합성해보아도 결국 선형 함수이므로, 결국 non-linearity를 갖지 못한다.
따라서, 아래와 같이 nonlinear activation function \(\varphi\)를 사용하여 비선형성을 부여할 수 있다.
\( h_j = \varphi \left( \sum\limits_{i} w_{ij}^{(1)} x_i \right) = \varphi ( \mathbf{w}_j^{(1)} \mathbf{x}) \)
\( o_k = \sum\limits_{j} w_{jk}^{(2)} h_j = \mathbf{w}_k^{(2)} \mathbf{h} \)
Activation function에 자주 활용되는 함수는 다음과 같다.
Activation function의 결과, ReLU는 0 이상의 값, Sigmoid는 0에서 1 사이의 값, Hyperbolic Tangent는 -1에서 1사이의 값을 가지므로, task와 상황에 따라 적절히 사용된다.
Stochastic Gradient Descent Optimization
Optimization 방법 중 하나인 Stochastic Gradient Descent (SGD) optimization에 대해 알아보자.
SGD optimization은 weight(+bias)를 update하는 방법 중 하나로, 확률적으로 mini-batch를 뽑아 gradient descent를 진행하는 방법이다.
\( (\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \cfrac{\eta}{\lvert \mathcal{B} \rvert} \sum\limits_{i \in \mathcal{B}} \partial_{(\mathbf{w}, b)} l^{(i)}(\mathbf{w}, b) \)
- \(\leftarrow\)의 의미 : iterative(반복적) update
- \(\eta\) : learning rate
- \( \mathcal{B} \) : mini-batch
- \(\partial_{(\mathbf{w}, b)} l^{(i)} (\mathbf{w}, b)\) (\(= \nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\)) : gradient
먼저, gradient descent란, loss function의 최솟값에 다다르기 위해 gradient(경사) 방향으로 반복적으로 하강하는 방법이다.
모든 batch에 대해 gradient descent를 진행하는 batch gradient descent보다 mini-batch를 뽑는 경우 다음과 같은 이점이 있다.
- Memory의 resource를 아낄 수 있다.
- Non-convex optimization을 다룰 수 있다. 즉, local optima에 빠지는 문제를 해결할 수 있다.
- Mini-batch를 샘플링할 때마다 매번 조금씩 다른 그래프가 생성되기 때문이다.
최근댓글