자연어 처리 분야의 대세를 바꿔버린, 게다가 비젼 분야에도 응용되어 대세로 자리매김한 Transformer라는 아키텍쳐를 제안한 논문을 읽고 리뷰해보려 한다.
워낙 유명한 논문이어서 많은 리뷰가 존재하지만, 그만큼 논문 내용이 궁금해서 읽어보았다.
목차
Motivation
3D Vision 분야의 연구를 시작하기 앞서 여러 논문을 추천받아 읽어봤고, 몇 차례의 세미나를 통해 요즘 연구의 트렌드가 어떤지 1~2달간 알아보는 시간을 가졌다. (말하자면 연구 인턴?)
첫 번째 깨달은 점은 현재 연구 트렌드는 내가 전혀 알아들을 수도 없을 만큼 머신러닝, 딥러닝 기초 지식에 비해 깊어졌다는 것이다.
내가 배웠던 내용도 (2D object detection 분야를 예로 들자면) 2010년도 중반이 되어서야 인간의 수준을 막 넘기 시작했을 정도로 최근의 내용이었다고 생각했는데, 불과 7~8년도 되지 않는 시간 동안 내용이 너무 깊어졌음을 깨달았다. 하루빨리 따라잡기도 바쁜데, 2022 CVPR, ECCV 등의 논문들은 이해조차 불가능한 내용이 대다수였다.
두 번째 깨달은 점은 Transformer의 중요성이다.
Transformer가 뭔지도 몰랐는데, 지금의 트렌드는 vision 분야와 nlp 분야를 막론하고 transformer를 기반으로 하는 연구가 많다. 물론, 이것도 작년, 제작년 기준이고 현재에는 어떤 트렌드인지 정확하게는 모른다. 1~2년 전 논문 내용을 읽어보며 내 머릿속은 중간이 텅 비어있는 상태임을 깨닫고, survey 논문과 기본적인 논문들을 찾아보기 시작했기 때문이다. 그 기본적인 논문들 중 하나가 바로 이 transformer이다. 이 논문을 읽을 때에도 중간중간에 이해되지 않는 부분들이 너무 많아서, attention mechanism이 뭔지, embedding이 어떤 개념인지, encoder와 decoder가 정확히 어떻게 동작하는지 등 reference 논문을 새로 찾아 읽거나 같은 내용을 여러 차례 반복하면서 읽어봐야 했다.
그래도 기본기를 제대로 다진다는 마음으로 확실히 이해를 해보고 관련된 내용까지 포괄하는 리뷰를 진행해보려 한다.
Prerequisite
논문을 읽으면서 알아두어야 할 사전 지식을 간단히 정리하고 넘어갈 필요가 있다. RNN, CNN 등은 기초적이기도 하고, 설명할 내용이 많아 여기서 따로 다루지는 않을 것이다.
Deep Learning for Text and Sequences (일부)
말 그대로 Text(단어의 sequence, 글자의 sequence), time-serires data 등을 처리하는 deep learning 내용이다.
관련 용어들이 헷갈려서 옛날에 배운 내용을 복습해보면서 간단하게 정리해보려 한다.
Sequenctial data란, 개별적 요소(보통 words)가 순서를 갖고 나열되는 데이터를 말한다. 단어가 순서를 갖고 나열되면 문장이 될 것이다. 혹은 여러 image가 시간적 순서를 갖고 나열될 경우 video data가 될 것이다.
이러한 sequential data는 bag of words, one-hot vector 등으로 표현할 수 있다. 하지만 이들은 순서가 없어 다른 의미의 문장을 같은 형태로 표현하거나, 순서를 따지더라도 같은 의미인 문장이 다르게 표현될 수 있다.
Sequential data를 표현하기 위한 model을 설정할 때 고려할 사항은 다음과 같다.
- 길이가 가변적인 입력을 처리할 수 있어야 한다.
- Sequence 내 element의 순서를 처리할 수 있어야 한다.
- Long term dependency(sequence에 대해 앞서 나온 element가 뒤에 나온 element에 영향을 주는 경우)에 대해 적절한 처리를 해줄 수 있어야 한다.
- Sequence 간의 parameter를 공유해야 한다. (가변적인 sequence 처리에 필수적이다.) → 공통 parmeter로 처리한다.
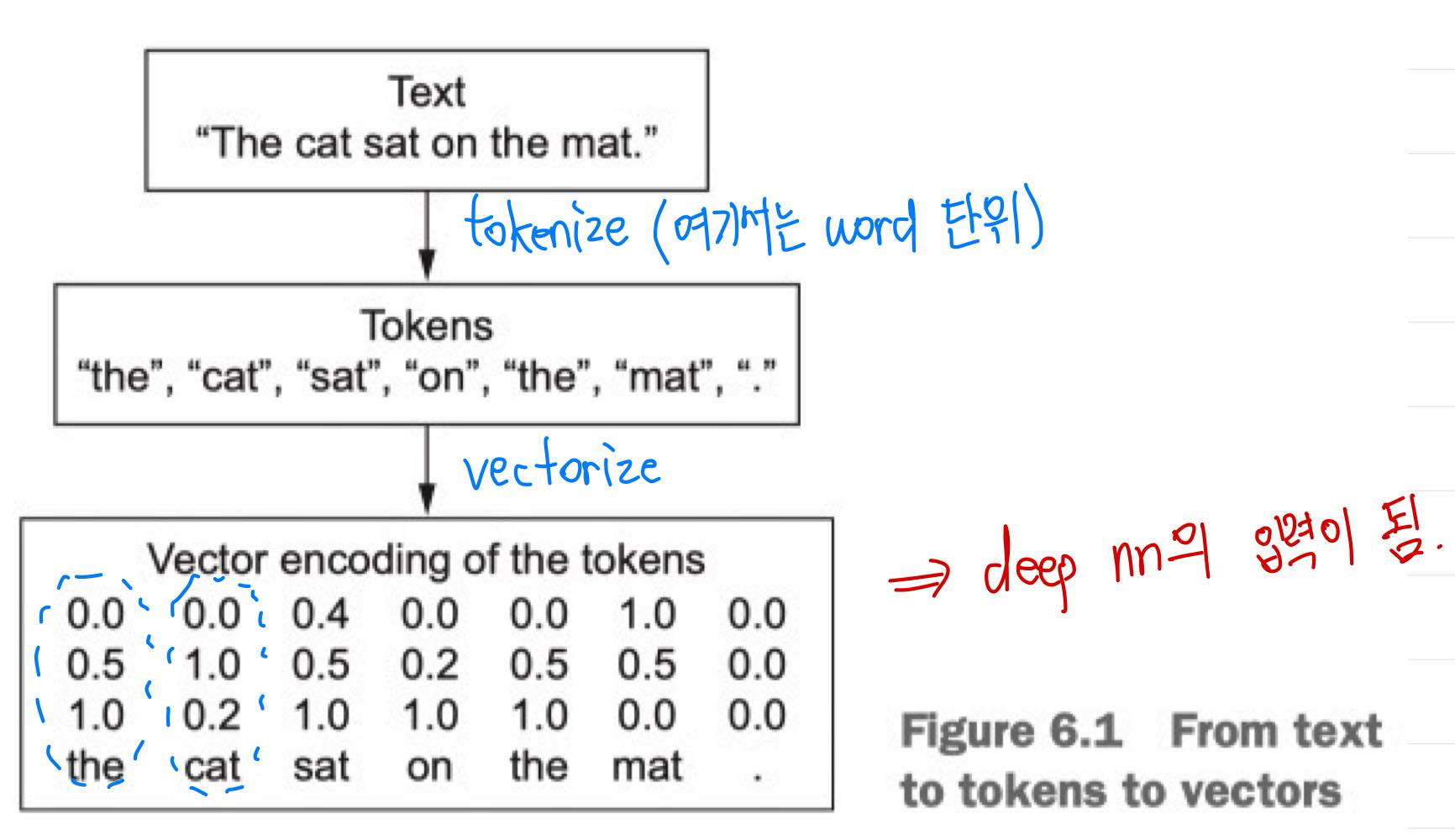
위 예시는 대표적인 sequential data인 text에서 words를 token으로 하여 tokenize와 vectorize를 한 예시이다.
Sequential data를 수치형 data(vector)로 나타내는 것을 tokenize라 하고, 쪼갠 단위(단어, 문자, 혹은 n-gram(단어의 묶음)등이 될 수 있음)를 token이라 한다.
이렇게 변환한 벡터들을 하나의 sequence tensor로 묶어 neural network의 입력으로 보내주게 되는데, 이렇게 묶는 것을 'token을 vectorize한다.'고 표현한다.
이렇게 vectorize하는 방법에는 대표적인 두 가지가 있다.
- One-hot encoding
- Token embedding
One-hot encoding을 자세히 다루지는 않겠다. 단순하고 쉽게 vectorize할 수 있지만, sparse하고, 고차원이므로 데이터를 표현하는 데 사용하는 용량이 커진다.
하지만 token embedding의 경우, 저차원이고, data로부터 학습이 가능하다.
Vectorize 결과 데이터가 embedding space에 놓이게 되는데(일반적으로 우리가 생각하는 2차원 좌표계의 벡터를 떠올려보자.), 이 공간 상에서 token 사이의 의미 관계를 기하학적 관계(direction, distance 등)로 나타낼 수 있다는 점이 특징이다.
참고로 data의 전처리는 'raw text → dictionary 생성 → 해당 token의 index로 data를 하나의 list로 표현'의 과정을 거친다.
Encoder and Decoder
다음은 Auto encoder의 과정을 나타낸 그림이다.
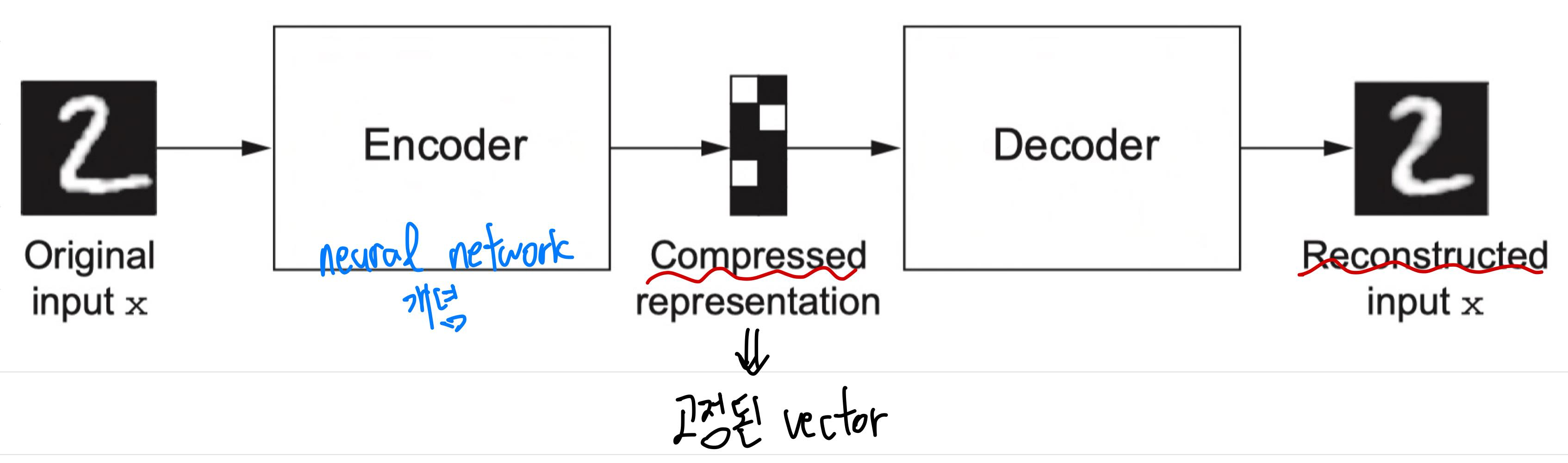
이와 같이, encoder는 어떤 데이터를 축약된 형태로 변환시키고, decoder는 축약된 형태의 vector를 입력으로 받아 원래 data를 복원하는 개념이다. 이 정도만 알아 두고 넘어가도록 하자.
Attention Mechanism
Transformer의 핵심이자, 여러 분야의 state-of-the-art 논문들에서 사용하는 방법이다.
이 부분은 attention을 처음 제안한 논문 'Neural Machine Translation by Jointly Learning to Align and Translate (by Dzmitry Bahdanau, KyungHyun Cho, Yoshua Bengio)'을 읽어보고, 요약한 내용이다.
당시 neural machine translation의 최근 모델은 encoder-decoder 모델을 사용한 경우가 많았다.
여기서 encoder는 source sentence를 입력으로 받아 neural network를 거쳐 fixed-length (context) vector를 출력했고, decoder는 이 벡터로부터 translation 결과를 출력했다.
그런데, 문제는 neural network가 긴 문장(특히 학습 도중의 corpus(말 뭉치)보다 긴 문장)을 다루기가 어렵다는 점이다.
따라서 논문에서는 encoder-decoder 구조의 모델을 확장하여 align과 translate를 연결시켜 학습하는 모델을 제안했다.
- 모델이 word를 출력할 때마다 source sentence 내에서 관련된 정보가 집중된 특정 위치를 찾는다.
- 찾은 위치와 관련된 context vector와 이전에 만든 target word들을 기반으로 target word를 예측한다.
좀 더 자세하게 살펴보기 전에, 몇 가지 알아두어야 할 부분이 있다.
RNN Encoder-Decoder
RNN Encoder-Decoder 아키텍쳐는 align과 translate를 동시에 학습하는 아키텍쳐이다.
인코더는 input sentence에 해당하는 벡터의 시퀀스 \( \mathbf{x} = \left( x_1, \cdots, x_{T_x} \right) \)를 vector \(c\)로 encoding한다.
RNN은 다음과 같이 활용된다.
\( h_t = f(x_t, h_{t-1}) \)
\( c = q(\{h_1, \cdots, h_{T_x} \} ) \)
여기서 \(h_t \in \mathbb{R}^n\)는 position \(t\)에서의 hidden state, \(c\)는 해당 hidden state의 sequence로부터 얻은 vector이고, \(f\)와 \(q\)는 nonlinear function이다.
디코더는 이전에 예측된 words \( \{ y_1, \cdots, y_{t'-1} \} \)와 context vector \(c\)가 주어졌을 때, 다음 word \(y_{t'}\)을 예측하도록 학습된다. 수식으로 표현하면 다음과 같다.
\( p(\mathbf{y}) = \prod\limits_{t=1}^T p(y_t \vert \{ y_1, \cdots, y_{t-1} \}, c) \)
여기서 \( \mathbf{y} = (y_1, \cdots, y_{T_y})\)이다.
RNN에서 각 조건부 확률은 다음과 같이 모델링할 수 있다.
\( p(y_t \vert \{y_1, \cdots, y_{t-1} \}, c) = g(y_{t-1}, s_t, c) \)
\(g\)는 nonlinear function이고, multi-layer로 이루어져 있다. \(s_t\)가 RNN의 hidden state이고 word, 즉 \(y_t\)의 확률을 출력하는 함수이다.
위 내용에 따라 attention mechanism을 제대로 이해해보자.
Attention에서는 인코더로 bidirectional RNN을 사용하고, 디코더는 searching의 역할을 한다.
Attention mechanism의 핵심: Encoder-Decoder 구조
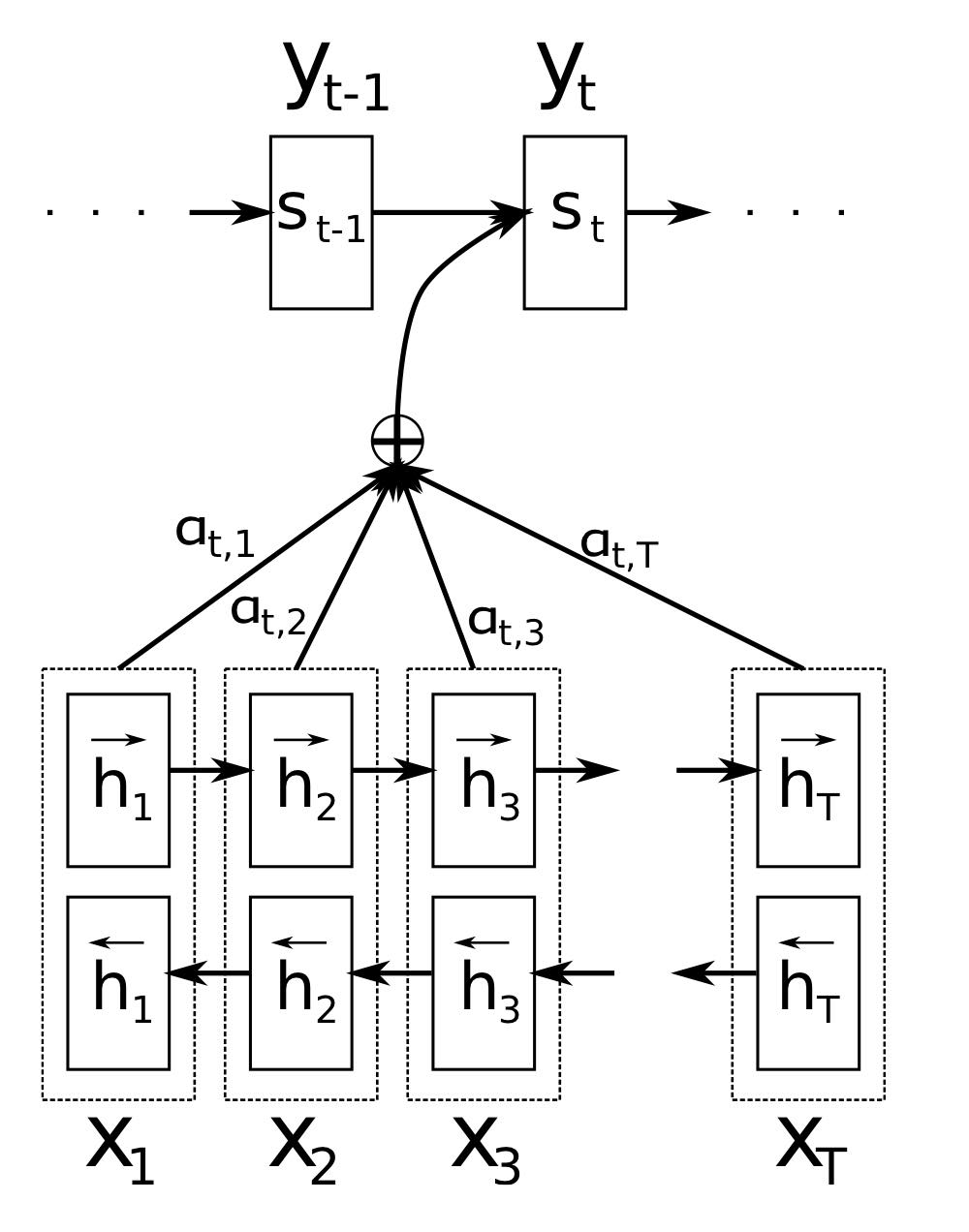
위 사진은 attention mechanism을 그림으로 나타낸 것이다. Source sentence \(\mathbf{x}\)가 주어졌을 때 t번째 target word \(y_t\)를 얻기 위한 과정으로, 각 구성요소에 대한 설명은 다음과 같다.
- Encoder에서 source sentence \(\mathbf{x}\)로부터 forward hidden states \(( \overrightarrow{h}_1, \cdots, \overrightarrow{h}_T ) \)와 backward hidden states \( ( \overleftarrow{h}_1, \cdots, \overleftarrow{h}_T )\), 최종적으로 annotation \(h\) (즉, encoder에서의 hidden state)를 얻는다.
- Decoder에서 이러한 annotation들을 weigted sum 한 값(encoder에서 출력한 모든 정보를 포함함)과 이전 hidden state \(s_{t-1}\)을 고려하여 \(s_t\)를 얻어낸다.
- 아래의 상세 설명에서 \(i\)는 디코더가 처리중인 time step에 대한 index, \(j\)는 annotation, 즉 인코더의 출력에 대한 index이다.
Encoder에 대해 먼저 상세하게 알아보자.
앞서 언급한 일반적인 RNN 식은 \( h_t = f(x_t, h_{t-1})\)로, \(x_1\)부터 \(x_{T_x}\)까지의 input sequence \(\mathbf{x}\)를 받는다.
하지만 attention에서는 이전 단어 뿐만 아니라 뒤에 올 단어들까지 summarize한 annotation을 얻기 위해 bidirectional RNN(BiRNN)을 인코더로 사용한다.
BiRNN은 forward RNN과 backward RNN으로 구성된다.
- Forward RNN ( \(\overrightarrow{f}\) )
- \(x_1\)부터 \(x_{T_x}\) 순서인 input sequence를 읽어와 forward hidden states의 sequence인 \((\overrightarrow{h}_1, \cdots, \overrightarrow{h}_{T_x})\)를 계산한다.
- Backward RNN ( \(\overleftarrow{f}\) )
- 역순, 즉 \(x_{T_x}\)부터 \(x_1\)의 순서인 sequence를 읽어와 backward hidden states의 sequence인 \((\overleftarrow{h}_1, \cdots, \overleftarrow{h}_{T_x})\)를 얻는다.
그 후, forward hidden state \(\overrightarrow{h_j}\)와 \(\overleftarrow{h_j}\)를 연결하여 각 단어 \(x_j\)에 대한 annotation을 얻는다. 따라서 annotation은 다음과 같은 형태가 된다.
\(h_j = \left[ \overrightarrow{h}^{\top}_{j} ; \overleftarrow{h}^{\top}_{j} \right]^\top \)
이에 따라 \(h_j\)는 이전 단어들과 이후 단어들에 대한 정보를 둘 다 포함하게 된다.
RNN은 현재 input을 더 잘 표현하는 경향이 있는데, 이로 인해 \(h_j\)는 \(x_j\) 주변 단어들을 더 잘 표현할 것이다. 이러한 annotation은 decoder와 alignment model에서 context vector를 계산하는 데 쓰이게 된다.
다음으로, decoder를 자세히 알아보자.
새로운 아키텍쳐에서는 조건부 확률을 다음과 같이 나타낸다.
\( p(y_i \vert y_1, \dots, y_{i-1}, \mathbf{x}) = g(y_{i-1}, s_i, c_i) \)
여기서 \(s_i\)는 RNN의 hidden state이며, 이전 state, 이전 word, 현재 context vector를 통해 다음과 같이 계산된다.
\( s_i = f(s_{i-1}, y_{i-1}, c_i) \)
기존 encoder-decoder 모델의 식과 비교해보면, fixed-length vector인 \(c\) 대신 time step마다 다른 \(c_i\)를 사용하는 것을 볼 수 있다.
여기서 context vector \(c_i\)는 annotation의 sequence인 \( (h_1, \cdots, h_{T_x} ) \)에 의해 결정된다. 이때 annotation \(h_i\)는 input sequence 전체에 대한 정보를 갖는데, 특히 i번째 단어 주변 부분에 대한 정보를 집중적으로 갖는다.
그 후, context vector는 다음과 같이 annotation들의 wegithed sum으로 얻는다.
\( c_i = \sum\limits_{j=1}^{T_x} \alpha_{ij} h_j \)
이러한 weighted sum 계산 과정을 잘 살펴보자. \(\alpha_{ij}\)를 '\(x_j\)에서 \(y_i\)로 번역될 확률', 또는 '\(y_i\)가 \(x_j\)로 align될 확률'로 생각해보면, i번째 context vector \(c_i\)를 전체 annotation에 대한 expected annotation으로 생각할 수 있다.
여기서 weight \(\alpha\)는 다음과 같이 계산한다.
\( \alpha_{ij} = \cfrac{\text{exp} (e_{ij}) }{\sum\limits_{k=1}^{T_x} \text{exp}(e_{ik}) } \)
\( e_{ij} = a(s_{i-1}, h_j) \)
\(e\)는 energy로, input이 (annotation의)위치 \(j\) 얼마나 주변에 있는지, output이 time step \(i\)에 얼마나 맞는지에 대한 점수이다. 즉, 이전 hidden state \(s_{i-1}\)에 대해 annotation \(h_j\)가 얼마나 얼마나 중요한지를 나타낸다.
따라서 디코더의 이전 hidden state(출력값)이 annotation \(h_j\)와 비슷할수록 energy 값이 커지는 것이다.
RNN의 이전 hidden state와 input sentence의 j번째 annotation을 입력으로 받아 alignment model \(a\)를 거쳐 구한다. \(a\)는 feedforward neural network로 parameterize하여 함께 training시킨다.
기존 모델과 달리 이러한 alignment를 latent variable(직접적으로 관찰되거나 보이지 않는 변수)로 보지 않고 soft alignment를 직접 계산하여 cost function의 gradient가 역전파되도록 했다. 즉, 학습 과정에서 alignment model과 전체 translation model을 연결시켜 학습을 진행했다.
weight인 \(\alpha\)는 energy에 softmax 함수를 취하여 확률적인 값을 나타내게 된다. 즉, 전체 annotation 중에서 해당 annotation의 energy 값의 비율이 얼마나 되는지를 나타낸다.
이렇게 구한 weight와 \(h_j\)를 weighted sum 한다는 것(\(c_i\)의 계산)은, time step \(i\)에서 각 annotation \(h_j\)와 그 annotation이 중요한 비율 \(\alpha_{ij}\)를 곱한 값들을 모든 \(j\)에 대해 구하는 것이다.
이에 따라 decoder는 매번 hidden state \(s\)를 출력할 때마다 모든 annotation 정보(encoder에서 출력한 hidden state 정보)를 사용할 수 있게 된다.
Energy \(e_ij\) 부분이 decoder에서의 attention mechanism을 수행한다. 디코더는 source sentence 중에서 주의를 기울일 부분(parts to pay attention to)을 결정한다.
이에 따라 인코더는 source sentence 전체 정보를 encoding할 필요가 없어지며, annotation 시퀀스 전체에 정보를 전달하고, 디코더는 그 정보를 선택적으로 되찾게 된다.
Attention 내용은 현재도 계속해서 응용되어 CV 분야, NLP 분야에서 사용하고 있으므로 정확하게 알아둘 필요가 있다.
Introduction
NLP, 특히 Machine Translation 분야에서 이전까지는 encoder와 decoder 구조를 포함하는 RNN, CNN 기반의 연구가 대부분이었다. Attention mechanism이 나온 뒤로는 attention을 조금 추가한 정도에 그쳤다.
하지만 이 논문에서는 완전히 attention mechanism만 recurrence와 convolution에 적용한 Transformer라는 아키텍쳐를 제안하였다.
Recurrent Model의 한계점
Recurrent model은 input과 output sequence의 symbol position을 계산한다.
계산 시 step에 position을 align함으로써 hidden state의 sequence \(h_t\)를 만드는데, 이때 hidden state \(h_{t-1}\)과 position \(t\)의 입력의 함수로 사용한다.
이러한 방식때문에 recurrent model은 본질적으로 학습을 parallelization할 수 없다. 즉, 긴 sequence length를 다룰 수 없는 한계가 존재한다.
Factorization trick, conditional computation 등으로 계산 효율성을 높이고, 이에 따라 모델 성능도 높이는 연구가 많이 진행됐지만, 여전히 sequential computation의 제약이 존재했다.
Attention
따라서 Transformer에서는 recurrence model을 사용하지 않고 전적으로 attention 메커니즘만을 사용한다.
위에서도 언급했듯이, attention을 사용하면 input 및 output sequence의 길이에 상관 없이 dependency를 모델링할 수 있다.
이를 통해 Transformer는 병렬 계산이 가능하여 학습 속도가 빠르고, translation 성능 또한 매우 좋아졌다.
특히 Transformer에서는 self-attention이 사용된다.
Self-attention(a.k.a. intra-attention)은 같은 sequence 내에서 서로 다른 position(요소)들 간에 attention mechanism을 적용하는 방법이다.
다음 포스팅에서 이어서 Transformer에 대한 본격적인 내용을 다뤄볼 것이다.








최근댓글