Ref. 자료구조 기초 (Feat. 생활코딩, 동빈나)

알고리즘을 배우기 앞서서, 생활코딩을 참고하여 간단하게 자료구조의 이론에 대해 알아보려 한다.

자료구조 분류 정리

 

 

목차

 

 

 

 

 

 

 

 

0. 자료구조 개요

 

 

 

 

1) 자료구조란?

 

자료구조 (Data Structure) : 데이터를 표현하고, 관리하고, 처리하기 위한 구조

→ 알고리즘을 구현할 시에 각각의 자료구조가 갖는 장점과 한계를 숙지한 후에, 적재적소에 잘 활용하는 능력 필요

 

 

 

 

2) 자료구조를 학습하는 목적

 

메모리를 효율적으로 사용하기 위해서!

 

컴퓨터는 기본적으로 CPU, 메모리, 스토리지 3가지 주요 부품으로 이루어짐

• CPU : 중앙정보처리장치, 레지스터, 데이터를 연산 or 처리하는 가장 중요한 부분, 매우 빠름
• 메모리 : RAM(Random Access Memory), CPU에서 직접 접근 가능, 사용자가 자유롭게 내용을 읽고 쓸 수 있음, 휘발성 기억장치, 빠름
• 스토리지 : HDD, SSD, 비휘발성 기억장치, 용량이 매우 크지만 느림

 

데이터는 보통 스토리지에 저장되는데, 매우 느리기 때문에 CPU와 함께 일하기에는 부족함

→ 어떤 프로그램을 실행하면 해당 프로그램과 데이터는 메모리로 옮겨짐

 

CPU는 메모리에 로드된 데이터를 이용하여 일을 하기 시작!

∴ 실행속도를 결정하는 주요한 장치가 메모리이며, 자료구조는 이러한 메모리를 효율적으로 사용하기 위해 배움

 

 

 

3) 자료구조와 알고리즘의 관계

 

자료구조를 구현하기 위해서 알고리즘이 필요함

 

• 자료구조의 알고리즘 : 데이터를 저장 및 탐색하는 방법
• 자료구조를 이용한 알고리즘 : 자료구조를 활용해 문제를 해결하는 과정

 

 

 

 

4) 자료구조의 구성

 

• Insert : 데이터를 어떻게 저장할 것인가?
• Search : 데이터를 어떻게 탐색할 것인가?
• Delete : 데이터를 어떻게 삭제할 것인가?

 

 

자료구조 분류 정리

 

• 단순 구조 : 프로그래밍 시 사용되는 기본 Data Type
• 선형 구조 : 저장되는 자료의 전후 관계가 1:1 (List, Stack, Queue ...)
• 비선형 구조 : 데이터 항목 간의 관계가 1:n or n:m (Tree, Graph ...)
• 파일 구조 : 서로 관련된 필드들로 구성된 레코드의 집합인 파일에 대한 자료구조

 

→ Data Structure는 언어마다 다름

→ Data Structure 각각의 주요 개념들을 파악해야 함

 

 

 

 

1. Array(배열)

 

배열 : 많은 데이터를 하나의 이름으로 Grouping해서 관리하기 위한 Data Structure

 

배열의 구조

• Index : Group 내의 순서대로 번호를 부여한 것 (색인)
• Element : Group을 형성하는 요소들
• Value : 각 요소가 나타내는 값

배열의 구조

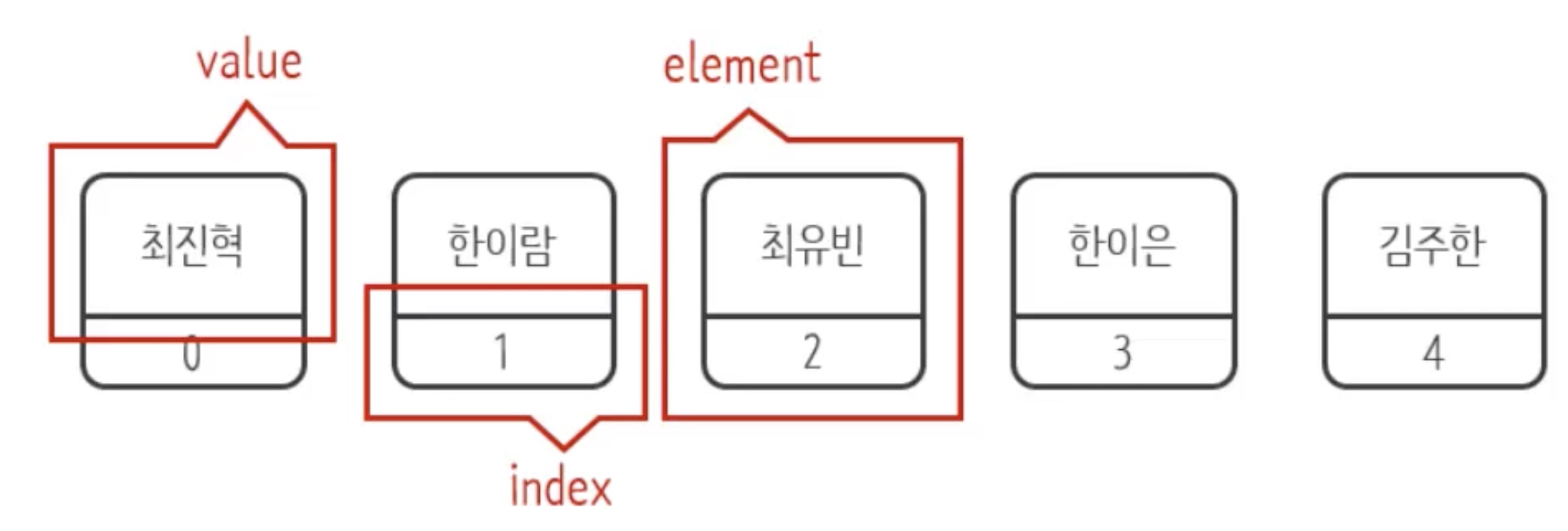
→ 배열, 반복문을 함께 사용하여 배열 각각의 값들을 다루고 접근할 수 있음

 

 

 

 

 

2. List

 

 

 

1) List의 특징

 

1. Data가 순서대로 저장됨
2. 중복 저장을 허용함

 

 

 

 

2) Array vs List

 

→ 비슷하지만 일반적인 사용 방법에 있어서 차이점이 존재

Array vs List

 

Array는 Index가 중요(Index를 통해 데이터에 접근)하지만, List는 순서가 매우 중요

 

 

(1) Data를 추가할 때

 

4 번째(index : 3) 값에 50을 입력한다면

 

• 배열에서 값을 추가할 때에는 '3'이라는 index를 통해 40이라는 값을 40으로 덮어쓰는 것
• 리스트에서는 40이라는 데이터를 뒤로 한 번 미루고, 50이라는 값을 index 3으로 추가함

 

 

 

(2) Data를 삭제할 때

 

4 번째(index : 3) 값을 삭제한다면

 

• 배열에서 값을 삭제하면 해당 index가 비게 됨 (메모리는 그대로 차지)
• 리스트에서 값을 삭제하면 뒤에 있던 index가 앞으로 당겨짐

 

→ 배열의 장점 : index에 따른 값이 변하지 않으므로, index를 통한 데이터의 접근이 용이함

→ List의 장점 : 데이터가 연속적이므로 데이터가 있는지 없는지 확인할 필요가 없음

→ List에서의 index는 단순히 몇 번째 데이터인가에 대한 정보를 갖지만, Array에서는 그 값을 지칭하는 유일무이한, 변하지 않는 정보임

 

 

 

 

3) List의 기능(Operation) (중요!)

 

 

 

(1) 처음, 끝, 중간에 element를 추가 또는 삭제하는 기능

 

 

 

(2) List에 데이터가 있는지 체크하는 기능

 

→ 대부분의 Data Structure에서 공통적으로 지원하는 기능 

 

 

(3) List의 모든 데이터에 접근할 수 있는 기능

 

 

 

(4) 언어별 비교 (C, JavaScript, Python, Java)

 

1. C : 리스트를 지원하지 않음

→ 직접 구현하거나 다른 사람이 구현한 라이브러리를 사용해야 함 (∴리스트에 대한 이해가 더 중요!)

 

 

2. JavaScript : C family language이지만, 리스트 기능을 가짐

→ 배열이 곧 리스트

→ 'splice' 메서드를 통해 리스트 제어 

ex)

numbers = [10, 20, 30, 40, 50];

number.splice(3, 1); // index 값이 3인 데이터부터 1개의 data

for(i = 0; i < numbers.length; i++) {
	console.log(numbers[i]);
}

 

 

3. Python : 배열 대신에 기본적으로 리스트를 제공함

→ 리스트가 곧 배열

ex)

numbers = [10, 20, 30, 40, 50]

numbers.pop(3) // index 3인 값(40)을 제거함 → 자동으로 50이 index 3이 됨
print(numbers[0]) // 배열처럼 사용 가능

for number in numbers:
	print(number)

 

 

4. Java :  배열과 리스트가 서로 완전히 다른 문법!

→ 배열과 리스트를 모두 지원함

→ 특히, Linked List와 Array List 모두를 지원함

ex) 

int[] numbers = {10, 20, 30, 40, 50}; // 배열의 datatype이 int인 numbers라는 배열

ArrayList numbers = new ArrayList(); // ArrayList라는 객체를 만들어서 리스트 생성
numbers.add(10);
numbers.add(20);
numbers.add(30);
numbers.add(40);
numbers.add(50);
numbesr.remove(3); // Python의 pop(3)과 같은 역할

 

• LinkedList와 ArrayList

LinkedList numbers = new LinkedList();
ArrayList numbers = new ArrayList();

	추가/삭제	인덱스 조회
ArrayList	느림	빠름
LinkedList	빠름	느림

 

 

 

 

 

4) Array List (순차 리스트)

 

• 장점 : Data를 가져올 때 빠름 (Index 값으로 data를 가져올 때 빠름)
• 단점 : Data를 추가 또는 삭제할 때 느림 (Index를 하나씩 변경해 주어야 함)

 

(1) Array List의 동작 - Data 추가/삭제

 

 

만약 'index 1'에 50이라는 값을 대입하고 싶다면?

→ 40 값을 index 4로, 30 값을 index 3으로, 20 값을 index 2로 한 칸씩 밀어내어 빈 공간을 만든 후 50 값 추가

50이 index 1에 추가된 결과

 

만약 'index 2'의 30이라는 값을 삭제하고 싶다면?

→ 30을 삭제시킨 후, 40 값을 index 2로 당겨 빈틈을 없앰

30을 없앤 결과

 

 

 

 

(2) Array List의 동작 - Data 조회

 

내부적으로 배열을 사용하며(해당 index의 주소가 저장되어 있음), data가 수정되어도 size 값도 같이 수정되기 때문에 Index로 값을 가져오기 쉬움

 

 

 

 

5) Linked List (연결 리스트)

 

→ 일반적으로 Array List보다 Linked List가 구현하기 더 어려움

 

※ 사전 지식

• RAM(Random Access Memory) 의 특징 : Data가 어디에 위치하는가, 즉 Data의 address를 알 때 매우 빨리 데이터에 접근할 수 있음
• Array List vs Array List

Array List와 Linked List의 메모리 상에서의 차이점

• 메모리 사용 방식의 차이점
  • ArrayList : 같은 element들이 메모리 상에 연속적으로 붙어 있음
  • LinkedList : 각 data(element)들이 흩어져 있지만, 서로 연결되어 있음

 

→ 서로 연결되어 있기 때문에, Linked List에서는 element보다 'node, vertex'라는 표현을 많이 사용함

Linked List Example

• node(마디, 교점), vertex(정점, 꼭지점) : '연결'과 연관된 구조를 설명하기 위해 이와 같은 표현을 함 (예시에서 4개의 노드 존재)
  • node의 표현 : C에서는 '구조체', 객체지향 프로그래밍 언어에서는 '객체'를 사용하여 표현
• node 내에는 두 개의 'field'가 존재
  • Data Field : '값'을 저장
  • Link Field : '다음 element(node)'를 나타내 주는 변수
• HEAD : Linked List는 연결되어 있기 때문에, 첫 번째 node를 알아야 함 → Head Field라는 변수를 통해 첫 번째 노드에 대한 데이터를 저장함

 

 

 

(1) Linked List의 동작 - Data 추가/삭제

 

 Link 관계만 바꿔주면 되므로 Data를 추가, 삭제하는 과정이 매우 빠름 (Array List는 연관된 모든 index를 바꿔줘야 했음)

 

• Data를 처음 위치에 추가

→ pseudo code

// 1. node 생성 (Vertex 개체를 만듦)
Vertex temp = new Vertex(85) // '85(input)'라는 node를 temp라는 이름으로 생성 (Vertex 객체를 만듦)

// 2. 'next'라는 메서드를 통해 link를 변경해줌
temp.next = head
// List의 head를 85를 저장한 temp node 다음으로 지정
// '15'라는 노드의 reference가 바로 head에 저장되어 있음

// 3. 15를 가리키던 head가 85를 가리키도록 변경
head = temp // 15를 가리키고 있던 head를 85를 가리키도록 변경함

Data 처음 위치에 추가

 

• Data를 중간에 추가

→ pseudo code

// 전체적인 개념 : 추가할 위치 앞 노드의 reference는 temp1, 뒷 노드의 reference는 temp2

Vertex temp1 = head // 첫 번째 노드의 reference (head)를 temp1(임시 변수)에 담음

// k : 삽입할 index (2)
while (--k != 0) // k가 2 → 1 → 0이 되며, --k임에 유의
	temp1 = temp1.next

// temp1 : 15의 reference → (k=1) 6의 reference → (k=0이므로 while문 끝)
// 즉 while문을 끝내면 temp1은 6을 가리킴


Vertex temp2 = temp1.next // temp2는 6 뒤인 23을 가리킴

Vertex newVertex = new Vertex(input) // 새로운 node (값:90) 생성

temp1.next = newVertex // temp1이 새로운 node, 즉 90을 가리킴

newVertex.next = temp2 // 새로운 node가 23을 가리킴

Data를 중간에 추가

 

• Data 삭제

→ pseudo code

Vertex cur = head

// 삭제할 node를 찾는 과정
while (--k != 0)
	cur = cur.next
// k : 2 → 1 → 0
// cur : 15를 가리킴 → (k=1) 6을 가리킴 → k=0이므로 while문 끝
// 즉 'cur'은 삭제할 node 이전의 값을 가리킴

Vertex tobedeleted = cur.next // 삭제할 node(19)를 가리키는 'tobedeleted' 변수 생성
// 주목 : 바로 삭제하지 않고, 링크 관계를 변경시켜주기 위해 'tobedeleted' 변수를 생성하는 과정을 거침

cur.next = cur.next.next // '6'값을 갖는 node가 90이 아닌 23을 가리키도록 Link를 변경시킴
// 이 line이 생성된 이후에는 '6'node, '90'node 모두 '23'node를 가리킴

delete tobedeleted // 90 node 제거

Data 삭제

 

 

 

(2) Linked List의 동작 - Data 조회

 

→ 조회를 위해서는 head, 즉 처음 node부터 차례로 찾아야하므로, 조회의 시간이 오래걸림

 

'4'라는 값을 갖는 node를 찾고 싶다면

1. head를 통해 첫 번째 node ('15' node)를 찾음, 4인지 확인
2. 다음 node('6' node)를 찾음, 4인지 확인
3. 다음 node('23' node)를 찾음, 4인지 확인
4. 다음 node('4' node)를 찾음, 4인지 확인 → 4 찾음, node return!

 

'index 3 (4번째 노드)'의 값을 찾고 싶다면

1. head를 통해 첫 번째 node 찾음, count = 0
2. next, count = 1
3. next, count = 2
4. next, count = 3 → 'index 3' 찾음, node return!

 

 

 

 

6) Doubly Linked List (이중 연결 리스트)

 

Doubly Linked List 구조

→ Linked List에서 'Previous Field'를 추가하여 이전 node를 가리킬 수 있도록 한 Linked List

→ 일반적으로 가장 많이 사용하는 Linked List

 

• 장점
  • 조회 시 index를 뒤에서부터 '이전으로' 거쳐서 가져올 수 있음 → 조회하는 node의 index가 전체 size의 반보다 클 때 단순 연결 리스트보다 빠르게 조회 가능 (조회가 느린 연결 리스트의 단점을 보완)
  • next 메소드 뿐만 아니라 previous 메소드도 지원!
• 단점
  • 메모리를 더 많이 사용하며, 구현이 좀 더 복잡해짐

 

※ 동작은 다른 자료 참조!

 

 

 

 

 

3. 스택(Stack), 큐(Queue), 덱(Deque)

 

→ 스택과 큐는 컴퓨터 공학에서 가장 기본이 되는 자료구조

→ 스택 : 택배 상하차 (위에 쌓고, 위에서 꺼냄)

→ 큐 : 은행 창구 (번호표를 뽑고 먼저 온 사람이 먼저 서비스를 받음)

 

 

 

 

1) Stack

 

LIFO(Last In First Out) 구조

→ 스택은 입구, 출구가 하나밖에 없는 상태로 표현할 수 있음

• 'C++의 <stack>'  라이브러리에서
  • Push : 삽입 메소드
  • Pop : 삭제 메소드
  • top : 스택의 가장 위에 있는 element반환

 

• Stack Underflow : 자료가 없을 때 삭제하려는 경우의 오류
• Stack Overflow : 스택 이상의 크기를 갖는 자료를 삽입하려 할 경우의 오류

 

• 장점 : 데이터의 삽입과 삭제가 빠름 (맨 위의 원소에만 접근하면 됨) →  중간 원소를 삽입/삭제/탐색하는 것은 stack의 목적에 맞지 않음
• 단점: 탐색을 하려면 원소를 하나하나 꺼내고 옮겨서 해야 함 (맨 위의 원소에만 접근 가능)

 

• Application : 재귀 알고리즘에서 많이 사용, 역추적을 할 경우 많이 사용(ex. 문서 작업의 실행 취소)
  • ex) 괄호 검사, 역순 문자열 만들기, 후위 표기법으로의 변환

 

 

 

2) Queue

 

FIFO(First In First Out) 구조 : 먼저 넣은 데이터가 먼저 나감

Queue에서의 원소 삽입

Queue에서의 원소 삭제

• 'C++의 <queue>' 라이브러리에서
  • push : 삽입 (Enqueue)
  • pop : 삭제 (Dequeue)
  • front : 가장 먼저 들어온(가장 앞 줄의) element 반환
  • back : 가장 늦게 들어온(가장 뒷 줄의) element 반환

 

• 장점 : 데이터의 삽입/삭제가 빠름
• 단점 : 중간에 위치한 데이터로의 접근이 어려움

 

※ 배열로 구현할 시

• 선형 큐
  • Front는 고정, Back을 이동하면서 데이터를 삭제하는 경우, 데이터를 제거할 시 나머지 데이터를 한 칸씩 모두 옮겨야 함
  • 둘 다 이동하면서 삽입/삭제할 경우, 배열의 끝에 저장되어 있는 상항이 되면 Back을 더 이상 이동시킬 수 없어 overflow 발생
• 순환 큐 : 선형 큐를 보완하기 위해 front가 큐의 끝에 닿으면 큐의 맨 앞으로 자료를 보내 원형으로 연결함

 

• Application : 데이터를 입력된 순서대로 처리할 경우, BFS(너비 우선 탐색) 구현
  • 우선순위 Queue : 우선순위를 가진 항목들을 저장하는 큐 
  • ex) BFS, 콜센터 대기 순서, 프로세스 관리 ...

 

 

 

(1) Priority Queue (우선순위 큐)

 

→ 입력 순서와 상관없이 우선순위가 높은 데이터가 가장 먼저 처리됨

→ 새로운 노드를 삽입하면 우선순위에 맞는 위치에 삽입 (Enqueue)

→ 제거할 때에는 우선순위가 가장 높은 노드를 삭제 (Dequeue)

 

 

 

 

3) Deque

 

→ queue와 비슷하지만, queue는 front에서 삭제 / rear에서 삽입만 가능하지만, 덱의 경우 front와 rear에서 삽입, 삭제가 모두 가능

→ 연속적인 메모리를 기반으로 하는 'Sequence Container' (임의 접근 반복자 제공)

→ 크기가 가변적임

→ 중간 요소가 삽입 또는 삭제될 때, 요소들을 앞/뒤로 밀 수 있음 (vector보다 좋은 성능을 가짐, 하지만 front/rear에서의 삽입/삭제 성능은 좋지만 중간에서는 좋지 않음)

 

• 장점
  • 데이터의 삽입, 삭제가 빠름
  • 크기가 가변적
  • 앞, 뒤 모두에서 삽입/삭제 가능
  • index로 임의 원소 접근 가능
  • 새로운 원소 삽입 시 메모리를 재할당하고 복사하지 않고, 새로운 단위의 메모리 블록을 할당하여 삽입함
• 단점
  • deque의 중간에서의 삽입/삭제가 어려움
  • 구현이 어려움

 

• Application
  • front/rear에서의 삽입/삭제가 자주 일어나는 경우
  • 데이터 개수가 가변적일 경우
  • 데이터 검색을 거의 하지 않는 경우 (element 접근을 랜덤하게 할 때)

 

 

 

 

 

4. Graph(그래프), Tree(트리)

 

 

 

1) Graph

 

→ 노드(node, or vertex), 노드를 연결하는 간선(edge)으로 구성됨

Undirected Graph

 

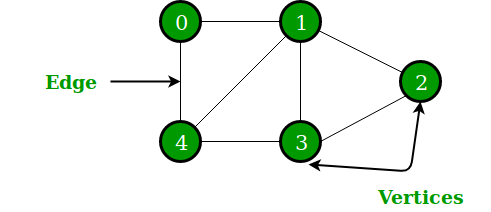
→ Undirected, Directed로 나뉨

 

 

(1) Terminology

 

• 진입 차수(In-degree, 내차수) : 방향 그래프(Directed Graph)에서 외부 노드에서 오는 간선(Edge)의 수
• 진출 차수(Out-degree, 외차수) : 외부 노드로 나가는 간선의 수
• 차수(Degree) : In-degree + Out-degree
• 트리와 달리 Graph의 노드는 한 개 이상의 In-degree를 가질 수 있음
• 완전 그래프 : 모든 노드가 간선으로 연결된 그래프
• 부분 그래프 : 그래프의 부분집합

 

• Application : 지하철 노선도, 지도 어플의 최단 경로, Facebook Follower

 

 

 

(2) 구현 방식에 따른 분류 - 인접 행렬 방식 & 인접 리스트 방식

 

 

• 인접 행렬 방식 (Adjacency Matrix)

→ 공간을 많이 차지하지만 간단함

→ 노드의 제곱에 해당하는 공간 차지

 

• 인접 리스트 방식 (Adjacency List)

→ 각각의 노드에 인접한 노드 리스트를 입력하는 방법 (일반적인 방법)

→ 연결 리스트 방식은 공간이 적게 들고 노드를 새로 추가하기 쉽지만 구현이 복잡함

 

 

2) Tree

 

→ 계층 구조를 갖고 있는 자료구조

→ 주 목적 : 탐색

 

 

 

(1) Terminology

 

Tree의 구조

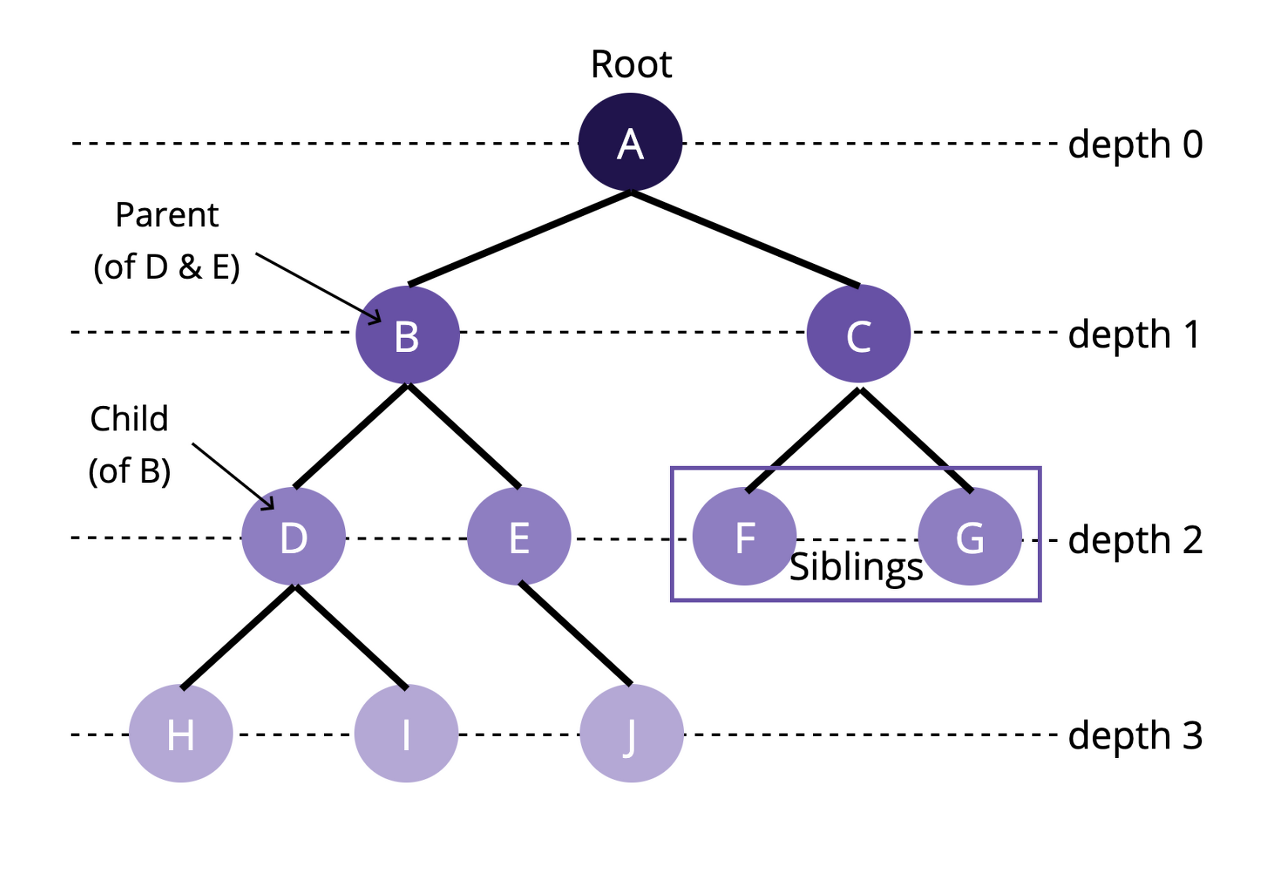
• Root : 최상위 노드 (depth = 0)
• Edge : 노드와 노드를 잇는 선
• Leaf : 자식이 없는 노드
• Depth : 루트를 기준으로 다른 노드로 접근하기 위한 거리
• Height : 한 노드를 기준으로 Leaf노드까지의 최대 깊이

 

• ex) DOM, Dictionary, File System

 

 

 

(2) Binary Search Tree (BST, 이진 탐색 트리)

 

Binary Search Tree

→ 최대 2개의 자식 노드만 갖는 Tree

→ 왼쪽 자식 노드는 작은 값, 오른쪽 자식 노드는 같거나 큰 값이 들어감

→ 이진 탐색 트리를 순회하는 두 가지 대표적인 방법 : 깊이 우선 탐색 (Depth First Search, DFS), 너비 우선 탐색 (Breadth First Search) 알고리즘

→ BST의 종류

• 정 이진 트리 (Full Binary Tree)
• 완전 이진 트리 (Completed Binary Tree) : 노드가 위에서 아래로, 왼쪽에서 오른쪽으로 채워지며, 잎 노드 두개의 level 차이가 1 이하 → heap 구현에서의 기본

 

• 포화 이진 트리 (Perfect Binary Tree)

 

 

 

(3) Heap

 

→ 힙은 완전 이진 트리 (Complete Binary Tree)를 기본으로 한 자료구조

→ 일반적으로 배열을 사용하여 구현

→ 최댓값 및 최솟값을 빠르게 찾아내기 위해 고안됨

→ 힙 속성 (property)

• A가 B의 부모노드 ⇒ A의 키(key)값과 B의 키값 사이에는 대소관계 성립

 

• 힙의 종류
  
  • 최대 힙 : 부모노드의 키 값 > 자식노드의 키 값
  • 최소 힙 : 부모노드의 키 값 < 자식노드의 키 값
  • 대소관계는 부모노드, 자식노드 간에만 성립 → 형제 사이에는 대소관계 정해지지 않음