목차
Multi-modal, 특히 vision-language model에 관심을 갖게 되면서 관련 논문을 찾아보던 중, task-agnostic, modality-agnostic한 다양한 input을 다룰 수 있는 모델인 Perceiver와, 이에 이어 output까지 원하는 형태로 만들 수 있는 Perceiver IO를 접하게 되었다.
Multi-modal 분야 뿐만 아니라 backbone으로(혹은 아이디어를 활용하여 구조를 변형하여) 훨씬 다양하게 활용될 수 있을 것 같아 두 아키텍쳐를 다룬 논문을 읽고 그 내용을 합쳐서 정리해보려 한다.
먼저, Transformer의 핵심인 self-attention과 cross-attention이 여기서도 핵심 개념이기 때문에, 이를 다룬 글을 읽어보는 것을 추천한다.
Transformers in Vision - (1) Attention & Transformer
Transformer가 computer vision에서 어떻게 쓰였는지, 관련 모델이 어떻게 발전하고 있는지 여러 포스팅에 걸쳐서 알아보고자 한다. 이번 포스팅에서는 가장 중요한 기초 내용인 attention과 transformer에 대
jjuke-brain.tistory.com
그리고, 더 자세한 내용은 2021년 ICML에 발표된 Perceiver 논문 "Perceiver: General Perception with Iterative Attention"과 2022년 ICLR에 발표된 Perceiver IO 논문 "Perceiver IO: A General Architecture for Structured Inputs & Outputs"를 참조하자.
Introduction
2D 비전에서의 spatial locality와 같은 inductive bias는 학습의 효율성을 극대화한다. 그러나 large dataset으로 학습을 진행하는 경우 이러한 inductive bias를 활용한 accuracy 뿐만 아니라 flexibility도 중요하다. (inductive bias가 강한 CNN이나 RNN같은 경우, large dataset에 대해 학습시키면 오히려 성능이 제한된다. 자세한 내용은 링크를 참조하자.)
이전까지는 input의 modality가 바뀌면 그것을 학습하기 위한 architecture도 바뀌었다. 예를 들어, ResNet과 ViT는 2D grid 구조의 image에, LSTM은 text 등의 sequential data에 특화되어있다.
하지만 Perceiver는 Input data의 modality, dataset 및 크기(dimension, size, number)에 상관 없이 활용 가능한 transformer 기반의 모델이다.
본격적으로 알아보기에 앞서, 간단하게 Perceiver의 특징을 살펴보자.
Transformer는 공간적, 시간적 복잡도가 \(O(n^2)\)이다. ViT에서는 patch로 나누는 등의 방법으로 이를 해결했지만, Perceiver는 고차원 input의 expressivity와 flexibility를 유지하면서 인지하는 방법을 제안한다.
Perceiver의 주요 아이디어는 latent space에서 input이 통과하는 attention bottleneck을 생성하는 것이다. 기존 transformer와 달리 all-to-all attention이 필요 없으므로 quadratic scaling 문제를 해결한다. 또한 network depth와 input size가 분리되어 있으므로 input size에 상관 없이 deep하게 설계할 수 있다.
Asymmetric attention mechanism을 사용하여 Input(Byte array)을 latent bottleneck으로 distillation하는 과정을 반복한다. 이때, 매우 큰 입력도 받을 수 있다는 특징이 있다.
Fourier feature를 통해 position encoding을 해준다. 모든 입력 데이터와 position, modality feature를 연관시킴으로써 입력 데이터의 구조(spatial or temporal information)를 반영한다.
Method
Overview
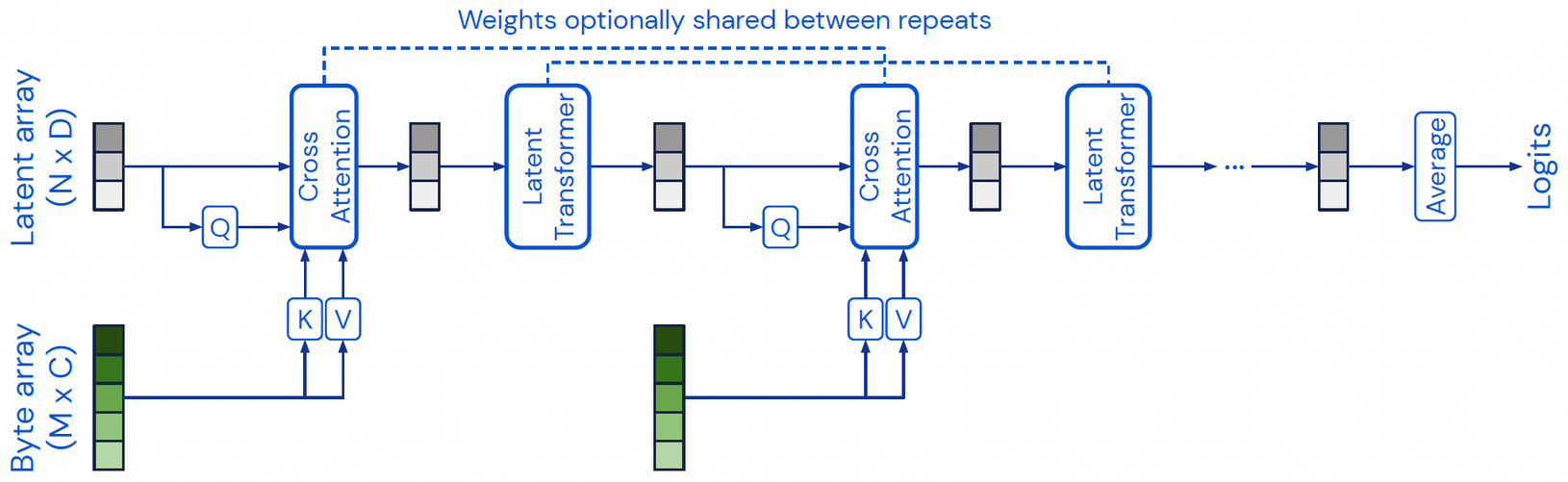
우선, 활용하는 변수들을 정리해보자.
- Byte(Input) array \(\mathbf{x} \in \mathbb{R}^{M \times C}\) : 임의의 size를 가진다.
- \(M\) : Input array의 index dimensionality
- \(C\) : Input array의 channel dimensionality
- \(M\)과 \(C\)는 input data의 종류(dataset, modality 등)에 따라 달라진다. 예를 들어, ImageNet을 활용하는 경우 224 by 224 RGB image를 사용하므로 \(M\)은 50,176, \(C\)는 3이다.
- Latent array \(\mathbf{z} \in \mathbb{R}^{N \times D}\) : Latent space 내에서 update되는 array이다.
- \(N\) : Latent array의 index dimensionality
- \(D\) : Latent array의 channel dimensionality
- \(N\)과 \(D\)는 hyperparameter이다. 논문에서 \(N\)은 512, 1024 등이 쓰였고, \(D\)는 8, 16, 32, 64 등이 쓰였다.
- Latent array는 학습된 position encoding으로 초기화(initialize)된다.
- \(N \ll M\) : 당연한 얘기이지만, latent의 dimension이 input보다 훨씬 작다. 이를 통해 기존 Transformer보다 작은 복잡도를 가질 수 있다.
Perceiver의 주요 구성 요소는 다음과 같다.
- Cross attention module : Latent array와 byte(input) array를 latent array로 맵핑한다. 이는 Non-causal이며 mask를 사용하지 않는다.
- Self-attention module (Latent Transformer) : Latent array를 latent array로 맵핑한다.
- Iterative cross-attention & Weight sharing : "Cross-attention module → Self-attention modules" block을 반복하며, 효율을 위해 각 block의 cross-attention module끼리, self-attention module들끼리 weight를 공유한다.
- Position encoding : 기존 Transformer와 같은 방법(Fourier feature position encoding)으로 위치 구조(language domain을 예로 들면 '어순')를 부여해준다.
핵심 연산인 attention을 구현한 코드를 살펴보자. Huggingface에서 제공하는 Perceiver IO 코드에서는 self-attention과 cross-attention을 다음 클래스로 구현하였다.
class PerceiverSelfAttention(nn.Module):
"""Multi-headed {cross, self}-attention. Can be used both in the encoder as well as in the decoder."""
def __init__(
self,
config,
is_cross_attention=False,
qk_channels=None,
v_channels=None,
num_heads=1,
q_dim=None,
kv_dim=None,
):
super().__init__()
self.num_heads = num_heads
# Q and K must have the same number of channels.
# Default to preserving Q's input's shape.
if qk_channels is None:
qk_channels = q_dim
# V's num_channels determines the shape of the output of QKV-attention.
# Default to the same number of channels used in the key-query operation.
if v_channels is None:
v_channels = qk_channels
if qk_channels % num_heads != 0:
raise ValueError(f"qk_channels ({qk_channels}) must be divisible by num_heads ({num_heads}).")
if v_channels % num_heads != 0:
raise ValueError(f"v_channels ({v_channels}) must be divisible by num_heads ({num_heads}).")
self.qk_channels = qk_channels
self.v_channels = v_channels
self.qk_channels_per_head = self.qk_channels // num_heads
self.v_channels_per_head = self.v_channels // num_heads
# Layer normalization
self.layernorm1 = nn.LayerNorm(q_dim)
self.layernorm2 = nn.LayerNorm(kv_dim) if is_cross_attention else nn.Identity()
# Projection matrices
self.query = nn.Linear(q_dim, qk_channels)
self.key = nn.Linear(kv_dim, qk_channels)
self.value = nn.Linear(kv_dim, v_channels)
self.dropout = nn.Dropout(config.attention_probs_dropout_prob)
def transpose_for_scores(self, x, channels_per_head):
new_x_shape = x.size()[:-1] + (self.num_heads, channels_per_head)
x = x.view(*new_x_shape)
return x.permute(0, 2, 1, 3)
def forward(
self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.FloatTensor] = None,
head_mask: Optional[torch.FloatTensor] = None,
inputs: Optional[torch.FloatTensor] = None,
inputs_mask: Optional[torch.FloatTensor] = None,
output_attentions: Optional[bool] = False,
) -> Tuple[torch.Tensor]:
hidden_states = self.layernorm1(hidden_states)
inputs = self.layernorm2(inputs)
# Project queries, keys and values to a common feature dimension. If this is instantiated as a cross-attention module,
# the keys and values come from the inputs; the attention mask needs to be such that the inputs's non-relevant tokens are not attended to.
is_cross_attention = inputs is not None
queries = self.query(hidden_states)
if is_cross_attention:
keys = self.key(inputs)
values = self.value(inputs)
attention_mask = inputs_mask
else:
keys = self.key(hidden_states)
values = self.value(hidden_states)
# Reshape channels for multi-head attention.
# We reshape from (batch_size, time, channels) to (batch_size, num_heads, time, channels per head)
queries = self.transpose_for_scores(queries, self.qk_channels_per_head)
keys = self.transpose_for_scores(keys, self.qk_channels_per_head)
values = self.transpose_for_scores(values, self.v_channels_per_head)
# Take the dot product between the queries and keys to get the raw attention scores.
attention_scores = torch.matmul(queries, keys.transpose(-1, -2))
batch_size, num_heads, seq_len, q_head_dim = queries.shape
_, _, _, v_head_dim = values.shape
hiddens = self.num_heads * v_head_dim
attention_scores = attention_scores / math.sqrt(q_head_dim)
if attention_mask is not None:
# Apply the attention mask (precomputed for all layers in PerceiverModel forward() function)
attention_scores = attention_scores + attention_mask
# Normalize the attention scores to probabilities.
attention_probs = nn.Softmax(dim=-1)(attention_scores)
# This is actually dropping out entire tokens to attend to, which might
# seem a bit unusual, but is taken from the original Transformer paper.
attention_probs = self.dropout(attention_probs)
# Mask heads if we want to
if head_mask is not None:
attention_probs = attention_probs * head_mask
context_layer = torch.matmul(attention_probs, values)
context_layer = context_layer.permute(0, 2, 1, 3).contiguous()
new_context_layer_shape = context_layer.size()[:-2] + (hiddens,)
context_layer = context_layer.view(*new_context_layer_shape)
outputs = (context_layer, attention_probs) if output_attentions else (context_layer,)
return outputs
먼저, init 함수에서는 query&key channel(둘은 같아야 dot product 연산을 할 수 있다!), value channel, Layer normalization, MLP(query, key, value network), dropout 등을 선언해준다.
forward에서는 latent array와 input array에 layer normalization을 적용해주고, cross-attention인지 self-attention인지에 따라 qkv attention 연산을 진행한다.
Cross Attention Module (Encoding or Read in Perceiver IO)
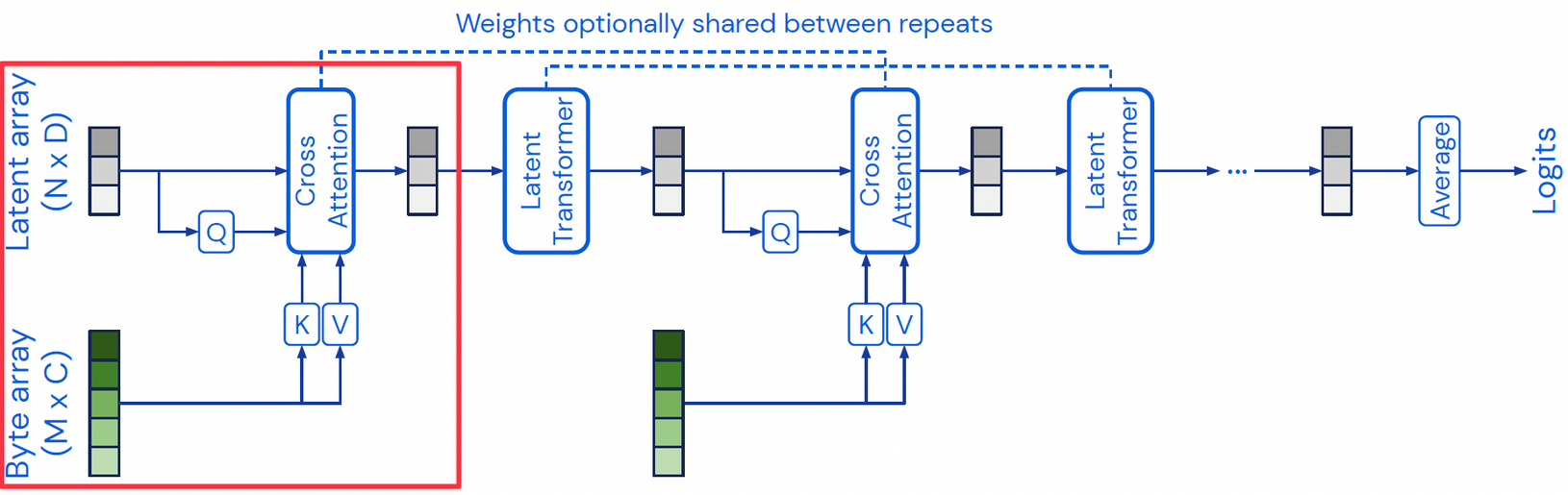

주요 구성 요소 중 cross-attention module부터 살펴보자. 여기서 Cross-attention은 latent array \(\mathbf{z}\)가 query network(MLP)를 거쳐(projection) query \(\mathbf{q} \in \mathbb{R}^{N \times d_\text{qk}}\), input array \(\mathbf{x}\)가 key, value network(MLP)를 거쳐 각각 key \(\mathbf{k} \in \mathbb{R}^{M \times d_\text{qk}} \), value \(\mathbf{v} \in \mathbb{R}^{M \times d_\text{v}}\)가 되고, 이러한 query, key, value에 대해 \( \mathbf{q} \neq \mathbf{k} = \mathbf{v} \)인 경우의 attention 메커니즘이다.
Attention score는 다음과 같이 계산한다. (자세한 내용은 링크를 참조하자.)
\( \operatorname{softmax}(\mathbf{q} \mathbf{k}^\top) \mathbf{v} \)
기존 Transformer의 QKV attention (Query, Key, Value attention) 계산 복잡도는 \(\mathcal{O}(M^2)\), 즉 input size \(M\)에 2차로 비례(quadratically increase)하는데, Perceiver는 latent array와 cross-attention을 해주므로 계산 복잡도가 \(\mathcal{O}(MN)\), 즉 input size \(M\)에 linear하다.
Encoder의 코드를 요약하면 다음과 같다.
class PerceiverEncoder(nn.Module):
"""The Perceiver Encoder: a scalable, fully attentional encoder."""
def __init__(self, config, kv_dim=None):
super().__init__()
self.config = config
# Construct the cross attention layer.
self.cross_attention = PerceiverLayer(
config,
is_cross_attention=True,
...
)
# Construct a single block of self-attention layers.
# We get deeper architectures by applying this block more than once.
self_attention_layers = []
for _ in range(config.num_self_attends_per_block):
layer = PerceiverLayer(
config,
is_cross_attention=False,
...
)
self_attention_layers.append(layer)
self.self_attends = nn.ModuleList(self_attention_layers)
def forward(
self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.FloatTensor] = None,
head_mask: Optional[torch.FloatTensor] = None,
inputs: Optional[torch.FloatTensor] = None,
inputs_mask: Optional[torch.FloatTensor] = None,
output_attentions: Optional[bool] = False,
output_hidden_states: Optional[bool] = False,
return_dict: Optional[bool] = True,
) -> Union[Tuple, BaseModelOutputWithCrossAttentions]:
all_hidden_states = () if output_hidden_states else None
all_self_attentions = () if output_attentions else None
all_cross_attentions = () if output_attentions else None
# Apply the cross-attention between the latents (hidden_states) and inputs:
layer_outputs = self.cross_attention(
...
)
hidden_states = layer_outputs[0]
# Apply the block of self-attention layers more than once:
for _ in range(self.config.num_blocks):
for i, layer_module in enumerate(self.self_attends):
layer_head_mask = head_mask[i] if head_mask is not None else None
layer_outputs = layer_module(
...
)
hidden_states = layer_outputs[0]
return BaseModelOutputWithCrossAttentions(
last_hidden_state=hidden_states,
hidden_states=all_hidden_states,
attentions=all_self_attentions,
cross_attentions=all_cross_attentions,
)
Self-attention Module (Process in Perceiver IO)

Latent Transformer는 Cross attention module의 결과인 bottleneck(latent space)에 사용되는 deep transformer (latent self-attention blocks)이다.

Fig 4에서 볼 수 있듯이, Depth(self-attention의 layer 개수 \(L\))와 input size \(M\)을 완전히 분리시킴으로써 input size에 상관 없이 깊은 layer를 쌓을 수 있게 되었다. Self-attention은 query \(\mathbf{q} \in \mathbb{R}^{N \times D}\), key \(\mathbf{k} \in \mathbb{R}^{N \times D}\), value \(\mathbf{v} \in \mathbb{R}^{N \times D}\)가 모두 같은 (\(\mathbf{q} = \mathbf{k} = \mathbf{v}\) 경우이다.
계산 과정은 cross-attention과 동일하다.
\( \operatorname{softmax}(\mathbf{q} \mathbf{k}^\top) \mathbf{v} \)
그리고 Latent Transformer는 GPT-2 architecture(Transformer의 decoder 부분을 기반으로 한 architecture)를 사용하였다.
Self-attention의 복잡도는 layer 개수 \(L\)을 고려하면 \(\mathcal{O}(LN^2)\)로 볼 수 있다. 따라서 cross-attention module 및 self-attention module을 모두 고려한 Perceiver의 최종 복잡도는 \(\mathcal{O}(MN + LN^2)\)로, input size \(M\)에 linear하게 복잡도가 증가한다.
Iterative Cross-attention & Weight Sharing

Iterative cross-attention이란, Latent array로 정보를 압축하다보니 한 번의 "cross-attention module, self-attention module" block(cross-attention layer)은 input signal의 detail을 놓칠 수 있다. 이를 해결하기 위해 Fig 6처럼 detail 정보도 학습하기 위해 cross-attention layer를 여러 개 사용한다.
Weight sharing이란, parameter efficiency를 위해 서로 다른 cross-attention layer(self-attention module과 cross-attention module)끼리 weight를 공유하는 것을 말한다.
Cross attention 개수에 따라, cross-attention layer를 어떻게 구성하는가에 따라 performance를 비교해보자.
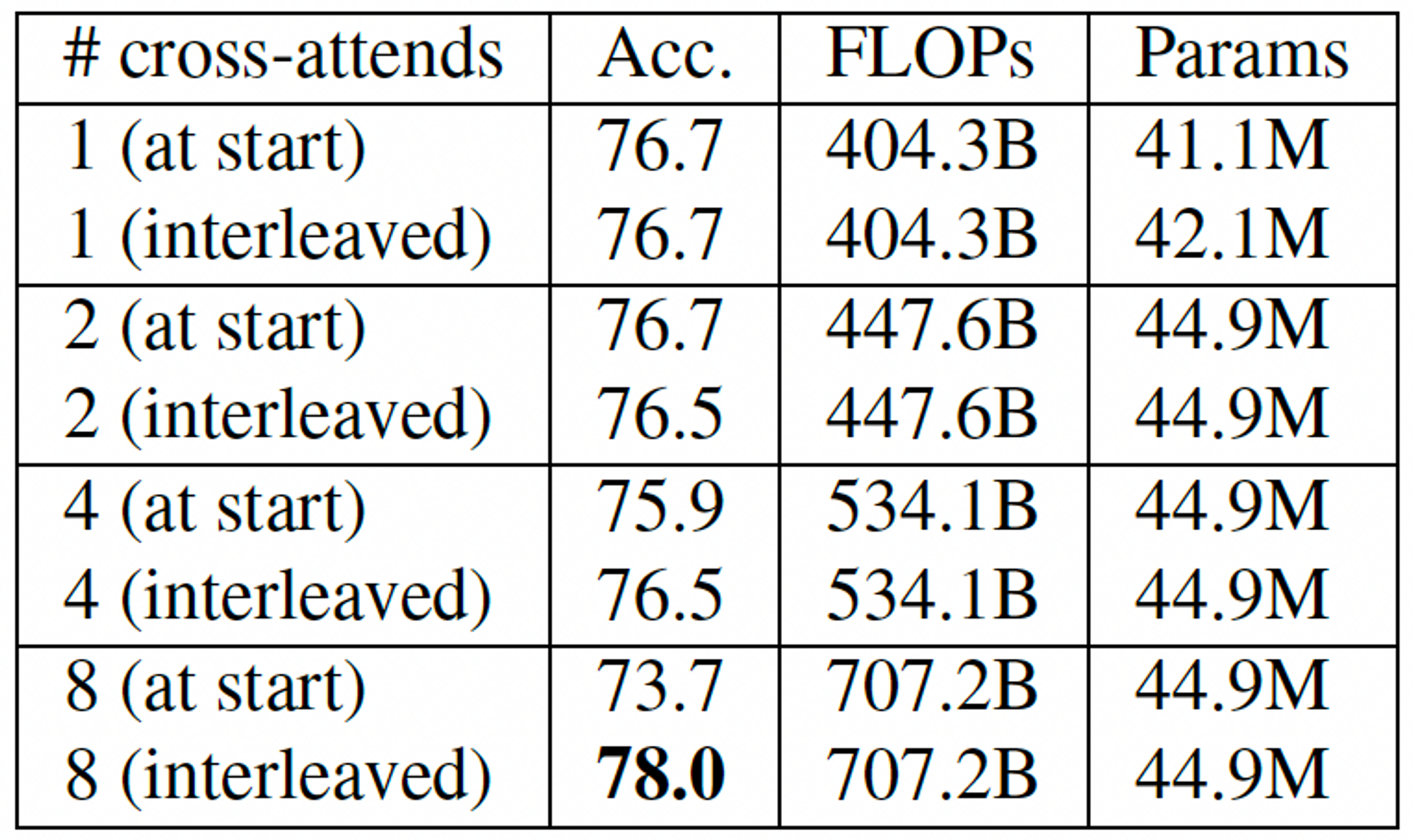
- Interleaved는 Fig 6처럼 cross-attention → self-attention layers → cross-attention → self-attention layers → ... 순으로 pipeline이 진행되는 것이고, at start는 시작 부분에 모든 cross-attention layer들을 적용한 후에 self-attention layers를 적용하는 것이다.
- 첫 layer 제외한 모든 cross-attention layer의 weight은 공유된다. 처음 layer까지 공유하면 성능이 확 떨어진다고 한다. (개인적으로 이유를 분석해보자면, '처음 latent array는 input에 대한 정보가 전혀 없는 상태이므로, 첫 cross-attention layer에서는 전반적인 input의 정보를 받아들이려 할 것이고, 그 이후에는 점점 detail한 정보를 얻으려 할 것이므로'라고 생각해볼 수 있다.)
- Cross attention 개수가 많아질수록 성능이 좋아지지만 당연히 computational cost도 증가한다.
Position Encodings
Permutation invariance and position information
Attention은 기본적으로 permutation-invariant operation이다. 이는 input의 순서가 바뀌어도 같은 output을 반환한다. 이러한 특성 덕분에 다양한 종류의 data에 적용할 수 있으나, 특정 domain에 최적화되어있지는 않다.
Fourier feature position encodings는 Fourier transform 기반으로 input data의 위치 정보를 부여한다. 이는 기존 Transformmer에서 활용한 방식과 같고, 자세한 내용은 다음 글을 참조하자.
https://kazemnejad.com/blog/transformer_architecture_positional_encoding/
Transformer Architecture: The Positional Encoding - Amirhossein Kazemnejad's Blog
Transformer architecture was introduced as a novel pure attention-only sequence-to-sequence architecture by Vaswani et al. Its ability for parallelizable training and its general performance improvement made it a popular option among NLP (and recently CV)
kazemnejad.com
Perceiver에서 fourier feature position encoding은 다음과 같이 구현되어 있다.
class PerceiverFourierPositionEncoding(PerceiverAbstractPositionEncoding):
"""Fourier (Sinusoidal) position encoding."""
def __init__(self, num_bands, max_resolution, concat_pos=True, sine_only=False):
super().__init__()
self.num_bands = num_bands
self.max_resolution = max_resolution
self.concat_pos = concat_pos
self.sine_only = sine_only
@property
def num_dimensions(self) -> int:
return len(self.max_resolution)
def output_size(self):
"""Returns size of positional encodings last dimension."""
num_dims = len(self.max_resolution)
encoding_size = self.num_bands * num_dims
if not self.sine_only:
encoding_size *= 2
if self.concat_pos:
encoding_size += self.num_dimensions
return encoding_size
def forward(
self,
index_dims: List[int],
batch_size: int,
device: torch.device,
dtype: torch.dtype,
pos: torch.FloatTensor = None,
) -> torch.FloatTensor:
pos = _check_or_build_spatial_positions(pos, index_dims, batch_size)
fourier_pos_enc = generate_fourier_features(
pos,
num_bands=self.num_bands,
max_resolution=self.max_resolution,
concat_pos=self.concat_pos,
sine_only=self.sine_only,
).to(device=device, dtype=dtype)
return fourier_pos_enc
def _check_or_build_spatial_positions(pos, index_dims, batch_size):
"""
Checks or builds spatial position features (x, y, ...).
Args:
pos (`torch.FloatTensor`):
None, or an array of position features. If None, position features are built. Otherwise, their size is checked.
index_dims (`List[int]`):
An iterable giving the spatial/index size of the data to be featurized.
batch_size (`int`):
The batch size of the data to be featurized.
Returns:
`torch.FloatTensor` of shape `(batch_size, prod(index_dims))` an array of position features.
"""
if pos is None:
pos = build_linear_positions(index_dims)
# equivalent to `torch.broadcast_to(pos[None], (batch_size,) + pos.shape)`
# but `torch.broadcast_to` cannot be converted to ONNX
pos = pos[None].expand((batch_size,) + pos.shape)
pos = torch.reshape(pos, [batch_size, np.prod(index_dims), -1])
else:
# Just a warning label: you probably don't want your spatial features to
# have a different spatial layout than your pos coordinate system.
# But feel free to override if you think it'll work!
if pos.shape[-1] != len(index_dims):
raise ValueError("Spatial features have the wrong number of dimensions.")
return pos
def build_linear_positions(index_dims, output_range=(-1.0, 1.0)):
"""
Generate an array of position indices for an N-D input array.
Args:
index_dims (`List[int]`):
The shape of the index dimensions of the input array.
output_range (`Tuple[float]`, *optional*, defaults to `(-1.0, 1.0)`):
The min and max values taken by each input index dimension.
Returns:
`torch.FloatTensor` of shape `(index_dims[0], index_dims[1], .., index_dims[-1], N)`.
"""
def _linspace(n_xels_per_dim):
return torch.linspace(start=output_range[0], end=output_range[1], steps=n_xels_per_dim, dtype=torch.float32)
dim_ranges = [_linspace(n_xels_per_dim) for n_xels_per_dim in index_dims]
array_index_grid = meshgrid(*dim_ranges, indexing="ij")
return torch.stack(array_index_grid, dim=-1)

여기까지가 Perceiver의 내용이다. 간단히 요약하자면, Perceiver는 latent space 내에서 cross-attention 및 self-attention을 적용함으로써 어떤 크기, dataset, modality의 input이던 상관 없이 다룰 수 있게 되었다. 하지만, 마지막 output은 single category(label)으로, classification task에만 활용이 가능하다는 한계가 있다. 이를 해결하여 output도 원하는 structure(shape)로 출력할 수 있게 보완한 모델이 바로 Perceiver IO이다.
Perceiver IO에서는 Perceiver의 cross-attention module(encoding), self-attention module을 그대로 사용하며, 마지막에 또 다른 cross-attention module(decoding) 과정을 추가한다. 저자는 이를 read-process-write architecture라 한다.
- Read ( \( \mathbf{x} \in \mathbb{R}^{M \times C} \rightarrow \mathbf{z} \in \mathbb{R}^{N \times D} \) ) : Input을 latent space로 인코딩하는 과정 (Perceiver의 cross-attention module과 같다.)
- Process ( \( \mathbf{z} \rightarrow \mathbf{z}' \) ) : Latent representation을 정제(refine)하는 과정 (Perceiver의 Latent Transformer와 같다.)
- Write ( \( \mathbf{z} \in \mathbb{R}^{N \times D} \rightarrow \mathbf{y} \in \mathbb{R}^{O \times E} \) ) : Latent space를 디코딩하는 과정
- Read에서처럼 계산 과정과 output size를 분리하여 매우 큰 size도 출력이 가능하다!
다음 글에서는 Perceiver IO의 Write 부분부터 살펴보자.






최근댓글