'Ch07. Monte Carlo Methods (1)'에 이어 내용을 정리해보자.
https://jjuke-brain.tistory.com/78?category=957313
Ch07. Monte Carlo Methods (1)
이전까지 살펴본 Markov Decision Process와 Dynamic Programming에 이어, Monte Carlo Method를 살펴보자. 앞의 내용이 궁금하다면, 다음 링크를 참조하자. https://jjuke-brain.tistory.com/68?category=957313..
jjuke-brain.tistory.com
목차
3. Monte Carlo Control
이전에 Monte Carlo Method가 어떤 건지, 강화 학습에서 Monte Carlo를 이용하여 Prediction을 어떻게 할지 알아보았다.
Prediction(Evaluation)을 통해 value function을 추정할 수 있지만, 강화 학습은 궁극적으로 Optimal Policy를 찾아야 한다.
따라서 이번에는 optimal policy \(\pi\)를 찾는 방법에 대해 알아볼 것이다.
Monte Carlo estimation을 통해 optimal policy를 찾는 과정은 DP(Dynamic Programming)에서와 비슷하다.
아래 그림과 같이 policy evaluation과 policy improvement가 서로 상호작용하는 과정, 즉 GPI(Generalized Policy Iteration)를 반복해주면 된다.
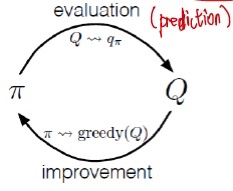
이를 풀어 쓰면 다음과 같다.
$$ \pi_0 \overset{E}{\rightarrow} q_{\pi_0} \overset{I}{\rightarrow} \pi_1 \overset{E}{\rightarrow} q_{\pi_1} \overset{I}{\rightarrow} \pi_2 \overset{E}{\rightarrow} \cdots \overset{I}{\rightarrow} \pi_* \overset{E}{\rightarrow} q_* $$
여기서 E는 policy evaluation을 나타내고, I는 policy improvement를 나타낸다.
policy는 value function에 대해 improve되고, value function은 policy를 따라 improve된다는 것을 알 수 있다.
1) Monte Carlo Exploration Starts
DP 방법과는 달리 model dynamics를 모르므로 state value를 구할 수 없고, action value, 즉 Q function에 집중한다.
state value는 우리가 선택하는 policy에 따라 달라지므로, state value를 추정하는 것보다 Action value function, 즉 Q funciton을 추정하는 것이 더 직관적이다.
예를 들어, blackjack 카드 게임(내가 가진 카드의 숫자 합이 딜러보다 21에 가까우면 이기는 카드 게임)에서, 카드 숫자 합이 20이라고 가정해보자. 이 state의 value는 얼마인가?
- 이러한 state value는 policy에 따라 달라진다. 무조건 hit하는 policy를 갖고 있다면, 좋은 state가 아니므로 값이 매우 낮을 것이다. 하지만 stand하는 policy를 선택한다면 21에 매우 가까우므로 아주 좋은 state이고, 값이 높을 것이다.
- 따라서, state value는 policy에 의존적임을 알 수 있다.
Value function과 Action value function(Q function) 수식을 다시 한 번 살펴보자.
$$ V^\pi (s) = \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum} P^a_{ss'}[R^a_{ss'} + \gamma \underset{a'}{\sum} Q^\pi(s', a')] $$
$$ Q^\pi(s, a) = \underset{s'}{\sum} P^a_{ss'}[R^a_{ss'} + \gamma \underset{a'}{\sum} \pi(s', a') Q^\pi(s', a')] $$
수식에서도 action value function은 policy에 의존하지 않는다는 것을 알 수 있다. (\(\gamma\)가 붙은 부분은 미래의 값에 대한 term 이다.)
하지만, problem of exploration이 발생한다.
exploration 문제란, state-action value를 구하려면 state에 방문을 해보아야 하는데, 모든 state에서 모든 가능한 action을 explore해보지 않는 한, 더 좋은 policy를 놓칠 수 있다는 문제이다.
즉, best action을 알기 위해서는 각 state에서 가능한 모든 action을 explore해보아야 하는데, 하나의 에피소드 내에서는 불가능한 일이다.
이때 사용하는 방법이 바로 Monte Carlo Exploring Starts (MC-ES)이다.
MC-ES는 각 에피소드를 시작할 때, initial state를 랜덤으로 정한다. 충분히 많은 에피소드를 진행하면 모든 state에서 가능한 action을 해볼 수 있을 것이다.
과정을 좀 더 자세히 살펴보자.
- Q fuction과 policy를 랜덤 값으로 초기화하고, 빈 리스트에 return을 초기화한다.
- 랜덤으로 초기화된 policy에 따라 에피소드를 진행한다.
- 에피소드 내에서 모든 유일한 state-action pair(즉, first-visit MC)에 대해 return을 계산하고 리스트에 넣는다.
- 동일한 state-action pair은 redundant information을 가지므로 제외시킨다.
- return 리스트에 있는 return들의 평균값을 구하고 Q function의 값으로 할당한다.
- greedy policy, 즉 해당 Q(s, a) pair 중에서 가장 높은 값을 갖는 policy를 골라 improved policy를 찾는다.
- 이러한 과정을 충분히 많은 에피소드로 반복하여 모든 state-action pair를 커버할 수 있도록 한다.
여기서 2~4는 Policy Evaluation (Prediction), 5는 Policy Improvement 과정이다.
이를 Pseudo Code로 나타내면 다음과 같다.
Initialize:
π(s) ∈ A(s) (arbitrarily), for all s ∈ S
Q(s, a) ∈ R (arbitrarily), for all s ∈ S, a ∈ A(s) # R: real number
Returns(s, a) ← empty list, for all s ∈ S, a ∈ A(s)
Loop forever(for each episode):
# 첫 (state, action) pair random하게 선택: MC-ES
Choose S_0 ∈ S, A_0 ∈ A(S_0) randomly such that all pairs have probability > 0
Generate an episode from (S_0, A_0), following π: S_0, A_0, R_1, ...,S_{T-1}, A{T-1}, R_T
G ← 0
Loop for each step of episode, t = T-1, T-2, ..., 0:
G ← γG + R_{t+1} # cumulative return
Unless the pair S_t, A_t appears in S_0, A_0, ... , S_{t-1}, A_{t-1}: # first-visit
Append G to Returns(S_t, A_t)
Q(S_t, A_t) ← average(Returns(S_t, A_t))
π(S_t) ← argmax_a Q(S_t, a) # policy improvement (greedy)
2) On-policy Monte Carlo Control
Monte Carlo exploration starts는 state-action pair가 매우 많은 경우, 모든 combination을 explore하기에 계산 비용이 너무 커진다는 한계점이 있다. 일상적인 task를 생각해보면 state-action pair가 매우 큰 경우가 많으므로, 이러한 비현실적인 한계점을 극복할 필요가 있다.
이러한 한계점을 극복한 방법이 두 가지 있는데, 이를 on-policy Monte Carlo Control, off-policy Monte Carlo Control이라 한다.
먼저 on-policy Monte Carlo contorl 방법은 policy improvement 과정에서 단순히 greedy policy를 사용하는 대신, ε-greedy policy를 사용하는 것이다.
이로써 MC-ES는 처음 state-action pair를 랜덤으로 초기화하는 것만 진행했다면, on-policy MC에서는 매 state, 매 action에 대해 exploration 가능성을 만들어준다.
(1) Greedy Policy
기존 MC-ES에서 사용했던 greedy policy를 살펴보면,
\(\pi\)를 update할 때 무조건 가장 큰 값을 취한다.
$$ \pi(S_t) \leftarrow \underset{a}{argmax} Q(S_t, a) $$
| State | Action | Value |
| State 1 | Action 0 | 0.5 |
| State 1 | Action 1 | 0.1 |
| State 1 | Action 2 | 0.8 |
즉, 위와 같이 state 1에 대한 Q table이 주어져 있다면, State 1에서는 무조건 Action 2만 취하게 된다.
하지만 아직 explore 해보지 않은 action 중 실제로 더 좋은 action이 존재할 수도 있다.
따라서, 적절한 (작은) \(\epsilon\) 값을 정하여 exploration과 exploitation을 적절히 하도록 설정해주어야 한다.
(exploration-exploitation dilemma, 이 둘은 서로 trade-off 관계)
exploration은 새로운 state-action pair를 경험하는 것이고, exploitation은 현재 좋은 값에 집중하는 것이다.
(2) \(\epsilon\)-greedy policy
이러한 exploration-exploitation dilemma를 극복하기 위해 \(\epsilon\)-greedy policy가 사용된다.
매우 작은 값인 \(\epsilon\) 만큼의 확률로 exploration을 하며 새로운 action을 랜덤하게 진행하고, 대부분 (\(1 - \epsilon\))은 exploitation, 즉 greedy policy를 따라 Q값을 최대로 하는 action을 선택하도록 하는 것이다.
앞서 들었던 예시에 이어서, \(epsilon\)의 확률로 새로운 action 4를 했을 때, 더 좋은 값이 다음과 같이 발견될 수도 있다.
| State | Action | Value |
| State 1 | Action 0 | 0.5 |
| State 1 | Action 1 | 0.1 |
| State 1 | Action 2 | 0.8 |
| State 1 | Action 4 | 0.93 |
On-policy Monte Carlo Control의 Pseudo Code는 다음과 같다.
Algorithm parameter: small ε > 0 # hyperparameter
Initialize:
π ← an arbitrary ε-soft policy # (=ε-greedy policy)
Q(s, a) ∈ R (arbitrarily), for all s ∈ S, a ∈ A(s) # R: real number
Returns(s, a) ← empty list, for all s ∈ S, a ∈ A(s)
Loop forever(for each episode):
# 굳이 랜덤 초기화 하지 않음
Generate an episode following π: S_0, A_0, R_1, ...,S_{T-1}, A{T-1}, R_T
G ← 0
Loop for each step of episode, t = T-1, T-2, ..., 0:
G ← γG + R_{t+1} # cumulative return
Unless the pair (S_t, A_t) appears in S_0, A_0, ... , S_{t-1}, A_{t-1}: # first-visit
Append G to Returns(S_t, A_t)
Q(S_t, A_t) ← average(Returns(S_t, A_t))
# policy improvement
A* ← argmax_a Q(S_t, a) (with ties broken arbitrarily) # A*의 의미: max값 여러개라면 random하게 하나의 action 선택
For all a ∈ A(S_t): # S_t에서 가능한 모든 action A 중
# 대부분은 (1-ε)의 확률로 A*(greedy)인 action으로 π를 update
π(a|S_t) ← 1 - ε + ε/|A(S_t)| if a = A*
# 일부는 ε의 확률로 A*(greedy)가 아닌 것으로 π를 update함
π(a|S_t) ← ε/|A(S_t)|
\(\pi\)의 정의는 state \(S_t\)에서 action \(a\)가 선택될 확률이다.
\(|A(S_t)|\)는 \(S_t\)에서 가능한 action의 개수를 말한다.
\(S_t\)에서 선택 가능한 action 각각의 확률을 모두 더하면 1이 되어야 하므로, 아래 수식이 성립한다.
$$ {\epsilon \over N} * (N-1) + (1 - \epsilon + {\epsilon \over N}) = 1 $$
(N개 중 greedy action 1개, 나머지 action N-1개 존재)
3) Off-policy Monte Carlo Control
Off-policy는 좀 더 복잡하고 새로운 개념으로, 더 복잡한 문제에 대해 잘 작동하여 Deep Reinforcement Learning 분야에서 많이 사용된다.
Off-policy는 서로 독립적인 policy 두 개를 갖는다.
- Target Policy (\(\pi\)): improvement의 대상이자 Optimal Policy가 될 policy (Agent가 학습할 policy)
- Behavior Policy (\(b\)): agent의 행동을 생성하는, 더 탐험적인(exploratory) policy
On-policy에서는 하나의 policy \(\pi\)로 행동과 update(improvement)를 반복하였다. 즉, target policy와 behavior policy가 같은 상태인 것이다.
하지만 Off-policy는 update(improvement)의 대상인 target policy가 있고, 에피소드를 생성하는 behavior policy는 따로 있으며, 이 둘은 독립적이다.
여기서 behavior policy는 모든 가능한 state-action pair를 explore하는 역할을 맡으며, 이에 따라 \(epsilon\)-greed policy, 즉 soft policy로 불린다.
target policy는 greedy policy로 불린다.
update하고싶은 target policy를 최적화하는 데 사용하는 data(생성된 에피소드)가 target policy와 상관이 없다(Off)는 의미에서 off-policy라는 이름이 붙었다.
목표는 target policy \(\pi\)에 대해 Q function을 추정하는 것인데, agent는 완전히 다른 behavior policy \(b\)를 따른다.
통계적 개념인 'Importance Sampling'에 따라 \(n\)에서 나온 episode 중 \(\pi\)와 겹치는 에피소드(common episodes)를 통해 \(\pi\)를 추정할 수 있다.
이를 위해서는 다음과 같은 'assumption of coverage'라는 가정이 필요하다.
\(\pi(a|s) > 0\) 이면 \(b(a|s) > 0\)이다. 즉 target policy에 따라 s에서 a가 가능하면 behavior policy에서도 항상 s에서 a가 가능해야 한다. (값이 같을 필요는 없다.)
\(b\)는 stochastic(more exploratory) policy (예를 들어 \(\epsilon -greedy \, policy\), \(\pi\)는 deterministic greedy policy이다.
(1) Importance Sampling
Importance Sampling이란, 어떤 분포에서 다른 분포의 표본으로 값을 추정하는 technique이다.
이를 Off-policy MC 중 prediction 과정의 관점에서 본다면, \(\pi\)를 prediction하는 데 \(b\)에서 나온 에피소드를 사용하는 개념이다.
Importance Sampling은 Ordinary importance sampling, weighted importance sampling으로 나뉜다.
먼저, control은 제외하고 prediction 과정, 즉 고정 policy에 대한 value estimation에 대해 생각하자. prediction이 \(\pi\)와 \(b\)가 고정된, 간단한 경우이기 때문이다.
깊은 내용은 통계학에서의 importance sampling을 참조하도록 하고,
$$ (b에서 \, 계산한 return) * ( importance-sampling \, ratio) $$
를 통해 target policy 관련 value를 얻을 수 있다.
여기서 importance-sampling ratio는 \(b\)로 해당 trajectory가 나온 에피소드 개수와 \(\pi\)로 해당 trajectory가 나온 에피소드 개수의 비율로,
\(b\)로 나온 경우가 \(\pi\)에서 얼마나 공통적으로 나타나는지를 의미한다.
어떤 policy \(\pi\)에서, 주어진 starting state \(S_t\)에 대해 subsequent state-action trajectory인 '\(A_t, S_{t+1}, A_{t+1}, ..., S_T\)'의 확률 (한마디로 trajectory probability)은 다음과 같이 나타낼 수 있다.
$$ \begin{align*} Pr\{ A_t, & S_{t+1}, A_{t+1}, ..., S_T | S_t, A_{t:T-1} \sim \pi \} \\ &= \pi(A_t|S_t)p(S_{t+1}|S_t,A_t)\pi(A_{t+1}|S_{t+1}) \cdots p(S_T|S_{T-1}, A_{T-1}) \\ &= \underset{k=t}{\overset{T-1}{\prod}} \pi(A_k|S_k)p(S_{k+1}|S_k,A_k) \end{align*} $$
여기서 \(p\)는 state transition probability이다.
따라서, target policy와 behavior policy의 비율인 importance-sampling ratio는 다음과 같이 구할 수 있다.
$$ \rho_{t:T-1} = { \prod^{T-1}_{k=t} \pi(A_k|S_k)p(S_{k+1}|S_k,A_k) \over \prod^{T-1}_{k=t} b(A_k|S_k)p(S_{k+1}|S_k,A_k) } = \prod^{T-1}_{k=t} {\pi(A_k|S_k) \over b(A_k|S_k) } $$
여기서, \(p(S_{k+1}|S_k,A_k)\)부분은 transition probability를 모르므로 알 수 없는 값인데, target policy와 behavior policy의 경우 policy가 다를 뿐, environment(transition probability를 포함)는 같기 때문에 약분되어 계산이 가능해진다.
따라서, importance sampling ratio는 MDP가 아닌 두 policy와 sequence에 의해서만 결정된다.
이제 target policy에서의 expected return를 계산해야 할텐데, 계산을 통해 얻을 수 있는 \(G_t\)의 경우 behavior policy의 return이다.
따라서 \(\mathbb{E}[G_t|S_t=s]=v_b(s)\)이기 때문에 \(v_\pi\)와는 다른 값이다.
여기서도 importance-sampling ratio 값을 사용해준다.
behavior policy의 return을 계산하기 위한 위 식의 과정에 ratio를 곱해주면서 target policy의 return 값을 계산할 수 있다.
$$ \mathbb{E}[\rho_{t:T-1} G_t | S_t = s] = v_\pi(s) $$
이에 따라, ratio 값이 커진다는 의미는 \(b\)에서 일어난 것이 \(\pi\)에서도 많이 일어난다는 의미와 함께, G(return)값을 많이 반영한다는 의미도 갖고 있다.
간단히, \( \rho_{t:T-1} * v_b(s) = v_\pi(s) \)로 나타낼 수도 있다.
(2) Ordinary Importance Sampling and Weighted Importance Sampling
방문한 state \(s\)들의 집합을 \(\mathcal{J}(s)\)라 두자.
- every-visit method: \(s\)를 방문한 모든 time step을 저장
- first-visit method: 한 에피소드 내에서 \(s\)를 처음 방문한 time step을 저장
이때, 에피소드 경계에 따라 time step을 누적시키는 것이 편하다.
예를 들어, batch의 첫 번째 에피소드가 time 100에 끝나면, 다음 에피소드는 t = 101에서 시작하는 것으로 두는 것을 말한다.
또한, \(T(t)\)는 처음으로 termination이 일어나는 time step을 의미하고, \(G_t\)는 한 에피소드가 끝났을 때까지의 return을 의미한다.
\(v_\pi(s)\)를 계산하기 위해, ratio로 return을 스케일링하고 평균을 낼 것이다. 이것이 바로 Ordinary Importance Sampling이다.
$$ \mathbb{E}[\rho_{t:T-1} G_t | S_t = s] = v_\pi(s) $$
$$ V(s) = { \sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} G_t \over | \mathcal{J}(s) | } $$
또한 단순히 state 방문 횟수로 나누는 것이 아닌, ratio의 합으로 나눌 경우 Weighted Importance Samplling이라 한다.
$$ V(s) = { \sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} G_t \over \sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} } $$
이 둘의 차이점에 대해 알아보자.
실제 이런 일은 거의 없지만, \(t=1\), 즉 state \(s\)에 대해 single return이 주어진다고 가정하자.
weighted-average estimate에서는 분자와 분모가 약분되어 \(G_1\)만 남게 된다. 따라서 ratio의 의미가 사라진다.
이는 곧 \(b\)에 의한 return의 bias가 매우 큼을 의미한다.
이에 비해 ordinary importance-sampling은 항상 \(v_\pi(s)\)를 추정하지만, variance가 크다.
ratio 값이 10이라고 가정해보자. 이는 특정 trajectory가 target policy에서 발견되는 경우가 behavior policy에서보다 10배 많다는 것을 의미한다.
이 경우, 추정치 또한 10배가 되고, 에피소드의 trajectory가 target policy를 아주 잘 표현한다고 해도 너무 다른 값이 나온다.
결론적으로, 실제로는 single return인 경우가 거의 없으므로 추정치의 bias는 커도 상관이 없다. 따라서 weighted importance-sampling이 더 좋은 결과를 보이는 경우가 많다고 볼 수 있다.
Weighted Importance Sampling의 Pseudo Code를 살펴보자.
Input: an arbitrary target policy π # Prediction
Initialize, for all s ∈ S, a ∈ A(s):
Q(s, a) ∈ R (arbitrarily) # R: real number
C(s, a) ← 0
Loop forever(for each episode):
b ← any policy with coverage of π # behavior policy
Generate an episode following b: S_0, A_0, R_1, ...,S_{T-1}, A{T-1}, R_T # b에 따라 생성!
G ← 0
W ← 1
Loop for each step of episode, t = T-1, T-2, ..., 0, while W ≠ 0:
G ← γG + R_{t+1} # cumulative return
C(S_t, A_t) ← C(S_t, A_t) + W
Q(S_t, A_t) ← Q(S_t, A_t) + W/(C(S_t, A_t)) * [G - Q(S_t, A_t)] # weighted importance sampling
W ← W * (π(A_t|S_t) / b(A_t|S_t))
(3) Off-policy Monte Carlo Control
이제 Prediction에 이어 Control을 살펴보자.
Agent는 behavior policy를 따르면서 target policy를 improving하고, 학습한다.
이때 앞서 말한 coverage assumption을 충족해야 하고, 모든 가능성을 explore하기 위해 behavior policy가 soft해야 한다, 즉 모든 state에 대한 모든 action을 선택할 확률이 0보다 커야한다.
Target policy \(\pi \approx \pi^* \) 는 \(q_\pi\)의 추정치인 \(Q\)에 대해 greedy policy이다.
Behavior policy \(b\)는 어떤 것이든 될 수 있지만, \(\pi\)가 optimal policy로 수렴하도록 하기 위해 각 state-action pair로부터 무수히 많은 return을 얻어야 한다.
이는 \(b\)를 \(\epsilon-greedy \, policy\)로 설정하면 된다.
이에 따라 \(b\)는 stochastic policy, \(\pi\)는 deterministic policy임을 알 수 있다.
dynamic programmiong의 general policy iteration을 기반으로 off-policy MC Control을 수행하는 pseudo code는 다음과 같다. (weighted-importance sampling 사용)
Initialize, for all s ∈ S, a ∈ A(s):
Q(s, a) ∈ R (arbitrarily) # R: real number
C(s, a) ← 0
π(s) ← argmax_a Q(s, a) (with ties broken consistently) # greedy policy
Loop forever (for each episode):
b ← any soft policy # ε-greedy policy
Generate an episode using b: S_0, A_0, R_1, ... , S_{T-1}, A_{T-1}, R_T
G ← 0
W ← 1
Loop for each step of episode, t = T-1, T-2, ... , 0:
G ← γG + R_{t+1}
C(S_t, A_t) ← C(S_t, A_t) + W
Q(S_t, A_t) ← Q(S_t, A_t) + W/C(S_t, A_t) * [G - Q(S_t, A_t)] # Weighted Importance Sampling
π(S_t) ← argmax_a Q(S_t, a) (with ties broken consistently) # policy improvement
If A_t ≠ π(S_t) then exit inner Loop (proceed to next episode)
W ← W * 1/(b(A_t|S_t))







최근댓글