Ch07. Monte Carlo Methods (1)

이전까지 살펴본 Markov Decision Process와 Dynamic Programming에 이어, Monte Carlo Method를 살펴보자.

 

앞의 내용이 궁금하다면, 다음 링크를 참조하자.

 

https://jjuke-brain.tistory.com/68?category=957313 

Ch06. Markov Decision Process and Dynamic Programming (2)

 

OpenAI Gym을 사용한 실습은 아래 깃허브를 참조하자.

 

https://github.com/JJukE/ReinforcementLearning 

GitHub - JJukE/ReinforcementLearning: Reinforcement Learning Course

 

 

목차

 

 

 

 

 

1. Monte Carlo Methods

 

Monte Carlo 방법은 컴퓨터 공학을 포함하는 다양한 공학 과목 및 과학에서 널리 사용되는 알고리즘이다.

 

Reinforcement Learning에서는 특히 환경에 대한 정보가 없을 때 사용한다.

이전까지 배운 MDP, DP의 경우 환경에 대한 모델을 알고있다고 가정하고 강화 학습을 진행했었다.

다시 말해 이전까지 강화 학습은 model dynamics, 즉 transition probability \(P\), reward probability \(R\)에 대한 내용을 알고 있을 때 Bellman Equation을 풀어 Optimal Policy를 찾는 과정이었다.

하지만 이러한 모델에 대한 정보가 없다면, Monte Carlo 알고리즘을 사용하여 강화 학습을 진행해야 한다.

 

Monte Carlo 방법은 'Random Sampling'을 통해 근사해(Approximate Solutions)를 찾는다. 다시 말해, 여러 번 에피소드를 실행하여 나온 결과물을 통해 probability를 근사하는 것이다.

이는 샘플링을 통해 근사 답안을 찾는 통계적인 테크닉이다.

 

 

 

 

EX) Estimating the Value of \(\pi\) using Monte Carlo

 

예를 들어, 원주율 \(\pi\) 값을 Monte Carlo 방법으로 찾아보자.

 

Monte Carlo Example

 

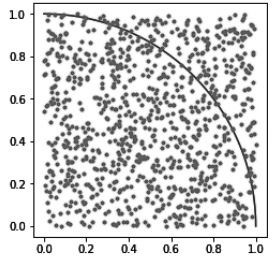
위 그림과 같이, '가로 1 × 세로 1'인 정사각형에 반지름이 1인 사분원이 존재한다.

이 상태에서 점을 랜덤하게 여러 개 찍으면, 위 사진과 같이 어떤 점은 사분원 안에, 어떤 점은 사분원 밖에 존재할 것이다.

 

그 후, 샘플링한 점들의 개수의 비를 통해 정사각형과 원의 넓이의 비를 근사화(approximate)할 수 있다.

$$ {Area \, of \, a \, circle \over Area \, of \, a \, square} = {No. \, of \, points \, inside \, the \, circle \over No. \, of \, points \, inside \, the \, square} $$

 

원의 넓이가 \(\pi r^2\)이고, 정사각형의 넓이가 \(a^2\)임을 알기 때문에, 넓이 비는 다음과 같이 나타낼 수 있다.

$$ {{1 \over 4} \pi r^2 \over a^2} = {No. \, of \, points \, inside \, the \, circle \over No. \, of \, points \, inside \, the \, square} $$

 

위 좌표계에서 \(r\)과 \(a\)가 1이므로, 대입하면 다음과 같은 결과를 얻는다.

$$ \pi = 4 * {No. \, of \, points \, inside \, the \, circle \over No. \, of \, points \, inside \, the \, square} $$

 

단계별로 \(\pi\)를 구하는 과정은 아래와 같다.

1. 정사각형 내에 랜덤하게 점을 찍는다.
2. \(x^2 + y^2 \le size\)식을 사용하여 원 내부의 점 개수를 계산한다.
3. 위 식을 사용하여 \(\pi\) 값을 구한다.

 

Sample의 수, 즉 랜덤 포인트의 수가 많아질수록 근사 값은 실제 값에 가까워질 것이다. (단, 계산 비용도 같이 커진다.)

즉, 이론적으로 표본을 무수히 많이 뽑는다면, 실제 값으로 Monte Carlo 방법의 결과를 사용할 수 있다.

 

 

 

 

2. Monte Carlo Prediction

 

그렇다면, Monte Carlo 방법을 강화 학습에 어떻게 적용시킬 수 있는지 알아보자.

 

먼저 이전에 배웠던 DP(Dynamic Programming)에서는 value iteration과 policy iteration을 사용하여 MDP(Markov Decision Process)를 푼다는 사실을 알고 있다.

value iteration과 policy iteration 둘 다 Optimal Policy \(\pi\)를 찾기 위해서는 transition probability, reward probability (model dynamics)를 알아야 한다.

 

하지만 Monte Carlo 방법에서는, state, action, reward의 Sample Sequence만 알면 강화 학습을 진행할 수 있다.

단, terminal state가 존재하는 episodic task에서만 적용 가능하다는 제한이 있다.

그리고, model-based learning인 DP와 달리 Monte Carlo는 모델이 필요 없으므로 model-free learning algorithm이다.

 

즉, 강화 학습에서 Monte Carlo 방법을 사용한다는 것은, 에피소드를 여러 번 샘플링하여 한 에피소드를 하나의 표본으로 생각하여 이 과정을 반복함으로써 근사화를 진행하는 것이다.

 

그리고, DP에서 optimal value function을 어떻게 정의하고, optimal policy를 어떻게 얻었는지 복기해보자.

DP에서는 value function \(V^\pi (s)\), 즉 policy \(\pi\)를 따를 때 해당 state에서 얻는 expected return 값을 사용한다.

value function의 값을 구하기 위해서는 \(\pi(s, a), P^a_{ss'}\) 값을 알아야 한다.

 

하지만 Monte Carlo 방법에서는 expected return (expected cumulative future discounted reward) 대신 mean return 값을 사용한다.

경험에 의해 episode 하나는 확실히 정해지므로, 평균을 바로 적용할 수 있는 것이다.

리턴 값이 많아질수록 (즉, 경험하는 episode가 많아질수록) 평균 값은 expected value로 수렴할 것이다.

 

따라서, Monte Carlo Prediction은 mean return 값을 취하여 value function을 근사화한다.

 

Monte Carlo Prediction의 단계를 살펴보자.

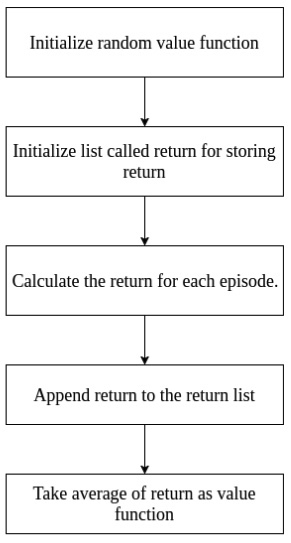
1. value function을 위한 랜덤 값을 초기화한다.
2. return을 저장하기 위한 빈 리스트를 초기화한다.
3. 각 에피소드마다 return을 계산한다.
4. 리스트에 계산한 return을 append한다.
5. return들의 평균 값을 value function으로 정한다.

 

Monte Carlo Prediction

 

여기서 Monte Carlo Prediction은 한 번 방문했던 state를 다시 방문할 때 return을 고려할지 안할지에 따라 두 가지로 나뉜다.

 

 

 

 

1) First Visit Monte Carlo Prediction

 

Value Function \(V^\pi (s)\)를 추정한다고 하자. state \(s\)의 값은 policy \(\pi\)에 존재하고, 주어진 에피소드의 집합은 \(\pi\)를 따르며 \(s\)를 거쳐간다.

이때, 에피소드 내에서 state \(s\)를 거쳐가는 것을 \(visit\) (방문한다)이라고 한다.

당연히 한 에피소드 내에서 같은 state \(s\)를 여러 번 방문할 가능성이 있다.

 

여기서 first visit MC prediction이란, 첫 번째 방문할 때에만 고려한다는 의미이다.

처음 방문 시에만 return을 리스트에 넣어주고, 두 번째 방문부터는 return을 리스트에 넣어주지 않는다.

 

pseudo code는 다음과 같다.

 

Input: a policy π to be evaluated
Initialize:
    V(s) ∈ R, arbitrarily,for all s ∈ S
    Returns(s) ← an empty list, for all s ∈ S

Loop forever (for each episode): # 한 에피소드에서
    Generate an episode following π: S_0, A_0, R_1, ... , S_{T-1}, A_{T-1}, R_T # states
    G ← 0
    Loop for each step of episode, t = T-1, T-2, ... , 0: # 각 state에서의 return
        G ← γG + R_{t+1}
        Unless S_t appears in S_0, S_1, ... , S_{t-1}: # 한 번도 방문하지 않았다면
            Append G to Reutrns(S_t)
            V(S_t) ← average(Returns(S_t))

 

 

 

 

2) Every Visit Monte Carlo Prediction

 

첫 번째 방문만 고려하는 first-visit Monte Carlo Prediction에 비해, every-visit Monte Carlo Prediction은 어떤 State를 방문하던 상관 없이 항상 Return을 리스트에 추가해주고, 평균을 구하는 데 사용한다.

 

First-visit Monte Carlo Prediction의 과정에서 \(S_t\)를 확인해주는 과정을 빼면 된다.

Pseudo code를 살펴보자.

 

Input: a policy π to be evaluated
Initialize:
    V(s) ∈ R, arbitrarily,for all s ∈ S
    Returns(s) ← an empty list, for all s ∈ S

Loop forever (for each episode): # 한 에피소드에서
    Generate an episode following π: S_0, A_0, R_1, ... , S_{T-1}, A_{T-1}, R_T # states
    G ← 0
    Loop for each step of episode, t = T-1, T-2, ... , 0: # 각 state에서의 return
        G ← γG + R_{t+1}
        # 모든 방문한 state s에 대해
        Append G to Reutrns(S_t)
        V(S_t) ← average(Returns(S_t))

 

first-visit MC와 every-visit MC 둘 다 에피소드 반복을 많이 할수록, 즉 visit의 수(또는 첫 visit의 수)가 많아질수록 (\(s\)가 무한에 가까워질수록) \(V^\pi (s)\)로 수렴한다.

 

first-visit MC라 가정하고, 이유를 살펴보자.

• 각 에피소드의 return은 서로 독립적(independent)이고, finite한 variance 값으로 항등 분포(identically distributed)를 따르며 \(V^\pi (s)\)를 추정한다. → iid
• 큰 수의 법칙(The law of large numbers, 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다, 즉 표본 수가 많을수록 모집단을 잘 반영한다.)에 의해 이러한 추정치의 평균은 기댓값에 수렴한다.
• 각 평균 값들은 unbiased estimate이고, 오차의 표준편차가 표본 수인 n에 대해 \(1/ \sqrt{n}\)까지 떨어진다.
  • 마지막 이유는 좀 더 깊은 통계학 지식을 요구하므로 알아만 두자.