나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다' 강의와 교재 내용을 공부하고, 그 내용을 정리한다.
(내용의 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 저'임을 사전에 밝힙니다.)
'Ch06. 최단 경로 알고리즘 (1)'에서 다익스트라 알고리즘을 살펴보았다. 이 포스팅에서는 또다른 최단 경로 알고리즘인 플로이드-워셜 알고리즘을 알아보자.
https://jjuke-brain.tistory.com/86?category=923173
Ch06. 최단 경로 알고리즘 (1) (feat. 이것이 취업을 위한 코딩테스트다)
나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다'강의와 교재 내용을 공부하고, 그 내용을 정리한다. (내용 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다 with
jjuke-brain.tistory.com
강의 영상은 다음과 같다.
https://www.youtube.com/watch?v=acqm9mM1P6o&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=16
목차
3. 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
플로이드 워셜 알고리즘은 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.
다익스트라 알고리즘과 마찬가지로 단계별로 거쳐가는 노드를 기준으로 알고리즘을 수행한다.
하지만 다익스트라 알고리즘과 달리, 매 단계마다 방문하지 않은 노드 중 최단 거리의 노드를 찾는 과정이 별도로 필요하지 않다.
대신 2차원 테이블에 최단 거리 정보를 저장하고, 점화식에 따라 갱신한다는 점에서 다이나믹 프로그래밍 유형에 속한다.
실제로 플로이드-워셜 알고리즘은 점화식에 맞게 3중 반복문을 사용하여 2차원 테이블을 갱신해준다. 구현 난이도는 다익스트라 알고리즘보다 쉽지만, 모든 노드에서 다른 모든 노드까지의 최단경로를 모두 계산하다 보니 시간 복잡도가 \(O(N^3)\)으로 매우 높다.
따라서 실제 문제풀이 과정에서는 노드 개수가 적은 상황에서 사용할 수 있으며, 노드와 간선의 개수가 많은 경우에는 다익스트라 알고리즘을 사용해야 하는 경우가 많다.
플로이드 워셜 알고리즘의 점화식은 다음과 같다.
$$ D_{ab} = \min (D_{ab}, D_{ak} + D_{kb}) $$
각 단계마다 특정 노드 k를 거쳐 가는 경우를 확인하는데,
점화식을 통해 a에서 b로 가는 최단 거리(기존 최단 거리)보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사한다.
즉, 기존 거리보다 k를 거쳐가는 거리가 더 짧은 경우 테이블의 값을 갱신하는 것이다.
1) 플로이드 워셜 알고리즘 동작 과정
[Step 0] 그래프를 준비하고, 최단 거리 테이블을 초기화한다.
단순히 각 노드가 다른 노드로 가는 비용을 테이블에 저장해준다.
[Step 1] 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다. (k = 1)
$$ D_{ab} = \min(D_{ab}, D_{a1} + D_{1b}) $$
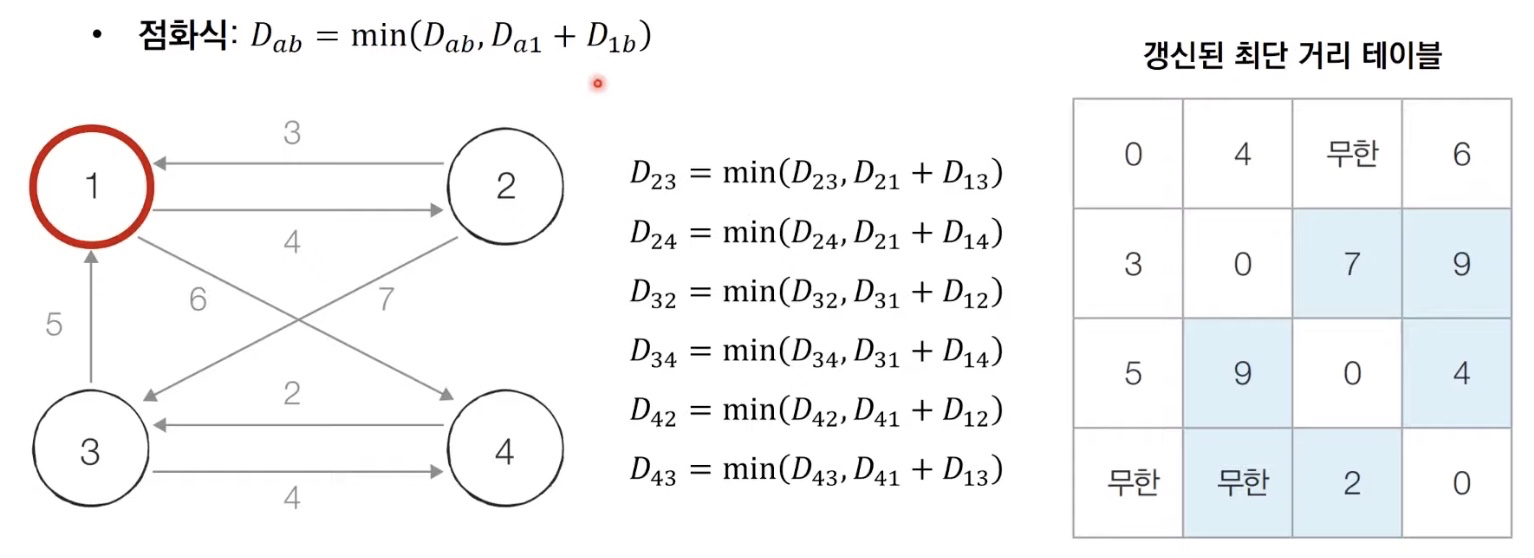
1번 노드를 (중간 지점으로) 거쳐 가는 경우를 표현하면 하늘색 표시된 부분처럼 6개(\(_{3}\mathrm{P}_{2}\))이다.
(자신을 제외한 노드들 중 2개를 고름)
[Step 2] 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다. (k = 2)
$$ D_{ab} = \min(D_{ab}, D_{a2} + D_{2b}) $$
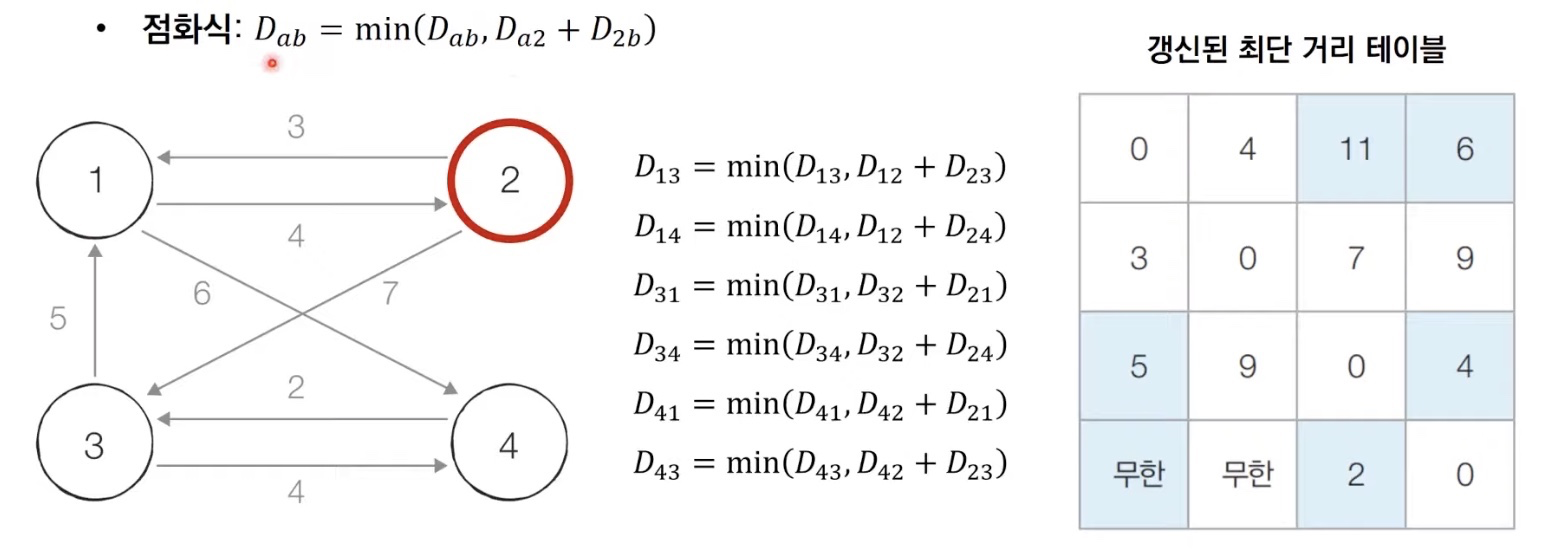
[Step 3, 4] 3번, 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
전체 과정을 k라는 변수를 통해 모든 노드를 하나의 step씩 진행하면, 최종적으로 3중 반복문으로 구현할 수 있게 된다.
2) 플로이드 워셜 알고리즘 구현
(1) Python 코드
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
# A에서 B로 가는 비용은 C라고 설정
a, b, c = map(int, input().split())
graph[a][b] = c
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 수행된 결과를 출력
for a in range(1, n + 1):
for b in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if graph[a][b] == 1e9:
print("INFINITY", end=" ")
# 도달할 수 있는 경우 거리를 출력
else:
print(graph[a][b], end=" ")
print()
3중 반복문에서, k는 거쳐가는 노드 (step을 진행할 노드), a는 출발 노드, b는 도착 노드를 의미한다.
(2) C++ 코드
#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M)
// 노드의 개수는 최대 500개라고 가정
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[501][501];
int main(void) {
cin >> n >> m;
// 최단 거리 테이블을 모두 무한으로 초기화
for (int i = 0; i < 501; i++) {
fill(graph[i], graph[i] + 501, INF);
}
// 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
if (a == b) graph[a][b] = 0;
}
}
// 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for (int i = 0; i < m; i++) {
// A에서 B로 가는 비용은 C라고 설정
int a, b, c;
cin >> a >> b >> c;
graph[a][b] = c;
}
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}
// 수행된 결과를 출력
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (graph[a][b] == INF) {
cout << "INFINITY" << ' ';
}
// 도달할 수 있는 경우 거리를 출력
else {
cout << graph[a][b] << ' ';
}
}
cout << '\n';
}
}
실제 플로이드 워셜 알고리즘을 사용할 때에는 노드 개수가 500을 넘지 않는 경우가 대부분이다.
3) 플로이드 워셜 알고리즘 성능 분석
노드의 개수가 \(N\)개일 때, 알고리즘 상으로 \(N\)번의 단계(Step)를 수행한다.
각 단계마다 \(O(N^2)\)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다.
따라서 플로이드 워셜 알고리즘의 총 시간복잡도는 \(O(N^3)\)이다.
코딩 테스트 시에 노드 개수가 500개만 되어도 500*500*500을 하게되면 1억이 넘어가는 수이므로, 시간 초과 판정을 받을 수 있다.
따라서 최단거리를 구해야 하는 문제가 출제된 경우 어떤 알고리즘을 사용하는 게 적절한지 고민해보고 적절한 알고리즘을 통해 문제를 해결해야 한다.
최근댓글