'Ch05. Markov Decision Process and Dynamic Programming (1)'에 이어서 내용을 정리해보자.
https://jjuke-brain.tistory.com/66
Ch05. Markov Decision Process and Dynamic Programming (1)
Markov Decision Process (MDP)는 강화학습 모델링의 기반이다. MDP는 문제의 정의, 즉 수식의 정의에 사용되고, Dynamic Programming은 iterative하게 equation을 푸는 방법을 제시한다. OpenAI Gym을 사용한 실..
jjuke-brain.tistory.com
OpenAI Gym을 사용한 실습은 아래 깃허브를 참조하자.
https://github.com/JJukE/ReinforcementLearning
GitHub - JJukE/ReinforcementLearning: Reinforcement Learning Course
Reinforcement Learning Course. Contribute to JJukE/ReinforcementLearning development by creating an account on GitHub.
github.com
4. Bellman Equation
Bellman Equation은 MDP로 모델링한 Reinforcement Learning 문제를 수식으로 나타낸 것이다.
1) Bellman Equation and Optimality
'MDP를 푼다'는 말은 'Optimal policy를 찾는다', 또는 'Optimal value function을 찾는다'라는 말과 같은 의미이다.
policy가 달라짐에 따라 수많은 서로 다른 value function들이 있을 수 있는데, 이중 optimal value function \(V^{*}(s)\)는 모든 다른 value function들보다 큰 값을 갖는 value function을 말한다. (보통 optimal을 *로 표현한다.)
이는 \(V^{\pi}(s)\)중 maximum 값을 갖는 \(\pi\)를 대입하였을 때의 \(V\)값으로, 다음 식으로 표현할 수 있다.
$$ V^{*}(s) = \underset{\pi}{\max}V^{\pi}(s) $$
또한, 모든 다른 value function들보다 큰 값을 갖는다는 의미는 곧 maximum return을 의미하는 것이기 때문에, optimal value function은 Q function의 maximum 값과 같다.
이를 수식으로 표현하면 다음과 같다.
$$ V^{*}(s) = \underset{a}{\max}Q^*(s, a) $$
이는 특정 state s에서 Q값이 maximum이 되는 a를 선택했을 때의 value를 말한다.
Ref. \(\max\) vs \(\operatorname{argmax}\)
참고로, \(\max\) 와 \(\operatorname{argmax}\)의 차이점을 알아둘 필요가 있다.
$$ y = f(x)에서 \begin{cases} \underset{x}{\max}f(x), & y \mbox{가 최대인} f(x) \mbox{값} \\ \underset{x}{\operatorname{argmax}}f(x), & y \mbox{가 최대가 되도록 하는 } x \mbox{값} \end{cases} $$
Ref. Expectation (\(\mathbb{E}\)), 기댓값
확률 변수의 기댓값이란, 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값이다.
좀 더 쉽게말하자면, 각 사건에 대한 (값 * 확률)들을 모두 더한 값이다.
또한 선형 연산자이기 때문에 가산성과 동차성이 성립한다.
$$ \mathbb{E}(X + Y) = \mathbb{E}(X) + \mathbb{E}(Y) $$
$$ \mathbb{E}(cX) = c\mathbb{E}(X) $$
(단, c는 상수)
2) Bellman Equation for the Value Function
먼저 Value Function, 즉 state s에 존재하는 것이 얼마나 이득인지의 값에 대한 Bellman Eqn이다. 다음 유도과정을 살펴보자.
$$ \begin{align*} V^{\pi}(s) &= \mathbb{E}_\pi [R_t | s_t = s] \\ &= \mathbb{E}_\pi [r_{t+1} + \gamma R_{t+1} | s_t = s] \\ &= \mathbb{E}_\pi [r_{t+1} | s_t = s] + \mathbb{E}_\pi [\gamma R_{t+1} | s_t = s] \\ &= \mathbb{E}_\pi [r_{t+1} | s_t = s] + \gamma \mathbb{E}_\pi [R_{t+1} | s_t = s] \\ &= \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum}P^a_{ss'}R^a_{ss'} + \gamma \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum}P^a_{ss'}V^\pi(s') \\ &= \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum}P^a_{ss'} [R^a_{ss'} + \gamma V^\pi(s')] \end{align*} $$
각 수식이 다음 줄의 수식으로 어떻게 전개되는지 분석해보자.
- return의 recursive representation
- 기댓값의 가산성
- 기댓값의 동차성
- 기대값을 두 번 연쇄적으로 구하는 개념이다.
- \( \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum} P^a_{ss'}R^a_{ss'} \)의 계산
- \( P^a_{ss'}R^a_{ss'} \)는 기대값 계산에 있어 '확률 × 값'을 나타낸다. 이렇게 s'에 대해 기대값을 구한 \( \underset{s'}{\sum}P^a_{ss'}R^a_{ss'} \) 자체가 값이고, \( \pi(s, a) \)가 a를 선택할 확률의 의미를 가지며 이 둘의 곱이 전체 기댓값의 계산과정이다.
- 뒤에 더해지는 과정도 똑같다. 두 번의 기댓값을 연쇄적으로 계산한 후, \( \gamma \)를 곱해주어 더한다.
- \( \underset{a}{\sum} \pi(s, a) \underset{s'}{\sum} P^a_{ss'}R^a_{ss'} \)의 계산
- s'에 대한 summation에서 공통 인자인 P^a_{ss'}를 기준으로 묶는다.
결론적으로 얻는 식은 다음과 같다.
$$ V^\pi(s) = \underset{a}{\sum}\pi(s, a) \underset{s'}{\sum} P^a_{ss'} [R^a_{ss'} + \gamma V^\pi(s')] $$
여기서, 헷갈릴 수 있는 항을 간단히 설명한다.
- \( P^a_{ss'} \) : state s에서 state s'으로 a action을 통해 transition할 확률 (transition probability)
- \( R^a_{ss'} \) : state s에서 state s'으로 a action을 통해 transition할 때, agent가 받을 것으로 예상되는(expected) reward
- \( \pi(s, a) \) : state s에서 a action을 선택할 확률
- \( \gamma V^\pi(s') \) : expected next state
수식을 분석해보자.
먼저, 현재 state s에서의 Value Function을 구하는 데, 마지막에 정리된 수식을 보면 마지막 항에 다음 state s'에서의 Value Function이 포함되어 있다.
이는 계산이 뒤에서부터, recursive하게 진행된다는 것을 알 수 있다.
아래와 같은 Backup Diagram을 통해 쉽게 이해해보자.

root node인 s state부터 시작하여 \( \pi \)를 통해 action set 중 하나를 선택하고, 각 a에 대해 environment가 다음 state s'중 하나에 응답하며 reward r을 받는다. 이때 r은 probability p에의해 결정된다.
Bellman Equation에서는 모든 가능성에 대해 평균(기댓값)을 구하고, 각각이 일어날 확률에 대해 weight를 부여한다.
이는 곧 start state s에서의 값이 next state의 기댓값과 reward의 기댓값의 합과 같음을 의미한다.
3) Bellman Equation for the Q function
다음으로, Q function, 즉 현재 state s에서 action a가 얼마나 좋은지의 값에 대한 Bellman Eqn을 살펴보자.
유도과정은 value function에서와 비슷하므로 간단히 표현하겠다.
$$ \begin{align*} Q^\pi(s, a) &= \mathbb{E}[R_t | s_t = s, a_t = a] \\ &= \underset{s'}{\sum}P^a_{ss'} [ R^a_{ss'} + \gamma \underset{a'}{\sum} \pi(s', a') Q^\pi(s', a')] \end{align*} $$
정리하면 다음과 같다.
$$ Q^\pi(s, a) = \underset{s'}{\sum}P^a_{ss'} [ R^a_{ss'} + \gamma \underset{a'}{\sum} \pi(s', a') Q^\pi(s', a')] $$
backup diagram은 다음과 같이 표현된다.
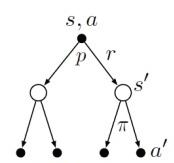
여기서 value function에서의 backup diagram 및 eqn과 비교해 보았을 때, \( \pi(s,a) \) 항이 사라진 것을 알 수 있는데, 이는 Q function 자체가 action의 선택에 대한 개념도 포함하기 때문이다.
4) Bellman Optimality Equation
Bellman Optimality Eqn을 푸는 것이 곧 optimal policy를 찾는 것이며, 강화학습의 최종 목적이다.
앞서 언급한 Bellman Eqn의 optimality 성질에 따라 다음과 같이 나타낼 수 있다.
$$ \begin{align*} V^*(s) &= \underset{\pi}{\max} V^\pi(s) = \underset{a}{\max} Q^*(s, a) \\ &= \underset{a}{\max} \underset{s'}{\sum} P^a_{ss'} [R^a_{ss'} + \gamma V^*(s')] \\ &= \underset{a}{\max} \underset{s'}{\sum} P^a_{ss'} [R^a_{ss'} + \gamma \underset{a'}{\sum} Q^\pi(s', a')] \end{align*} $$
두 번째 줄은 value function, 세 번째 줄은 Q function을 기준으로 정의한 것이다.
5. Dynamic Programming (DP)
Dynamic Programming은 Optimal value function을 찾기 위한, 즉 optimal policy를 계산하기 위한 알고리즘을 말한다. 단, 이때 environment의 perfect model(모델의 state, action, reward, transition prob 등을 모두 아는 모델)이 주어져야 하고, 이는 Markov Property를 따라야 한다.
보통 environment는 끝이 정해진 MDP로 둔다. 즉 set, action, reward set들을 각각 \(S\), \(A\), \(R^a_{ss'}\)으로 두는데, 이들은 모두 finite하고, 이들의 흐름은 transition probabiltiy \(P^a_{ss'}\)을 따른다.
optimal policy를 찾기 위해서는 Bellman optimality equation을 푸는데, 이를 위해 Dynamic Programming이라는 방법을 사용하는 것이다.
DP에서는 복잡한 문제를 한 번에 풀기보다, 간단한 sub-problem으로 나누어 각각의 해를 찾은 뒤 iterative하게 solution을 계산 및 저장한다.
이때 같은 sub-problem이 발생하면 다시 계산할 필요 없이 저장해둔 solution을 사용한다.
Bellman Equation을 푸는 두 가지 강력한 알고리즘은 다음과 같다.
- Value Iteration
- Policy Iteration
1) Value Iteration
말그대로 Value를 기준으로 iteration이 진행되는 알고리즘을 말한다.
value iteration을 처음 시작할 때, random value function을 사용한다. 이는 optimal value function이 아닐 것이며, optimal value function을 찾을 때까지 반복적으로 improved value function으로 갱신하는 방식을 사용한다.
optimal value function을 찾으면 이로부터 쉽게 optimal policy를 찾을 수 있을 것이다.
value iteration에 대한 수식과 flow chart는 아래와 같다.
$$ \begin{align*} V^*(s) &= \underset{\pi}{\max} V^\pi(s) = \underset{a}{\max} Q^*(s, a) \\ &= \underset{a}{\sum} P^a_{ss'} [R^a_{ss'} + \gamma V^*(s')] \end{align*} $$

Flow chart는 다음과 같은 흐름을 갖는다.
- random value function, 즉 각 state의 random value를 초기화한다.
- Q function을 계산한다.
- value function을 갱신한다. 이때 값은 Q function 값의 최대값을 갖도록 한다.
- 2., 3. 과정을 value function의 차이가 매우 작아질 때까지 반복한다. (작다는 기준 : hyperparameter)
EX)
예시를 통해 알아보자.
다음과 같은 간단한 grid가 존재한다.
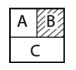
현재 상태는 A이고, 목표는 B에 들르지 않고 C에 도착하는 것이다.
action은 두가지로, 0은 왼쪽 또는 오른쪽 이동, 1은 위쪽 또는 아래쪽 이동이다.
이를 DP 알고리즘으로 푼다면 아래와 같은 과정으로 풀 수 있다.
먼저, 모든 state에 대해 random value를 배정한다. 이는 곧 random value function을 초기화하는 것이다.
모든 값을 0으로 배정한다고 해보자.
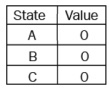
그다음, 모든 (state, action) pair에 대해 Q value를 계산한다.
$$ Q(s, a) = \subset{s'}{\sum} P^a_{ss'} [R^a_{ss'} + \gamma V(s')] $$
물론 이를 계산하려면 transition probability(\(P\)), reward probability(\(R\))를 알아야 한다.
state A에 대해 \(P\), \(R\)을 아래와 같이 가정하고, \(\gamma = 1\)로 둔다고 하자.

식에 따라 계산하면 \(Q(A, 0) = -0.1\), \(Q(A, 1) = 0.3\) 이 나올 것이다.
이러한 계산결과를 아래와 같이 Q table에 갱신시킨다.

Q 값의 최대 값으로 해당 State의 value function을 갱신시킨다.

이와 같은 과정을 B, C state에도 반복적으로 적용하여 첫 번째 iteration을 돈 결과는 다음과 같다.

'Q function의 계산 → Q table 갱신 → value function 갱신' 과정을 value들의 차이가 매우 작아질 때까지 반복한다.


2와 3에서의 차이가 매우 비슷하다고 하자. (실제 적용 시 threshold라는 hyperparameter를 정해야 함)
이제 optimal value function을 구했는데, 이로부터 optimal policy를 얻어야 하는데, 마지막 value function (optimal value function)에서 Q function을 한 번 더 계산하였을 때 가장 큰 값이 바로 optimal policy이다.

2) Policy Iteration
value iteration과 달리, policy iteration에서는 random policy를 초기화한다.
이후 그 policy에 해당하는 value function을 찾고, optimal policy가 될 때까지 policy를 갱신한다.
policy iteration에서 Flow Chart는 다음과 같다.

policy iteration의 경우, 특별한 두 가지 step이 있다.
하나는 Policy Evaluation으로, 랜덤으로 추정된 policy의 value function을 평가하는 것이다.
다른 하나는 Policy Improvement로, value function의 평가 시 optimal이 아니면 improved policy를 찾는 것이다.
Flow Chart의 과정을 자세히 살펴보자.
- random policy를 초기화한다.
- policy에 따라 value function을 계산하고, 그 policy가 optimal한지 policy evaluation을 진행한다.
- optimal이 아니라면, 새로운 policy를 찾아 policy improvement를 진행한다.
- optimal policy를 찾을 때까지 2., 3. 과정을 반복한다.
EX)
value iteration에서의 예제를 그대로 policy iteration에 적용해보자.
먼저, random policy function을 초기화한다.
이는 각 state에 random action을 부여하여 진행한다.
$$ \begin{align*} & A \rightarrow 0 \\ & B \rightarrow 1 \\ & C \rightarrow 0 \end{align*} $$
다음으로, 초기화한 policy에 대한 value function을 계산한다.

그렇다면, 새로운 policy는 어떻게 계산해야할까?
이는 value iteration에서와 비슷하다. 새로운 value function에 대해 Q function을 계산한 후에 각 state별로 maximum value를 갖는 action을 새로운 policy로 취하면 된다.
여기서 만약 새로운 policy가 생성되었는데, 이전 policy와 같다면 수렴한 것이므로 이것이 optimal policy이다.
이전 policy와 다르다면 이전 과정을 반복한다.
pseudo code는 다음과 같다.
policy_iteration():
Initialize random policy
for i in num_of_iter:
Q_val = value_function(random_policy)
new_policy = Maximum (s, a) pair from Q_val
if random_policy == new policy:
break
random_policy = new_policy
return policy
6. Solving the Frozen Lake Problem using Value Iteration and Policy Iteration
실습 내용은 github를 참조하도록 한다.
https://github.com/JJukE/ReinforcementLearning/blob/main/5_1%20Frozen%20Lake%20Problem.ipynb
GitHub - JJukE/ReinforcementLearning: Reinforcement Learning Course
Reinforcement Learning Course. Contribute to JJukE/ReinforcementLearning development by creating an account on GitHub.
github.com








최근댓글