나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다'강의와 교재 내용을 공부하고, 그 내용을 정리한다.
(내용의 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 저'임을 사전에 밝힙니다.)
'Ch03. 정렬 알고리즘'에 이어, 이진 탐색 알고리즘에 대해 알아볼 것이다. 정렬 알고리즘이 궁금하다면 아래 링크를 참조하자.
https://jjuke-brain.tistory.com/71
Ch03. 정렬 알고리즘 (feat. 이것이 취업을 위한 코딩테스트다) (1)
나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다'강의와 교재 내용을 공부하고, 그 내용을 정리해본다. (내용의 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다
jjuke-brain.tistory.com
https://jjuke-brain.tistory.com/72
Ch03. 정렬 알고리즘 (feat. 이것이 취업을 위한 코딩테스트다) (2)
나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다'강의와 교재 내용을 공부하고, 그 내용을 정리한다. (내용의 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다 wi
jjuke-brain.tistory.com
강의 영상 링크는 다음과 같다.
https://www.youtube.com/watch?v=94RC-DsGMLo&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=5
목차
1. 이진 탐색 알고리즘
탐색이란, 리스트 내에서 데이터를 찾는 것을 말한다.
탐색 방법에는 크게 순차 탐색, 이진 탐색이 있다.
순차 탐색은 리스트 안에 있는 특정 데이터를 찾기 위해 단순히 앞에서부터 하나씩 확인하는 방법이고,
이진 탐색은 정렬된 리스트에서 특정한 데이터를 빠르게 탐색할 수 있는 알고리즘이다.
따라서 이진 탐색은 로그의 시간 복잡도를 갖는다.
이진 탐색을 수행할 때에는 탐색 범위를 명시해주어야 하는데, '시작점, 끝점, 중간점' index를 이용한다.
1) 이진 탐색 동작 예시
다음 예시를 살펴보자.
이미 정렬된 10개의 데이터 중에서 값이 4인 원소를 찾고자 한다.

[Step 1] 시작점 : 0(index), 끝점 : 9, 중간점 : 4 (보통 소수점 이하는 제거한다.)

중간점에 위치하는 값인 8과 찾고자하는 값인 4를 비교하여, 중간점 값보다 작으면 왼쪽만, 크면 오른쪽만 확인하면 된다.
중간점 값이 시작점 값보다 크므로, 중간점을 끝점으로 옮긴다.
[Step 2] 시작점: 0, 끝점: 3, 중간점: 1
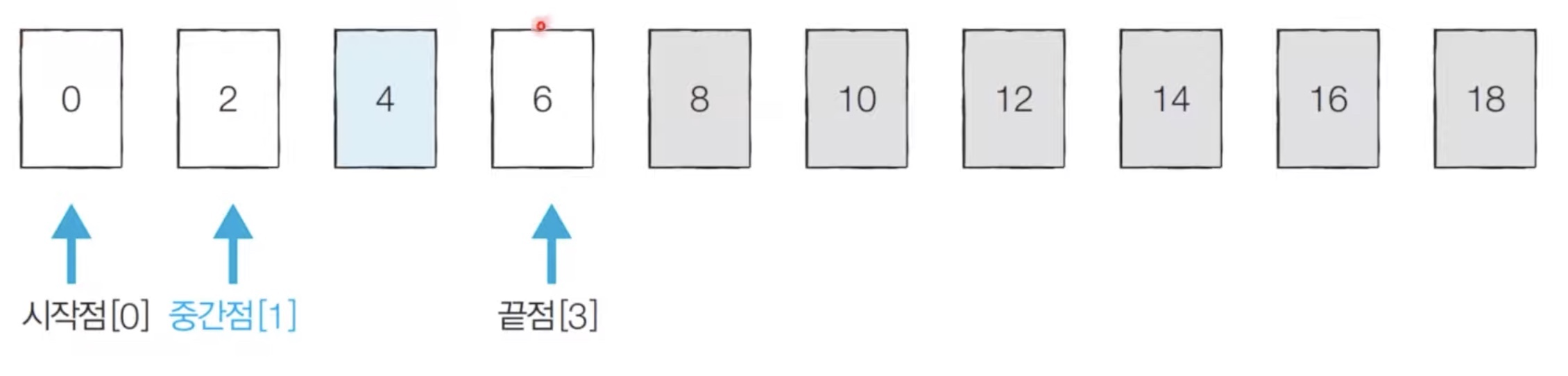
따라서 위와 같이 범위가 좁혀졌다.
이번에는 중간점 위치보다 찾는 값이 크므로, 중간점을 시작점으로 옮긴다.
[Step 3] 시작점: 2, 끝점: 3, 중간점: 2
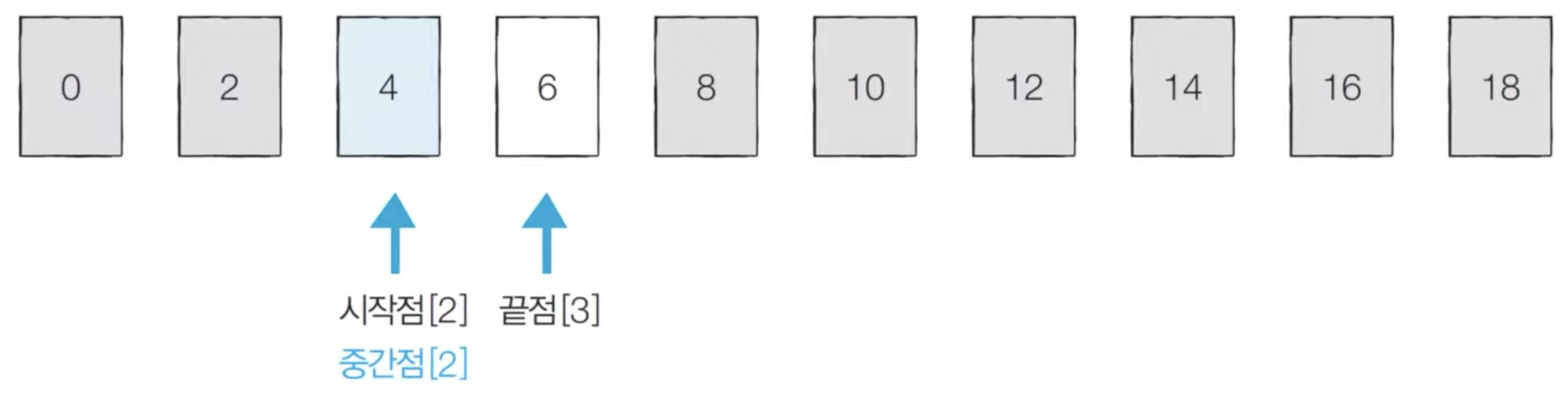
여기서 중간점 위치의 값이 찾는 값이므로 탐색 과정을 마친다.
데이터를 모두 탐색하는 것보다 이진 탐색을 사용하면 탐색 범위가 빠르게 줄어들어 시간 복잡도 측면에서 유리하다.
2) 이진 탐색 시간 복잡도
단계마다 탐색 범위를 2로 나누는 것과 동일하므로, 연산 횟수는 \( \log_{2} N) 에 비례한다.
예를 들어 초기 데이터 개수가 32개일 때 이상적으로 1단계를 거치면 16개, 2단계를 거치면 8개, 3단계를 거치면 4개, ... 와 같이 탐색할 데이터의 개수가 줄어든다.
따라서 이진 탐색은 탐색 범위를 절반씩 줄여, 시간 복잡도는
3) 이진 탐색 코드
(1) 이진 탐색 Python 코드
먼저 재귀함수를 활용한 파이썬 코드를 살펴보자.
import sys
fin = sys.stdin.readline
# 재귀함수로 이진 탐색 구현
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2 # 소수점 버림
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid + 1, end)
# n(원소 개수)과 target(찾고자 하는 값) 입력 받기
n, target = list(map(int, fin().split()))
# 전체 원소 입력 받기
array = list(map(int, fin().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
이진 탐색 과정을 잘 이해했다면 쉽게 코드를 이해할 수 있을 것이다.
다음으로, 반복문으로 이진 탐색을 구현한 파이썬 코드이다.
import sys
fin = sys.stdin.readline
# 이진 탐색 소스코드 구현 (반복문)
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
end = mid - 1
else:
start = mid + 1
return None
n, target = map(int, fin().split())
array = list(map(int, fin().split())
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.)
else:
print(result + 1)
반복문으로 구현할 경우 끝점 또는 시작점을 상황에 따라 바꿔주며 구현한다.
(2) 이진 탐색 C++ 코드
#include <bits/stdc++.h>
using namespace std;
int binarySearch(vector<int>& arr, int target, int start, int end) {
while (start <= end) {
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) return mid;
// 중간점 값보다 찾는 값이 작은 경우 왼쪽 확인
else if (arr[mid] > target) end = mid - 1;
// 중간점 값보다 찾는 값이 큰 경우 오른쪽 확인
else start = mid + 1;
}
return -1;
}
int n, target;
vector<int> arr;
int main(void) {
// n(원소의 개수)과 target(찾는 값)을 입력받기
cin >> n >> target;
// 전체 원소 입력 받기
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
cout << "원소가 존재하지 않습니다." << endl;
}
else {
cout << result + 1 << endl;
}
return 0;
}
C++ 코드는 반복문 구현만 소개하도록 한다.
로직은 파이썬과 똑같으며, 특이한 점은 vector(array) 입력을 받을 때에 &를 사용하여 reference를 입력으로 받는다는 것이다.
만약 &를 빼면 함수를 호출할 때 vector에 담겨 있던 값들을 copy하기 때문에
2. 파이썬 이진 탐색 라이브러리
추가적으로, 코딩 테스트 문제를 풀 때 이진 탐색과 관련한 유용한 라이브러리가 있다.
바로 'bisect_left(a, x)'와 'bisect_right(a, x)'이다.
- bisect_left(a, x) : 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인덱스를 반환한다. C++에서의 'lower_bound()'와 같다.
- bisect_right(a, x) : 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환한다. C++에서의 'upper_bound()'와 같다.
예를 들어, 다음과 같이 정렬된 리스트 a가 있다고 하자.
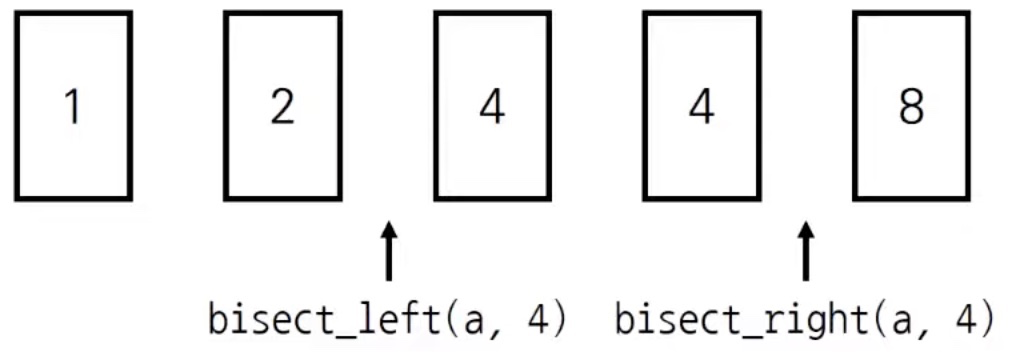
여기서 같은 값 4의 개수에 따라 bisect_left(a, 4)결과와 bisect_right(a, 4)의 차가 달라진다.
1) 값이 특정 범위에 속하는 데이터의 개수 구하기
위와 같은 특징을 사용하여 값이 특정 범위에 속하는 데이터의 개수를 구할 수 있다.
from bisect import bisect_left, bisect_right
# 값이 [left_val, right_val]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_val, right_val):
right_idx = bisect_right(a, right_val)
left_idx = bisect_left(a, left_val)
return right_idx - left_idx
# 배열 선언
a = [1, 2, 3, 3, 3, 3, 4, 4, 8, 9]
# 값이 4인 데이터 개수 출력
print(count_by_range(a, 4, 4))
# 값이 [-1, 3] 범위에 있는 데이터 개수 출력
print(count_by_range(a, -1, 3))
2) Parametric Search
코딩 테스트에서 이진 탐색 문제가 출제될 경우, parametric search 유형의 문제가 출제되는 경우가 많다. (즉, 코딩 테스트에서 parametric search 문제는 이진 탐색을 이용하여 해결할 수 있다.)
Parametric search란, 최적화 문제(최적 해를 찾는 문제)를 결정 문제(yes or no)로 바꾸어 해결하는 기법이다.
최적화 문제란 어떤 함수의 값을 가능한 낮추거나 최대한 높이는 등의 문제를 말한다.
최적화 문제는 바로 해결하기가 어려운 경우가 많은데, 그 문제를 여러 번의 결정 문제로 문제 형태를 바꾸어 해결할 수 있는 경우가 있다.
예를 들어, 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제를 생각해보자.
탐색 범위를 좁혀 가면서 현재 범위에서 이 조건을 만족하는지 체크하여 그 여부에 따라 탐색 범위를 좁혀 가며 가장 알맞은 값을 찾을 수 있다.
3. 이진 탐색 예제 - 떡볶이 떡 만들기
Q) 여행가신 부모님을 대신하여 떡집 일을 하기로 했다. 오늘은 떡볶이 떡을 만드는 날이다. 떡볶이 떡은 길이가 일정하지 않다. 대신에 한 봉지 안에 들어가는 떡의 길이는 절단기로 잘라서 맞춰준다.
절단기에 높이 H를 지정하면 줄지어진 떡을 한번에 절단한다. 높이가 H보다 긴 떡은 H 윗부분이 잘릴 것이고, 낮은 떡은 잘리지 않을 것이다.
예를 들어, 높이가 19, 14, 10, 17cm인 떡이 나란히 있고, 절단기 높이를 15cm로 지정하면 자른 뒤 떡의 높이는 15, 14, 10, 15cm가 될 것이다. 잘린 떡의 길이는 차례대로 4, 0, 0, 2cm이다. 손님은 6cm만큼의 길이를 가져간다.
손님이 왔을 때 요청한 총 길이가 M일때, 적어도 M만큼의 떡을 얻기 위해 절단기에서 설정할 수 있는 높이 H의 최댓값을 구하는 프로그램을 작성하시오.
문제 조건은 다음과 같다.
- 입력 조건
- 첫째 줄에 떡의 개수 N과 요청한 떡의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
- 둘째 줄에는 떡의 개별 높이가 주어진다. 떡 높이의 총합은 항상 M 이상이므로, 손님은 필요한 양만큼 떡을 사갈 수 있다. 높이는 10억보다 작거나 같은 양의 정수 또는 0이다.
- 출력 조건
- 적어도 M만큼의 떡을 집에 가져가기 위해 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
- 입력 예시
- 4 6
- 19 15 10 17
- 출력 예시
- 15
1) 문제 해결 아이디어
적절한 높이를 찾을 때까지 이진 탐색을 수행하여 높이 H를 반복하여 조정하면 된다.
'현재 이 높이로 자르면 조건을 만족할 수 있는가?'를 확인하여 조건의 만족 여부(yes or no)에 따라 탐색 범위를 좁혀서 해결할 수 있다.
예를 들어 조건을 만족할 수 없다고 한다면, H를 낮추어 더 많은 양의 떡이 잘릴 수 있도록 해야 할 것이다.
절단기의 높이는 0부터 10억까지의 정수 중 하나인데, 이와 같이 큰 탐색 범위를 보면 '이진 탐색'을 떠올릴 수 있어야 한다.
탐색 범위가 매우 큰 경우 순차 탐색을 진행하면 시간 초과가 뜰 확률이 높기 때문이다.
문제에서 제시된 예시를 통해 그림으로 이해해보자.
[Step 1] 시작점: 0, 끝점: 19, 중간점: 9 → 이때 필요한 떡의 크기 M = 6
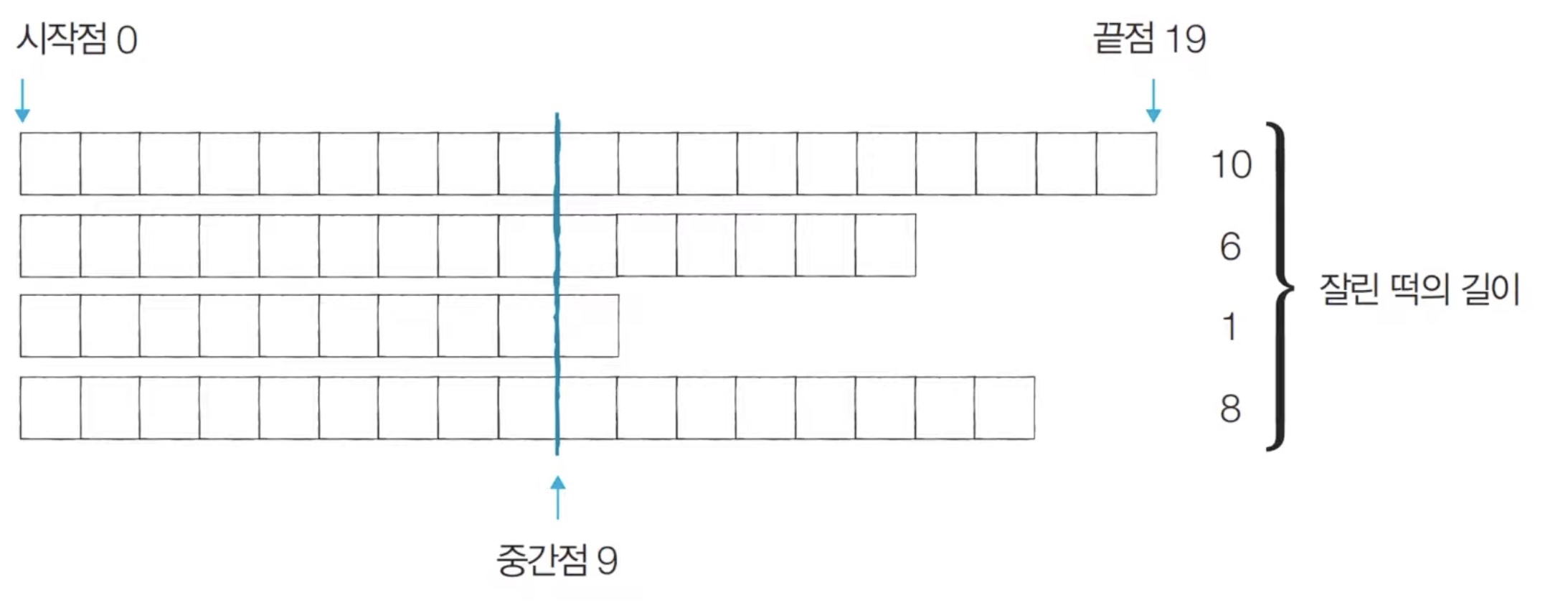
여기서 잘린 떡의 길이의 합은 25이고, 이는 필요한 떡의 길이 M보다 크므로 결과를 저장하고 '중간점 + 1'을 시작점으로 두어 H를 높여본다.
[Step 2] 시작점: 10, 끝점: 19, 중간점: 14 → M = 6
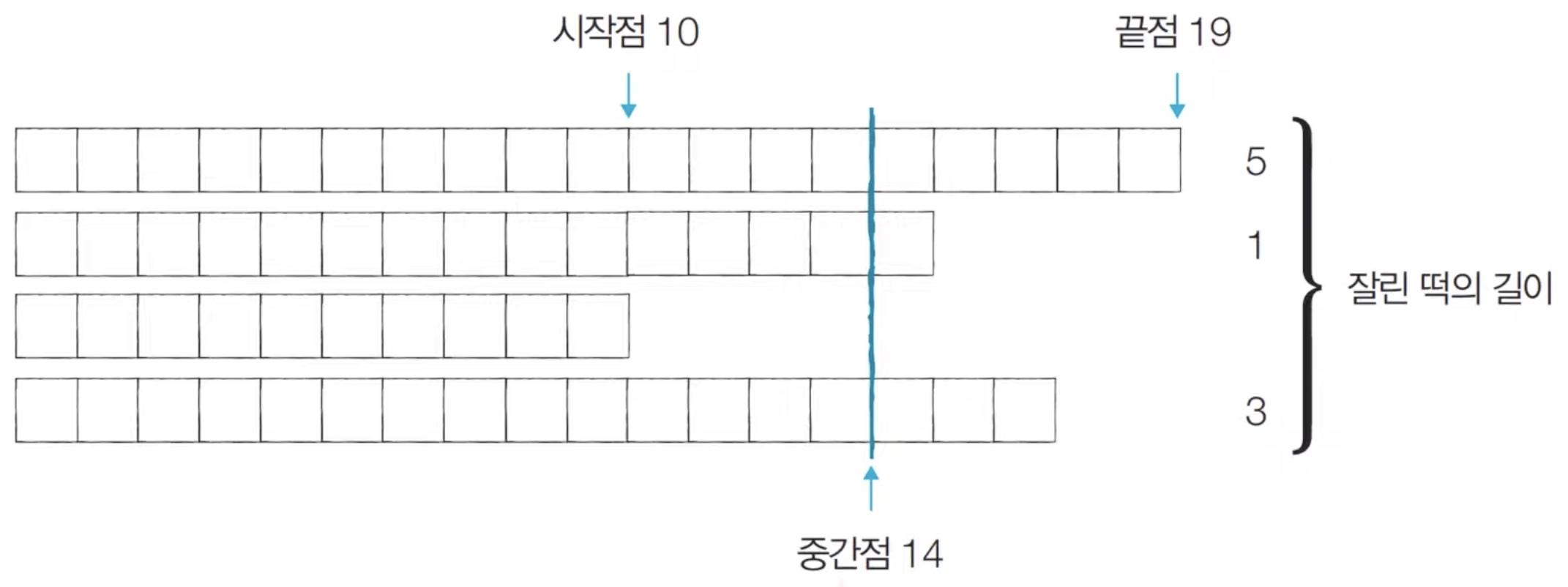
여기서 또한 잘린 떡의 길이의 합이 9로 M보다 크므로, 결과를 저장하고 '중간점 + 1'을 시작점으로 두어 H를 높여본다.
[Step 3] 시작점: 15, 끝점: 19, 중간점: 17 → M = 6
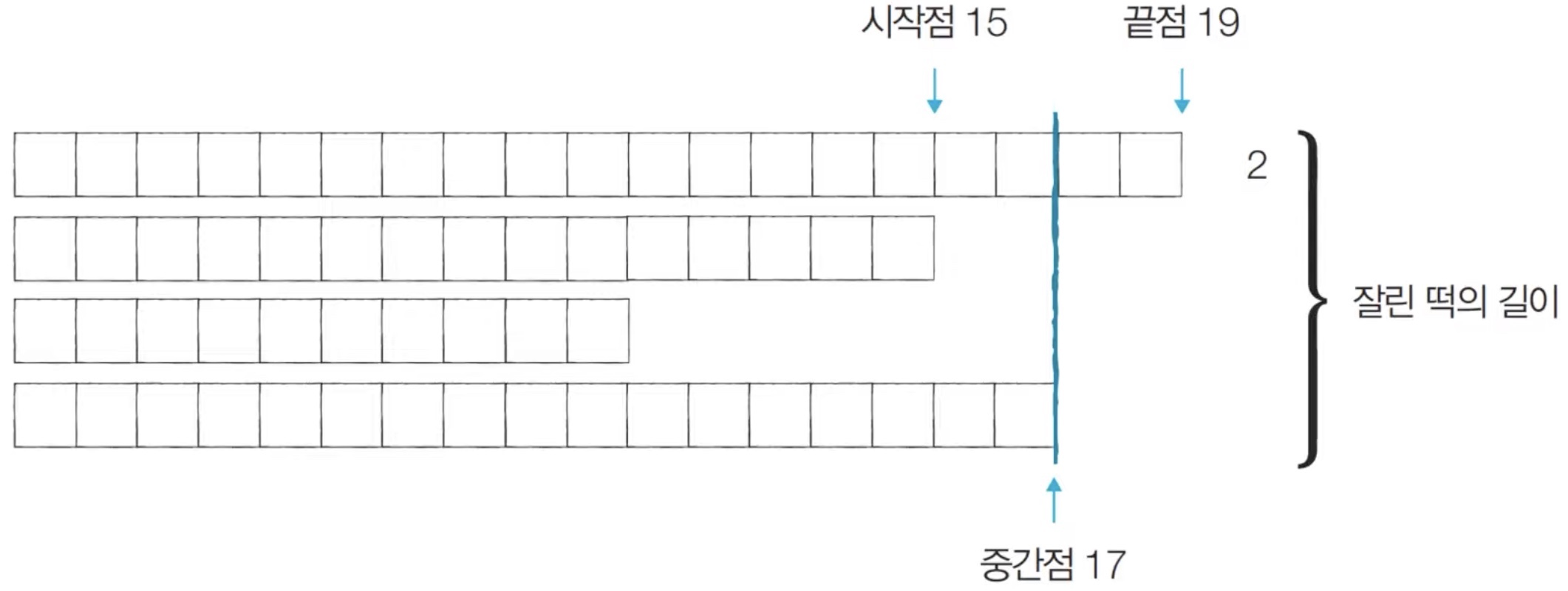
잘린 떡의 길이 합이 2로 M보다 작으므로, 결과를 저장하지 않고 '중간점 - 1'을 끝점으로 두어 H를 낮춘다.
[Step 4] 시작점 : 15, 끝점: 16, 중간점: 15 → M = 6
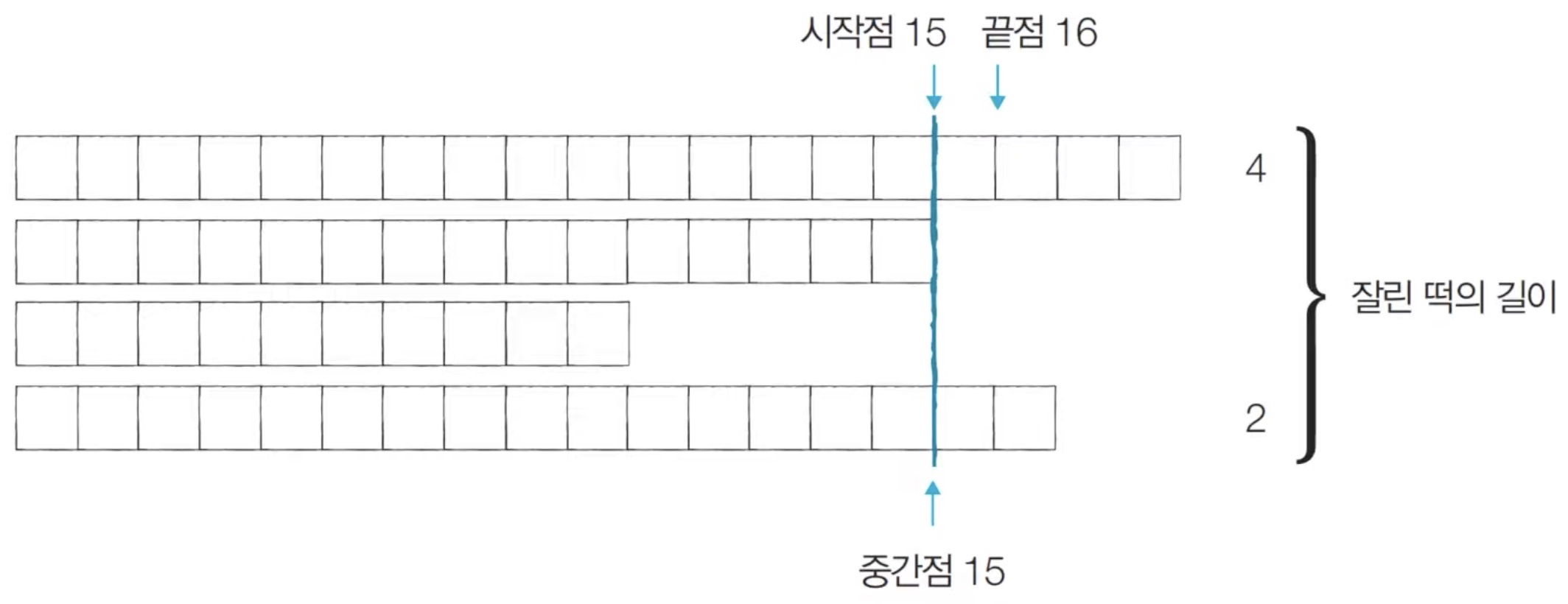
잘린 떡의 길이 합이 6으로 M과 같으므로 결과를 저장하고, 더 이상 탐색 범위를 줄일 수 없으므로 최종 답으로 정한다.
이렇게 이진 탐색 과정을 반복하면 답을 도출할 수 있다.
중간점의 값은 시간이 지날수록 최적화된 값이 되기 때문에, 과정을 반복하면서 얻을 수 있는 떡의 길이의 합이 필요한 떡의 길이보다 크거나 같을 때마다 중간점의 값을 기록하면 된다.
2) Code
(1) Python
import sys
fin = sys.stdin.readline
# 떡의 개수(N)와 요청한 떡의 길이(M)를 입력
n, m = map(int, fin().split())
# 각 떡의 개별 높이 정보 입력
array = list(map(int, fin().split()))
# 이진 탐색을 위한 시작점과 끝점 설정
start = 0
end = max(array)
# 이진 탐색 수행 (반복문)
result = 0
while(start <= end):
total = 0
mid = (start + end) // 2
for x in array:
# 잘랐을 때의 떡의 양 계산
if x > mid:
total += x - mid
# 떡의 양이 부족한 경우 더 많이 자르기 (왼쪽 부분 탐색, 높이를 줄임)
if total < m:
end = mid - 1
# 떡의 양이 충분한 경우 덜 자르기 (오른쪽 부분 탐색, 높이를 높임)
else:
result = mid # 최대한 덜 잘랐을 때가 정답이므로, 여기에서 기록
start = mid + 1
print(result)
아이디어를 잘 이해했다면 쉽게 코드를 이해할 수 있을 것이다.
(2) C++
#include <bits/stdc++.h>
using namespace std;
// 떡의 개수(N)와 요청한 떡의 길이(M)
int n, m;
// 각 떡의 개별 높이 정보
vector<int> arr;
int main(void) {
cin >> n >> m;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
// 이진 탐색을 위한 시작점과 끝점 설정
int start = 0;
int end = 1e9; // 일단 가장 큰 값 부여
// 이진 탐색 수행 (반복적)
int result = 0;
while (start <= end) {
long long int total = 0; // 최대 10억까지 저장할 수 있어야 하므로 long long 자료형 사용
int mid = (start + end) / 2;
for (int i = 0; i < n; i++) {
// 잘랐을 때 떡의 양 계산
if (arr[i] > mid) total += arr[i] - mid;
}
if (total < m) { // 떡의 양이 부족한 경우 더 많이 자르기 (왼쪽 부분 탐색, H를 낮춤)
end = mid - 1;
}
else { // 떡의 양이 충분한 경우 덜 자르기 (오른쪽 부분 탐색, H를 높임)
result = mid;
start = mid + 1;
}
}
cout << result << endl;
}
로직은 파이썬과 같다.
4. 정렬된 배열에서 특정 수의 개수 구하기
N개 원소를 포함하는 수열이 오름차순으로 정렬되어 있다. 이때 이 수열에서 x가 등장하는 횟수를 계산하라. 예를 들어 수열 {1, 1, 2, 2, 2, 2, 3}이 있을 때, x = 2라면, 현재 수열에서 값이 2인 원소가 4개이므로 4를 출력한다.
(단, 이 문제는 시간 복잡도
- 입력 조건
- 첫째 줄에 N과 x가 정수 형태로 공백으로 구분되어 입력된다. ( 1 ≤ N ≤ 1,000,000), (-10e9 ≤ x ≤ 10e9)
- 둘째 줄에 N개의 원소가 정수 형태로 공백으로 구분되어 입력된다. (-10e9 ≤ 각 원소의 값 ≤ 10e9)
- 출력 조건
- 수열의 원소 중 값이 x인 원소 개수를 출력한다. 단, 값이 x인 원소가 하나도 없다면 -1을 출력한다.
- 입력 예시
- 7 2
- 1 1 2 2 2 2 3
- 출력 예시
- 4
1) 문제 해결 아이디어
시간복잡도
특정 값이 등장하는 첫 번째 위치와 마지막 위치를 찾아 위치 차이를 계산하여 문제를 해결한다.
→ bisect_left(), bisect_right() 사용
2) Code
(1) Python
import sys
from bisect import bisect_left, bisect_right
fin = sys.stdin.readline
# 값이 [left_val, right_val]인 데이터의 개수를 반환
def count_by_range(array, left_val, right_val):
right_idx = bisect_right(array, right_val)
left_idx = bisect_left(array, left_val)
return right_idx - left_idx
n, x = map(int, fin().split())
array = list(map(int, fin().split()))
# 값이 [x, x] 범위에 있는 데이터의 개수 계산
count = count_by_range(array, x, x)
# 값이 x인 원소가 존재하지 않으면
if count == 0:
print(-1)
# 값이 x인 원소가 존재하면
else:
print(count)
parametric search에 대한 설명에서 충분히 설명하였으므로, 여기서는 생략한다.
(2) C++
#include <bits/stdc++.h>
using namespace std;
// 값이 [left_val, right_val]인 데이터의 개수를 반환
int countByRange(vector<int>& v, int leftVal, int rightVal) {
vector<int>::iterator rightIdx = upper_bound(v.begin(), v.end(), rightVal);
vector<int>::iteraotr leftIdx = lower_bound(v.begin(), v.end(), leftVal);
return rightIdx - leftIdx;
}
int n, x;
vector<int> v;
int main() {
// 데이터의 개수 N, 찾고자 하는 값 x 입력받기
cin >> n >> x;
// 전체 데이터 입력받기
for (int i = 0; i < n; i++) {
int temp;
cin >> temp;
v.push_back(temp);
}
count = counByRange(v, x, x)
if (count == 0) {
cout << -1 << endl;
}
else {
print(count)
}
파이썬의 bisect_left() 함수와 C++의 lower_bound() 함수,
파이썬의 bisect_right() 함수와 C++의 upper_bound() 함수는 완전히 똑같은 기능을 한다는 것을 알 수 있다.








최근댓글