나동빈님 유튜브의 '이것이 취업을 위한 코딩 테스트다' 강의와 교재 내용을 공부하고 그 내용을 정리해보자. (내용의 출처는 모두 유튜브 동빈나, 그리고 책 '이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 저'임을 사전에 밝힙니다.)
https://www.youtube.com/watch?v=2zjoKjt97vQ&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=2
목차
1. 그리디 알고리즘 개념
그리디 알고리즘(Greedy Algorithm)은 가장 기본적이지만 널리 사용되고 있는 알고리즘이다. 영단어 greedy의 단어 의미가 '탐욕적인' 이라는 의미를 갖고 있는 만큼, 탐욕법이라고 번역된다.
그리디 알고리즘은 현재 상황에서 지금 당장 가장 좋은 것을 선택하는 방법을 의미한다.
이후에 배우게 될 크러스컬 알고리즘이나 다익스트라 최단 경로 등과 같이 잘 알려진 알고리즘을 제외하고 일반적으로 그리디 알고리즘이 출제되면 해당 문제를 풀기 위한 최소한의 아이디어를 적절히 떠올릴 수 있어야 문제가 풀리도록 출제되는 경우가 많다.
그리디 알고리즘은 정당선 분석이 매우 중요하다. 단순히 현재 상황에서 가장 좋아 보이는 것을 반복적으로 선택하는 것이기 때문에, 그리디 알고리즘의 해가 항상 최적의 해라는 보장이 없다. 따라서 그리디 알고리즘을 사용해서 최적의 해를 선택할 수 있는지 검토하는 과정이 필요하다.
1) 그리디 알고리즘 예시
다음 예시를 통해 그리디 알고리즘을 이해해보자.
Q) 다음과 같이 하나의 그래프, 그 중에서도 트리가 구성되어 있다.
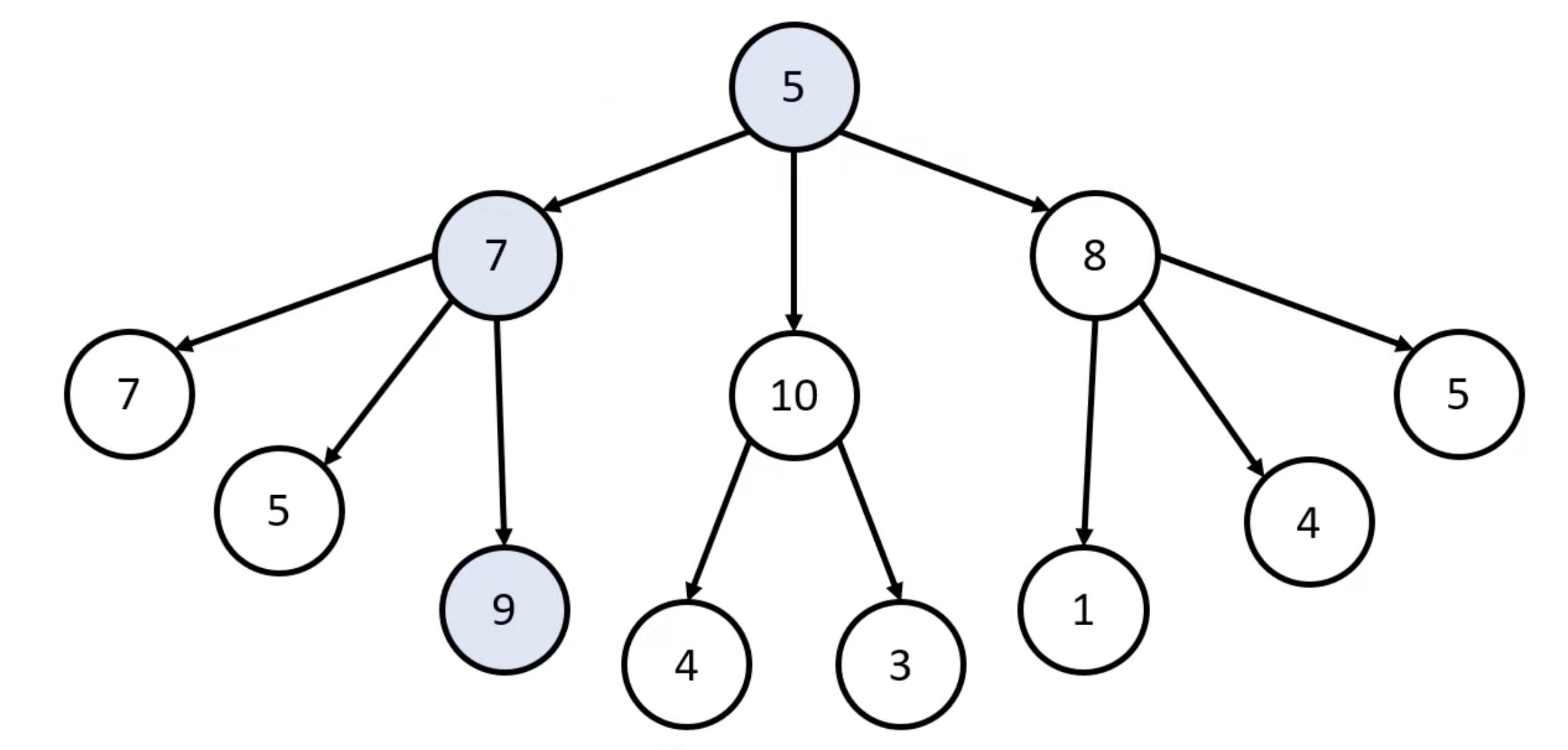
루트 노드인 5부터 출발하여 거쳐가는 노드의 값의 합을 최대로 만들고 싶을 때, 최적의 해는 무엇인가?
매우 간단한 구조이기 때문에 눈으로 보았을 때에도 파란색의 경로가 5+7+9 = 21로 최대의 경우임을 알 수 있다.
하지만, 그리디 알고리즘에서는 루트 노드 기준에서 가장 큰 값인 10, 다음 노드에서 가장 큰 값인 4로 진행하면서 5+10+4 = 19로, 최적의 값을 갖지 못한다.
이와 같이 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다. 실제 다양한 프로그램을 개발할 때에는 그리디 알고리즘을 사용하여도 충분히 최적의 해에 '가까운' 값을 얻을 수 있거나 혹은 최적의 해를 얻을 수 있는 경우가 많지만, 코딩테스트에서는 일반적으로 어떤 입력이 주어졌을 때, 어떤 출력이 나와야 한다는 것을 출제자가 정해두고 문제를 만들기 때문에 그리디 알고리즘이 최적의 해를 얻을 수 있다는 것을 추론할 수 있어야 한다. 즉, 그리디 알고리즘 문제가 출제된다면 이 알고리즘으로 얻은 해가 최적의 해가 되는 경우에 한해서 문제르 출제하는 경우가 많다.
2. 그리디 알고리즘 예제 - '거스름돈'
그리디 알고리즘의 대표적인 문제인 '거스름돈' 문제를 풀어보자.
Q) 당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 있다고 가정합니다. 손님에게 거슬루 주어야 할 돈이 N원일 때, 거슬러 주어야 할 동전의 최소 개수를 구하시오. 단, 거슬러 주어야 할 돈 N은 항상 10의 배수입니다.
1) 문제 해결 아이디어
먼저, 문제를 해결하기 위한 아이디어를 생각해보자.
- 최적의 해를 빠르게 구하기 위해서는 가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 좋을 것이다.
만약 N = 1260이라면, 가장 큰 화폐인 500원으로 가능한 만큼 거슬러 주면 2개, 100원은 2개, 50원 1개, 10원 1개가 된다.
2) 정당성 분석
다음으로, 이렇게 그리디 알고리즘을 사용하였을 때 최적의 해가 맞는지 정당성 분석을 해보아야 한다.
- 가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 최적의 해를 보장하는 이유는 무엇인가?
- 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로, 작은 단위의 동전들을 종합하여 다른 해가 나올 수 없다!
만약 800원을 거슬러 주어야 하는데, 화폐의 단위가 500원, 400원, 100원이라면, 그리디 알고리즘을 사용하였을 때에는 500원 1개 + 100원 3개 = 4개 라는 해가 도출되지만, 최적의 해는 400원 2개이다.
이는 500원짜리가 400원짜리의 배수가 아니기 때문에 400원짜리를 조합하여 더 최적인 해가 나올 수 있기 때문이다.
이처럼 그리디 알고리즘 문제에서는 문제 풀이를 위한 최소한의 아이디어를 떠올리고, 이것이 정당한지 검토하는 과정이 필요하다.
3) Code
Python, C++ 코드를 살펴보자.
(1) Python
n = 1260
count = 0
# 큰 단위의 화폐부터 차례대로 확인
array = [500, 100, 50, 10]
for coin in array:
count += n // coin # 해당 화폐로 거슬러 줄 수 있는 동전의 개수 세기
n %= coin
print(count)
(2) C++
#include <bits/stdc++.h>
using namespace std;
int n = 1260;
int cnt;
int coinTypes[4] = {500, 100, 50, 10};
int main(void) {
for (int i = 0; i < 4; i++) {
cnt += n / coinTypes[i];
n %= coinTypes[i];
}
cout << cnt << '\n';
}
4) 시간 복잡도 분석
화폐의 종류가 K개라고 할 때, 소스코드의 시간복잡도는 O(K)이다.
이 알고리즘의 시간 복잡도는 거슬러주어야 하는 금액 N과는 무관하며, 동전의 총 종류에만 영향을 받는다. 반복문이 화폐의 종류 만큼 실행되기 때문이다.
3. 그리디 알고리즘 예제 - '1이 될 때까지'
다음으로 '1이 될 때까지'라는 문제를 풀어보자.
Q) 어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행하려고 합니다. 단, 두 번째 연산은 N이 K로 나누어 떨어질 때만 선택할 수 있습니다.
- N에서 1을 뺍니다.
- N을 K로 나눕니다.
예를 들어 N이 17, K가 4라고 가정하면, 1번의 과정을 한 번 수행하면 N은 16이 됩니다. 이후에 2번의 과정을 두 번 수행하면 N은 1이 됩니다. 결과적으로 이 경우 전체 과정을 실행한 횟수는 3이 됩니다. 이는 N을 1로 만드는 최소 횟수입니다.
N과 K가 주어질 때, N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 최소 횟수를 구하는 프로그램을 작성하세요.
- 입력 조건 : 첫째 줄에 N(1 <= N <= 100,000)과 K(2 <= K <= 100,000)가 공백을 기준으로 하여 각각 자연수로 주어집니다.
- 출력 조건 : 첫째 줄에 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 횟수의 최솟값을 출력합니다.
- 입력 예시 : 25 5
- 출력 예시 : 2
1) 문제 해결 아이디어
나누기를 많이 수행할수록 총 연산 횟수가 줄어든다.
N의 값을 줄일 때 2 이상의 수 K로 나누는 작업이 1을 빼는 작업보다 연산 수를 훨씬 많이 줄일 수 있다.
따라서 나누어 떨어지는 경우 나누는 것을 우선적으로 하고, 나누어 떨어지지 않는 경우에는 1을 빼는 것으로 생각해볼 수 있다.
2) 정당성 분석
정당성 분석을 위해 가능하면 최대한 많이 나누는 작업이 최적의 해를 항상 보장할 수 있는지 생각해 보아야 한다.
문제의 조건에서 K는 항상 2 이상의 수이기 때문에 아무리 큰 수라고 해도 K로 나누기만 한다면 1을 빼는 것보다 기하급수적으로 빠르게 줄일 수 있다. 또한 N은 항상 1에 도달하여 최적의 해가 성립된다.
3) Code
Python, C++ 코드를 살펴보자.
(1) Python
# N, K를 공백을 기준으로 구분하여 입력 받기
n, k = map(int, input().split())
result = 0
while True:
# N이 K로 나누어 떨어지는 수가 될 때까지 빼기
target = (n // k) * k
result += (n - target)
n = target
# N이 K보다 작을 때 (더 이상 나눌 수 없을 때) 반복문 탈출
if n < k:
break
# K로 나누기
result += 1
n //= k
# 마지막으로 남은 수에 대하여 1씩 빼기
result += (n - 1)
print(result)
Technique
- target 변수 : n을 k로 나눈 몫에 다시 k를 곱한 값을 넣어 줌으로써 n이 k로 나누어 떨어지지 않는다고 했을 때 가장 가까운 k로 나누어 떨어지는 수가 어떤 건지 찾고자 할 때 사용할 수 있다.
- result 변수 : 총 연산을 실행하는 횟수라고 할 수 있는데, 1을 빼는 연산을 몇 번 수행할 지 한 번에 계산하여 대입해 주었다.
→ N과 K가 10만 이하의 정수이기 때문에 매번 N이 K로 나누어 떨어지는지 확인하는 방법으로 간단하게 코드를 작성할 수도 있지만, 위와 같은 방법으로 작성하면 한 번의 반복으로 바로 N이 K로 나누어지는 연산이 진행되기 때문에 반복 횟수에 따라 N이 기하급수적으로 빠르게 줄어든다.(log 복잡도를 가지게된다.)
(2) C++
#include <bits/stdc++.h>
using namespace std;
int n, k;
int result;
int main(void) {
cin >> n >> k;
while (true) {
// N이 K로 나누어 떨어지는 수가 될 때까지 빼기
int target = (n/k) * k;
n = target;
// N이 K보다 작을 때 (더 이상 나눌 수 없을 때) 반복문 탈출
if (n < k) break;
// K로 나누기
result++;
n /= k;
}
// 마지막으로 남은 수에 대해 1씩 빼기
result += (n - 1);
cout << result << '\n';
}
4. 그리디 알고리즘 예제 - '곱하기 혹은 더하기'
다음 예제를 살펴보자.
Q) 각 자리가 숫자(0부터 9)로만 이루어진 문자열 S가 주어졌을 때, 왼쪽에서 오른쪽으로 하나씩 모든 숫자를 확인하며 숫자 사이에 '×' 혹은 '+'연산자를 넣어 결과적으로 만들어질 수 있는 가장 큰 수를 구하는 프로그램을 작성하세요. 단, +보다 ×를 먼저 계산하는 일반적인 방식과는 달리, 모든 연산은 왼쪽에서부터 순서대로 이루어진다고 가정합니다.
예를 들어, 02984라는 문자열로 만들 수 있는 가장 큰 수는 ((((0+2) × 9) × 8) × 4) = 576입니다. 또한 만들어질 수 있는 가장 큰 수는 항상 20억 이하의 정수가 되도록 입력이 주어집니다.
- 입력 조건 : 첫째 줄에 여러 개의 숫자로 구성된 하나의 문자열 S가 주어집니다. (1 ≤ S의 길이 ≤ 20)
- 출력 조건 : 첫째 줄에 만들어질 수 있는 가장 큰 수를 출력합니다.
- 입력 예시 1 : 02984
- 출력 예시 1 : 576
- 입력 예시 2 : 567
- 출력 예시 2 : 210
1) 문제 해결 아이디어
대부분의 경우 '+'보다는 '×'가 더 값을 크게 만든다. 하지만 두 수중에 하나라도 '0' 혹은 '1'인 경우, 곱하기보다는 더하기를 수행하는 것이 더 효율적이다.
따라서 두 수에 대하여 연산을 수행할 때, 두 수 중에서 하나라도 1 이하인 경우에는 더하며, 두 수가 모두 2 이상인 경우에는 곱하면 된다.
2) Code
Python, C++ 코드를 살펴보자.
(1) Python
data = input()
# 첫 번째 문자를 숫자로 변경하여 대입
result = int(data[0])
for i in range(1, len(data)):
# 두 수 중에서 하나라도 '0' or '1'인 경우, 곱하기보다는 더하기 수행
num = int(data[i])
if num <= 1 or result <= 1:
result += num
else:
result *= num
print(result)
(2) C++
#include <bits/stdc++.h>
using namespace std;
string str;
int main(void) {
cin >> str;
// 첫 번째 문자를 숫자로 변경한 값을 대입
long long result = str[0] - '0';
for (int i = 0; i < str.size(); i++) {
// 두 수 중에서 하나라도 '0' 혹은 '1'인 경우, 곱하기보다는 더하기 수행
int num = str[i] - '0';
if (num <= 1 || result <= 1) result += num;
else result *= num;
}
cout << result << '\n';
}
5. 구현 개념
구현(Implementation)은 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정이다. 아무리 알고리즘을 잘 세워도 실제로 코드로 작성해서 프로그램으로 만들지 않으면 그 알고리즘이 실제로 동작하지 않을 것이다.
따라서 우리가 모든 알고리즘 문제를 푸는 과정에서 결국에는 구현이라는 과정을 거치게 된다.
하지만 일반적으로 특정 문제를 '구현 유형'의 문제라고 정의하는 경우는 대개 문제에서 요구하는 내용이 구현에 초점이 맞춰져 있거나 구현이 어려운 문제를 의미한다.
즉, 구현 유형의 문제란 풀이를 떠올리기는 쉽지만, 소스코드로 옮기기는 어려운 문제를 지칭한다.
구현 유형 문제의 예시는 다음과 같다.
- 알고리즘은 간단한데 코드가 지나칠 만큼 긴 문제
- 실수 연산을 다루고, 특정 소수점 자리까지 출력해야 하는 문제
- 문자열을 특정한 기준에 따라서 끊어 처리해야하는 문제 (파이썬이 편한 편!)
- 적절한 라이브러리를 찾아서 사용해야 하는 문제 (미리 적절한 라이브러리의 사용법을 알고 있어야 하고, 모른다면 구현을 직접 해야 해서 난이도가 매우 높아진다.)
이러한 문제들은 많은 연습이 필요한 분야이다. 많은 코드를 작성하고, 많은 라이브러리들의 존재와 사용법을 미리 안다면 당황하지 않고 구현 문제들을 해결할 수 있을 것이다.
교재에서는 시뮬레이션과 완전 탐색을 중점적으로 구현 유형 파트를 다룬다.
일반적으로 많은 기업의 코딩 테스트 문제에서는 2차원 공간에서의 처리를 요구한다. 실제로 2D 게임 개발 등을 할 때에는 이러한 2차원 공간을 행렬과 같은 형태로 표현하여 내부적으로 처리하는데, 실제 코딩테스트에서도 다양한 시뮬레이션 문제에서 이러한 2차원 공간을 가정하는 상황이 많이 등장한다.

예를 들어, '2차원 맵의 한 좌표에 등장하는 캐릭터가 반복적으로 어떤 위치로 이동한다'와 같은 문제 상황이 자주 등장한다. 이런 문제를 적절히 해결하기 위해서 행렬에 대한 이해가 필요하다.
행렬이란 2차원 데이터를 위 사진과 같이 표와 같은 형태로 쉽게 나타내는 수학 개념 중 하나인데, 프로그래밍 언어에서 2차원 배열이라고 부른다. (파이썬에서는 2차원 리스트)
사진에서 표의 가장 왼쪽, 위 부분이 첫 번째 원소(0번 원소)이고, 세로축을 행, 가로축을 열이라고 한다. 왼쪽에서 오른쪽으로 이동할수록 열 index가 증가하고, 위에서 아래로 이동할수록 행 index가 증가한다.
이는 중고등학교때 배운 유클리드 좌표계에서의 x축과 y축에 대한 개념과 방향이 조금 다르므로 유의하여야 한다.
또한 시뮬레이션 및 완전 탐색 문제에서는 2차원 공간에서의 방향 벡터가 자주 활용된다.

어떤 캐릭터나 사물 등이 특정 위치에 존재하다가 상하좌우로 이동한다 등의 상황이 전개되는 경우가 많은데, 이때 방향벡터를 사용한다.
예를들어, 만약 특정 위치에서 위로 이동한다면 행 데이터가 1만큼 감소한다. x는 행, y는 열을 의미하고, 동쪽을 예로 들자면 열만 1 증가하는 것이므로 dx[0] = 0, dy[0] = 1이 된다. (direction x, direction y)
6. 구현 예제 - 상하좌우
구현 문제 중에서 가장 대표적인 문제는 시뮬레이션 유형이다.
Q) 여행가 A는 N×N 크기의 정사각형 공간 위에 서 있다. 이 공간은 1×1 크기의 정사각형으로 나누어져 있으며, 가장 왼쪽 위 좌표는 (1, 1)이며, 가장 오른쪽 아래 좌표는 (N, N)에 해당한다. 여행가 A는 상, 하, 좌, 우 방향으로 이동할 수 있으며, 시작 좌표는 항상 (1, 1)이다. 우리 앞에는 여행자 A가 이동할 계획이 적힌 계획서가 놓여 있다. 이 계획서는 하나의 줄에 띄어쓰기를 기준으로 하여 L, R, U, D 중 하나의 문자가 반복적으로 적혀있으며, 각 문자의 의미는 다음과 같다.
- L : 왼쪽으로 한 칸 이동
- R : 오른쪽으로 한 칸 이동
- U : 위로 한 칸 이동
- D : 아래로 한 칸 이동
이때 여행가 A가 N×N 크기의 정사각형 공간을 벗어나는 움직임은 무시된다. 예를 들어 (1, 1)의 위치에서 L 혹은 U를 만나면 무시된다. 다음은 N=5인 지도와 계획서이다.
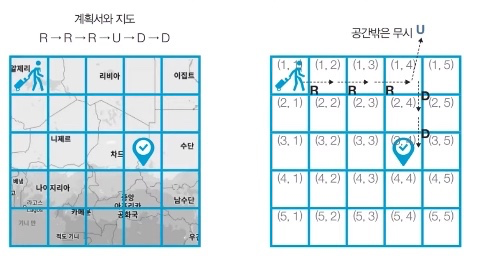
- 입력 조건
- 첫째 줄에 공간의 크기를 나타내는 N이 주어진다. (1 ≤ N ≤ 100)
- 둘째 줄에 여행가 A가 이동할 계획서 내용이 주어진다. (1 ≤ 이동횟수 ≤ 100)
- 출력 조건 : 첫째 줄에 여행가 A가 최종적으로 도착할 지점의 좌표 (X, Y)를 공백을 기준으로 구분하여 출력한다.
- 입력 예시 :
- 5
- R R R U D D
- 출력 예시 :
- 3 4
1) 문제 해결 아이디어
이 문제는 간단히 요구사항 대로 충실히 구현하면 되는 문제이다.
일련의 명령에 따라 개체를 차례대로 이동시킨다는 점에서 '시뮬레이션(Simulation)' 유형으로도 분류되며, 구현이 중요한 대표적인 문제이다. 다만, 알고리즘 교재나 문제 풀이 사이트에 따라 다르게 일컬을 수 있으므로, 코딩테스트에서의 시뮬레이션 유형, 구현 유형, 완전 탐색 유형은 서로 유사한 점이 많다는 정도로 기억해 두자.
2) Code
Python, C++ 코드를 살펴보자.
(1) Python
import sys
# N 입력 받기
n = int(sys.stdin.readline())
x, y = 1, 1
plans = list(map(str, sys.stdin.readline().rstrip().split()))
# L, R, U, D에 따른 이동 방향
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
move_types = ['L', 'R', 'U', 'D']
# 이동 계획을 하나씩 확인하기
for plan in plans:
# 이동 후 좌표 구하기
for i in range(len(move_types));
if plan == move_types[i]:
nx = x + dx[i]
ny = y + dy[i]
# 공간을 벗어나는 경우 무시
if nx < 1 or ny < 1 or nx > n or ny > n:
continue
# 이동 수행
x, y = nx, ny
print(x, y)
(2) C++
#include <bits/stdc++.h>
using namespace std;
int n;
string plans;
int x = 1, y = 1;
// L, R, U, D에 따른 이동 방향
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
char moveTypes[4] = {'L', 'R', 'U', 'D'};
int main(void) {
cin >> n;
cin.ignore(); // 버퍼 비우기
getline(cin, plans);
// 이동 계획을 하나씩 확인하기
for (int i = 0; i < plans.size(); i++) {
char plan = plans[i];
// 이동 후 좌표 구하기
int nx = -1, ny = -1;
for (int j = 0; j < 4; j++) {
if (plan == moveTypes[j]) {
nx = x + dx[j];
ny = y + dy[j];
}
}
// 공간을 벗어나는 경우 무시
if (nx < 1 || ny < 1 || nx > n || ny > n) continue;
// 이동 수행
x = nx;
y = ny;
}
cout << x << ' ' << y << endl;
return 0;
}
C++에서는 먼저 nx, ny를 초기화한 후, 반복문 안에서 이동 계획을 확인하여 nx, ny에 값을 실제 다음 위치 값으로 초기화하고 공간을 벗어나지 않을 때 x, y를 갱신시키는 방식으로 진행된다.
또한 C++, Java에서는 한 줄의 입력을 받기 위해서는 버퍼를 비워주어야 한다.
7. 구현 예제 - 시각
예제 하나를 더 풀어보자.
Q) 정수 N이 입력되면 00시 00분 00초부터 N시 59분 59초까지의 모든 시각 중에서 3이 하나라도 포함되는 모든 경우의 수를 구하는 프로그램을 작성하라. 예를 들어 1을 입력했을 때 다음은 3이 하나라도 포함되어 있으므로 세 주어야 한다.
- 00시 00분 03초
- 00시 13분 30초
반면 다음은 3이 하나도 포함되어 있지 않으므로 세면 안되는 시각이다.
- 00시 02분 55초
- 01시 27분 45초
- 입력 조건 : 첫째 줄에 정수 N이 입력된다. (0 ≤ N ≤ 23)
- 출력 조건 : 00시 00분 00초부터 N시 59분 59초까지의 모든 시각 중에서 3이 하나라도 포함되는 모든 경우의 수를 출력한다.
- 입력 예시 : 5
- 출력 예시 : 11475
1) 문제 해결 아이디어
이 문제는 가능한 모든 시각의 경우를 하나씩 모두 세서 풀 수 있는 문제이다. 하나씩 다 센다는 것은 가능한 경우의 수를 모두 검사해보는 탐색 방법이므로 전형적인 완전 탐색(Brute Forcing) 문제유형이라고 볼 수 있다.
하루는 86,400초이므로, 00시 00분 00초부터 23시 59분 59초까지의 모든 경우는 86,400가지이다. (24 * 60 * 60)
따라서 단순히 시간을 1씩 증가시키면서 3이 하나라도 포함되어 있는지를 확인하면 된다.
2) Code
Python, C++ 코드를 살펴보자.
(1) Python
import sys
finput = sys.stdin.readline
# H 입력 받기
h = int(finput())
count = 0
for i in range(h + 1):
for j in range(60):
for k in range(60):
# 매 시각 안에 '3'이 포함되어 있다면 카운트 증가
if '3' in str(i) + str(j) + str(k):
count += 1
print(count)
(2) C++
#include <bits/stdc++.h>
using namespace std;
int h, cnt;
// 특정한 시각 안에 '3'이 포함되어 있는지 여부
bool check(int h, int m, int s) {
if (h % 10 == 3 || m / 10 == 3 || m % 10 == 3 || s / 10 == 3 || s % 10 == 3)
return true;
return false;
}
int main(void) {
// H 입력 받기
cin >> h;
for (int i = 0; i <= h; i++) {
for (int j = 0; j < 60; j++) {
for (int k = 0; k < 60; k++) {
if (check(i, j, k)) cnt++;
}
}
}
cout << cnt << endl;
return 0;
}







최근댓글