인공지능을 위해 필요한 선형대수 내용을 간단하게 정리해보고자 한다.
4년간 배운 내용과 다른 블로그, 유튜브 등 여러 곳에서 조금씩 참고하여 정리했다.
전체적인 흐름은 유명한 '3Blue1Brown' 유튜브 채널의 선형대수 부분을 따랐다.
벡터 합, 벡터와 스칼라 곱, 행렬 합, 행렬 곱 등 기초적인 내용은 제외하고, 중요하면서도 외워둬야 할 것들 위주로 정리할 것이다.
목차
4. Determinant의 기하학적 의미
선형 변환을 하다보면 평면 또는 공간이 확장되거나 수축한다.
행렬식(Determinant)의 기하학적 의미는 2차원 평면에서 2 × 2 행렬 A에 의해 \(\hat{i}\), \(\hat{j}\)가 만드는 정사각형의 넓이의 증가율, 즉 선형 변환에 의한 영역의 변화를 나타내는 factor이다.
예를 들어, 행렬식이 3인 행렬에 의한 선형 변환으로 기존 영역은 3배가 되고, 행렬식이 1/2이면 기존 영역은 1/2배가 된다.
그렇다면 행렬식이 0이거나 음수일 때는 기하학적으로 어떻게 해석해야 할까?
먼저, 행렬식이 0일 때에는 (2 × 2 행렬 기준) 2차원 평면 공간이 1차원의 선이나 점으로 차원이 축소된다. (영역, 즉 넓이가 0이 됨)
동시에 이때에는 선형 변환 행렬의 column들이 linearly dependent할 것이다. (이전 포스팅 참고)
그리고 행렬식이 음수인 것은, 공간을 뒤집는 개념이다. 2 × 2 행렬 기준으로 평면을 뒤집으면서 영역의 넓이를 행렬식의 절댓값만큼 변화시킨다.
3차원에서는 평면에 대한 것을 공간으로 치환시켜 생각해주기만 하면 된다. (영역 → 부피)
(3차원 공간의 뒤집힘 → \(\hat{i}\), \(\hat{j}\), \(\hat{k}\) vector를 각각 검지, 중지, 엄지로 방향을 표현했을 때 오른손 법칙에서 왼손 법칙으로 바뀜)
이렇게 기하학적으로 이해하면, 아래 식도 쉽게 이해할 수 있다.
\(det(M_1 M_2) = det(M_1) det(M_2) \)
5. Inverse Matrices, Column Space, Null Space
1) 선형 방정식계 (System of Linear Equations)
선형 대수가 어떤 분야에서든 중요한 이유는, 선형 방정식계(system of (linear) equations)를 표현하기 쉽기 때문이다.
방정식계란, 미지수인 변수(unknown variables)와 관련된 식(equations)을 말한다.
선형 방정식 내에서 각 변수들의 역할은 어떤 상수를 스케일링하는 것이다. 식은 그것을 더한 값을 나타낼 뿐이다.
이러한 선형 방정식은 하나의 벡터방정식으로 간단하게 표현할 수 있다.
예를 들어, 다음과 같은 system of linear equations가 있다고 가정하면,
\(2x + 5y + 3z = -3\)
\(4x + 0y + 8z = 0 \)
\(1x + 3y + 0z = 2 \)
아래와 같은 벡터 방정식으로 나타낼 수 있다.
\( \begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -3 \\ 0 \\ 2 \end{bmatrix} \)
여기서 왼쪽의 상수 계수만을 모은 행렬을 계수 행렬 (Coefficient Matrix) (\(A\)), 변수를 모은 벡터를 변수 벡터 (Variable Vector) (\(\mathbf{x}\)), 우변의 상수를 모아둔 벡터를 상수 벡터(Constant Vector) (\(\mathbf{v}\))라 한다.
\(A \mathbf{x} = \mathbf{v} \)
이는 기하학적으로 봤을 때 선형변환행렬 A에 의해 벡터 v가 되는 벡터 x를 구하는 과정으로 볼 수 있다.
2) 역행렬(Inverse Matrix)
일단, determinant가 0이 아닌 경우, 즉 차원이 축소되지는 않는 경우를 살펴보자.
우리는 벡터 v를 알고 있으므로, 'x → v'가 아니라 벡터 v에서 역으로 선형 변환을 시켜주어 x를 찾아야 한다.
이때 A와 반대로 'v → x'로 선형 변환을 해주는 행렬을 역행렬(Inverse Matrix)이라 한다. (\(A^{-1}\)
따라서 \(A\)에 의한 선형 변환과 A의 역행렬 \(A^{-1}\)에 의한 선형 변환을 합성하면 처음 상태로 돌아간다.
이를 항등 변환(Identity Transformation)이라 하고, 이때의 행렬을 항등 행렬(Identity Matrix) \(I\)라 한다.
이에 따라 determinant가 0이 아닌 경우, 다음을 만족한다.
\(A^{-1} A = I \)
그럼 행렬식 값이 0이면 어떻게 될까?
행렬식 값이 0이면 선형 변환에 의해 차원이 줄어든다고 하였다. 그러면 줄어든 차원을 원래대로 되돌릴 '선형인' 변환은 없으므로, 행렬식 값이 0인 행렬은 역행렬이 존재하지 않는다.
하지만 \(A \mathbf{x} = \mathbf{v} \) 의 해는 존재할 수 있다.
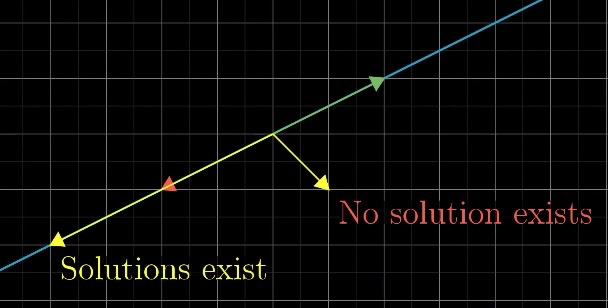
2차원이 행렬 A에 의해 아래와 같이 차원이 줄어들어 선이 되었다고 한다면, 해당 선상에 vector v가 존재하면 해가 무수히 많아진다.
하지만 선을 벗어난 방향으로 v가 존재하면 해가 없다. (원점 → 자명한 해, 무시)
3) 계수(Rank)
3 × 3 행렬의 행렬식이 0인 경우, 변환의 결과가 여러가지로 나뉜다. 2차원(평면)으로 줄어들거나, 1차원(선)으로 줄어들거나, 점으로 줄어들거나.
따라서 단순히 행렬식이 0이라는 표현보다 정확한 구분이 필요한데, 이때 사용되는 개념이 바로 계수(Rank)이다.
즉, Rank는 변환 결과의 차원의 수를 말한다.
- 선형 변환 행렬에 의한 변환 결과가 1차원(선)이면 Rank는 1이다.
- 선형 변환 행렬에 의한 변환 결과가 2차원(평면)이면 Rank는 2이다.
따라서 2 × 2 행렬의 최대 rank는 2, 3 × 3 행렬의 최대 rank는 3이다. 이는 곧 행렬식 값이 0이 아님을 말한다. (full rank)
그리고, 이렇게 행렬의 가능한 결과(선, 평면, 공간 등)의 집합을 그 행렬의 'Column space'라 한다.
행렬의 열들은 기저벡터의 변환 후의 좌표를 말한다. 예를 들어, 선형 변환 행렬 \(A\)가 아래와 같다면,
\( \begin{bmatrix} 3 & 1 \\ 4 & 1 \end{bmatrix} \)
\(\hat{i} = [3 4]^T\)이고, \(\hat{j} = [1 1]^T\)이다.
이러한 변환 후 기저벡터들의 'span'은 가능한 모든 결과 공간을 알려준다.
다시말해, 열 공간(Column Space)이란, 행렬의 열들의 span이다.
따라서, Rank의 정확한 정의는 이러한 Column Space의 차원 수이다.
3) 영공간(Null Space, Kernel)
참고로, 영벡터는 어느 열공간이든 포함되어있다. 선형 변환은 원점이 항상 고정되어야 하기 때문이다.
그런데 행렬식이 0인 행렬에 의해 차원이 축소되면, 축소되기 이전에 다른 점으로 나타나던 여러 벡터의 집합(선 또는 평면)들이 원점으로 축소된다.
예를 들어, 2차원에서 1차원으로 줄어드는 행렬에 의해 다음과 같이 선이 원점으로 축소된다.
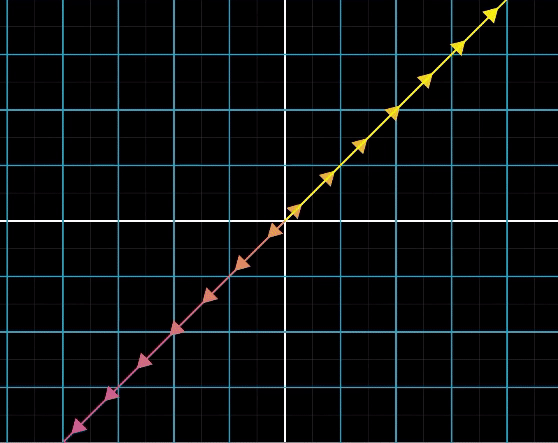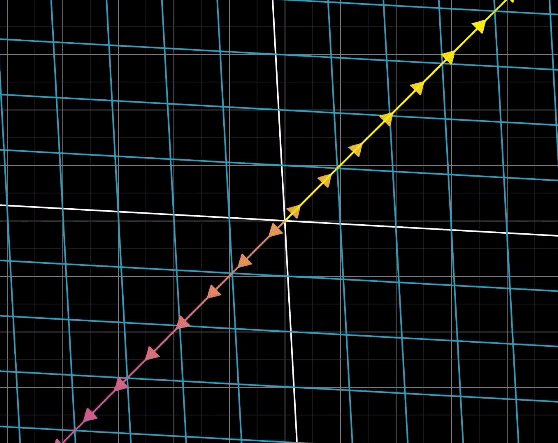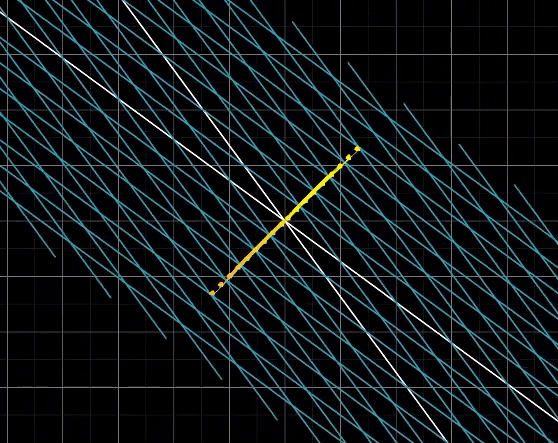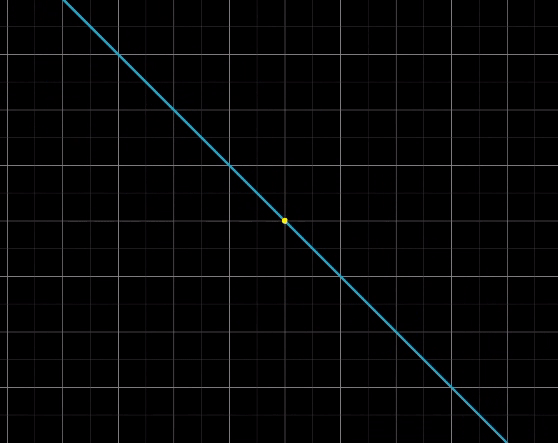
그리고 3차원에서 2차원으로 줄어들 때에도 다음과 같이 선이 원점으로 축소된다.
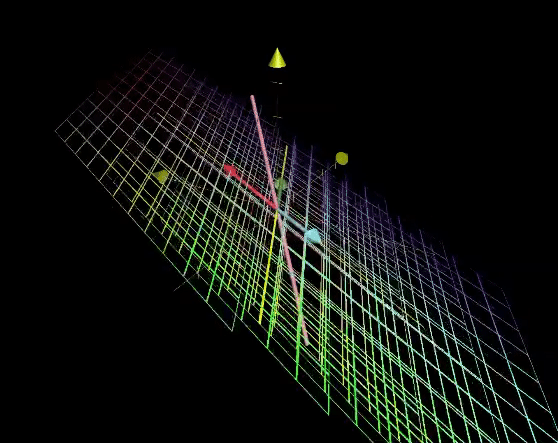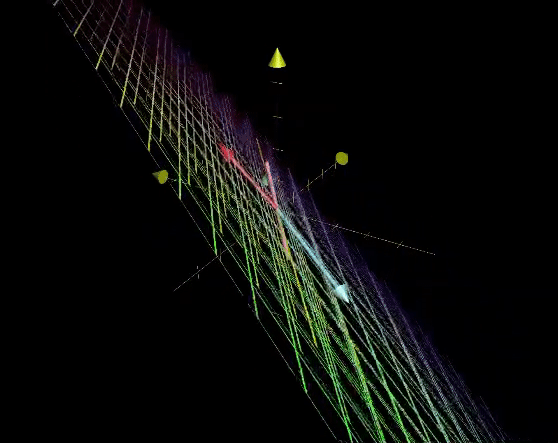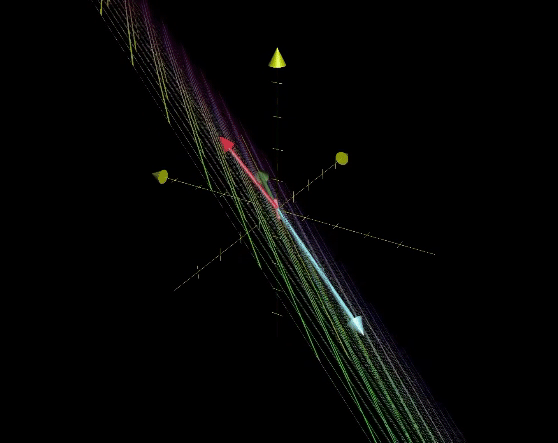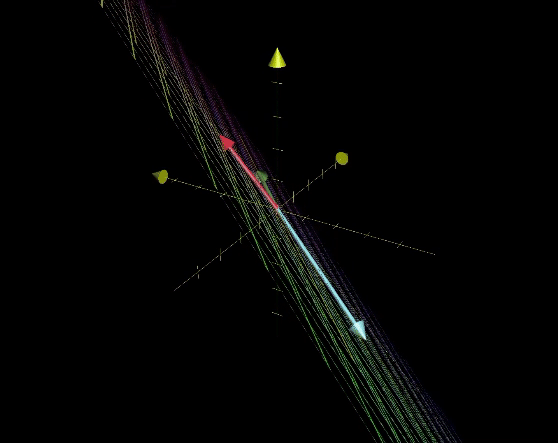
그런데, 3차원에서 1차원으로 차원이 2개 줄어들면, 평면이 원점으로 축소된다.

이와 같이, 원점으로 이동되는 벡터들의 집합을 그 행렬의 Null Space 혹은 Kernel이라고 한다.







최근댓글