통계학은 인공지능과 겹치는 부분이 매우 많고, 쉬운 개념도 잊기 쉽다.
매우 기초적인 지식은 알고 있다고 가정하고, 머신러닝을 수행하기 위한 내용을 공부해보자.
학부 과정에서 배운 확률과 통계, 데이터마이닝 내용과 책 'Mathematics for Machine Learning'을 참고했다.
목차
5. 확률 변수의 기댓값(Expected Value) 및 분산(Variance)
기댓값과 분산은 앞선 포스팅에서 평균과 분산을 설명할 때 말했듯이, 데이터를 표현하기 위해 중요한 값이다.
기댓값(Expected Value,
이는 마치 어떤 확률적 사건에 대한 평균, 특히 '모평균'의 의미로 사용될 수 있다.
또한 분산(Variance,
1) Expected Values of Discrete/Continuous Random Variable
Discrete random variable
Continuous random variable
2) Expected Values of PMF/PDF
먼저, 확률변수
마찬가지로, 확률변수
여기서,
따라서 다음과 같은 기댓값 관련 정리를 얻을 수 있다.
- 역은 성립하지 않음에 주의해야 한다.
3) Variances of Random Variable
확률 변수의 분산은 다음과 같의 정의한다.
또한, 확률 변수가 두 개 이상인 경우, 공분산(Covariance)과 상관 계수(Correlation Coefficient)에 대한 개념을 알고 있어야 한다.
Covariance란, 두 변수가 함께 변하는 정도, 경향성을 나타낸다.
하지만 variance와 covariance는 단위 변화 (scale 변화)에 영향을 받기 때문에 두 값 사이의 관계를 온전히 나타내지는 못한다.
따라서 두 변수간의 관계를 scale의 영향 없이 나타내기 위해 도입한 개념이 correlation coefficient이다.
분산이
두 확률 변수
참고로,
또한 correlation coefficient 중 가장 기본적인 Pearson's Correlation Coefficient
(sample correlation coefficient는 생략한다.)
식에서 알 수 있듯이, covariance에 각각의 standard deviation을 나누어주면서 scale의 영향을 없앴다.
분산 관련 정리는 다음과 같다.
- 기댓값에서는 곱셈, 분산에서는 덧셈임에 유의하자.
6. Sum Rule, Product Rule, Bayes' Theorem
이제까지 배운 내용을 좀 더 일반적으로 표현해보자.
이때 marginal probability, conditional probability의 정의에 따라 확률 이론에서의 기초적인 규칙을 알 수 있다.
0) Probability vs Likelihood
먼저 probability와 likelihood의 개념에 대해 간단히 정리하고 넘어가자.
이는 차후에 정리하게 될 'Maximum Likelihood Estimation' 부분에서도 다룰 것이며, Youtube 'StatQuest'의 내용을 참고했다.
확률과 우도는 공통적으로 어떤 일이 일어남직한 정도를 말한다.
비슷한 개념을 나타내므로 헷갈리기 쉬운데, 어떤 차이점이 있는지 알아보자.
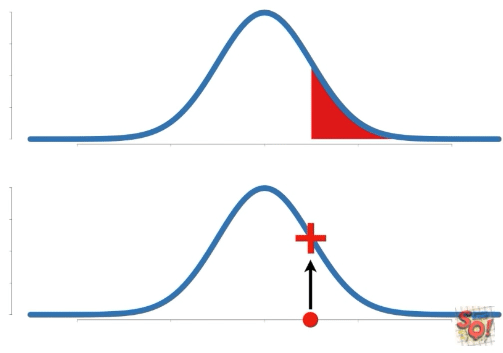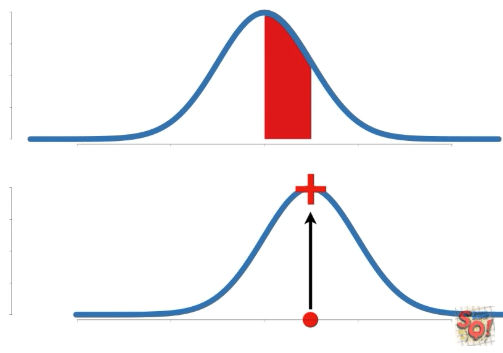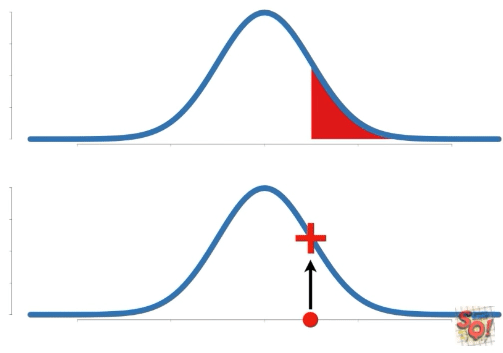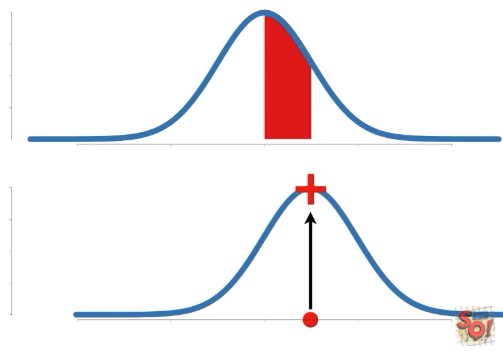
Probability는 고정된 확률 분포에 대한 특정 구간의 넓이를 말한다. 따라서 구하는 data의 구간이 바뀐다.
이에 비해 Likelihood는 고정된 data point(s)에 대한 확률 분포 상의 y축 값을 말한다. 따라서 확률 분포가 변함에 따라 값이 바뀐다.
1) sum rule
첫 번째 rule은 sum rule (또는 marginalization property)이다.
이때 ,
이 규칙은 joint distribution을 marginal distribution과 연관짓는다.
일반적으로, 3개 이상의 확률 변수를 갖는 joint distribution에서, sum rule은 random variable의 특정 subset에 적용될 수 있다.
확률 변수 벡터
'
2) product rule
다음으로, product rule을 살펴보자.
이는 joint distribution을 conditional distribution과 관련시키는데, 그 방법은 아래 수식과 같다.
이는 확률 변수 두 개에 대한 모든 joint distribution이 다른 두 distribution의 곱으로 표현된다는 것을 의미한다.
교집합에 대해서는 순서를 바꾸어도 상관 없으므로,
3) Bayes' theorem
Bayes' theorem은 Bayes' rule 또는 Bayes' law로 불리기도 한다.
머신러닝과 Bayesian 통계학에서는 관측된 random variable로부터 관측되지 않은 random variable의 추론을 하려 한다.
즉, 기존 통계학에서는 확률 공간을 엄격히 정의하여 집단의 분포를 정의했고, 계산을 통해 파생되는 결과물을 수용(연역적 사고)했지만, 베이지안 관점의 통계학에서는 prior 등 경험적이고, 불확실성을 내포하는 수치를 기반으로 하여 추가 정보를 통해 posterior을 갱신(귀납적, 경험적 추론)한다.
이런 점에서 Bayes' theorem은 'probabilistic inverse'라고 불리기도 한다.
관측되지 않은 random variable
각 항을 자세히 살펴보자.
- prior
- 개념적으로 prior knowledge를 나타내며, 0이 아닌지 꼭 확인해야 한다.
- likelihood
- "likelihood of
- "likelihood of
- posterior
- evidence
- posterior의 normalization을 입증한다.
- integration 때문에 계산이 복잡하다.
product rule로 쉽게 증명할 수 있다.








최근댓글